写力扣第五题引发的manacher算法

题目是给定一个字符串s，找到最长回文子串

最早就是暴力查找，两个指针截取字符s的一部分，在对这部分进行检测，是否符合回文数字的，是的话就更新最大值，然后记录每次最大值的起始位置，输出截取即可，但是这样的时间复杂度太高。

就在网上看到别人讲解一种和KMP算法类似的一种算法，马拉车算法，赶紧来学习一下。

首先是想到一种由中心向两边扩张，检查两边的字符是否相等，这个方法可以检查到每一个字符以自己为中心得到的两边的最长子串，但是他设计奇数偶数的问题，设想abba的情况，检测到a了，为1（本身也是一个回文数），b的时候两边不相等，为1，b（第二个）又是1，a又是1，其实不然，他应该是回文数的如果是奇数的情况是aba就好办多了，检测到b的时候，两边相等+2，就等于三了更新了最大值，于是就有了在每个字符边都新增一个字符，

abba-->#a#b#b#a# 

考虑一个问题 加入的字符有没有必要和字符串中的字符避免重复？

其实是不用的，因为我们是这样对于当前的字符，同时向两边扩的，如果当时左边的是新增的，右边一定是新增的，并且相等。

然后我们先引入一个概念，就是最大回文直径，和中心点

最大回文直径也就是从当前遍历的这个点，左右开始查找，所找到的最大长度；

设想某一个左右不相等那么他就是1（本身这个元素），左右符合了，一次增加两个长度

每次查找完成都要记得更新最大值，并保存最大值对应的圆心，主要是用于字符截取

是这样截取的，记录中间点，左右都是长度的一半。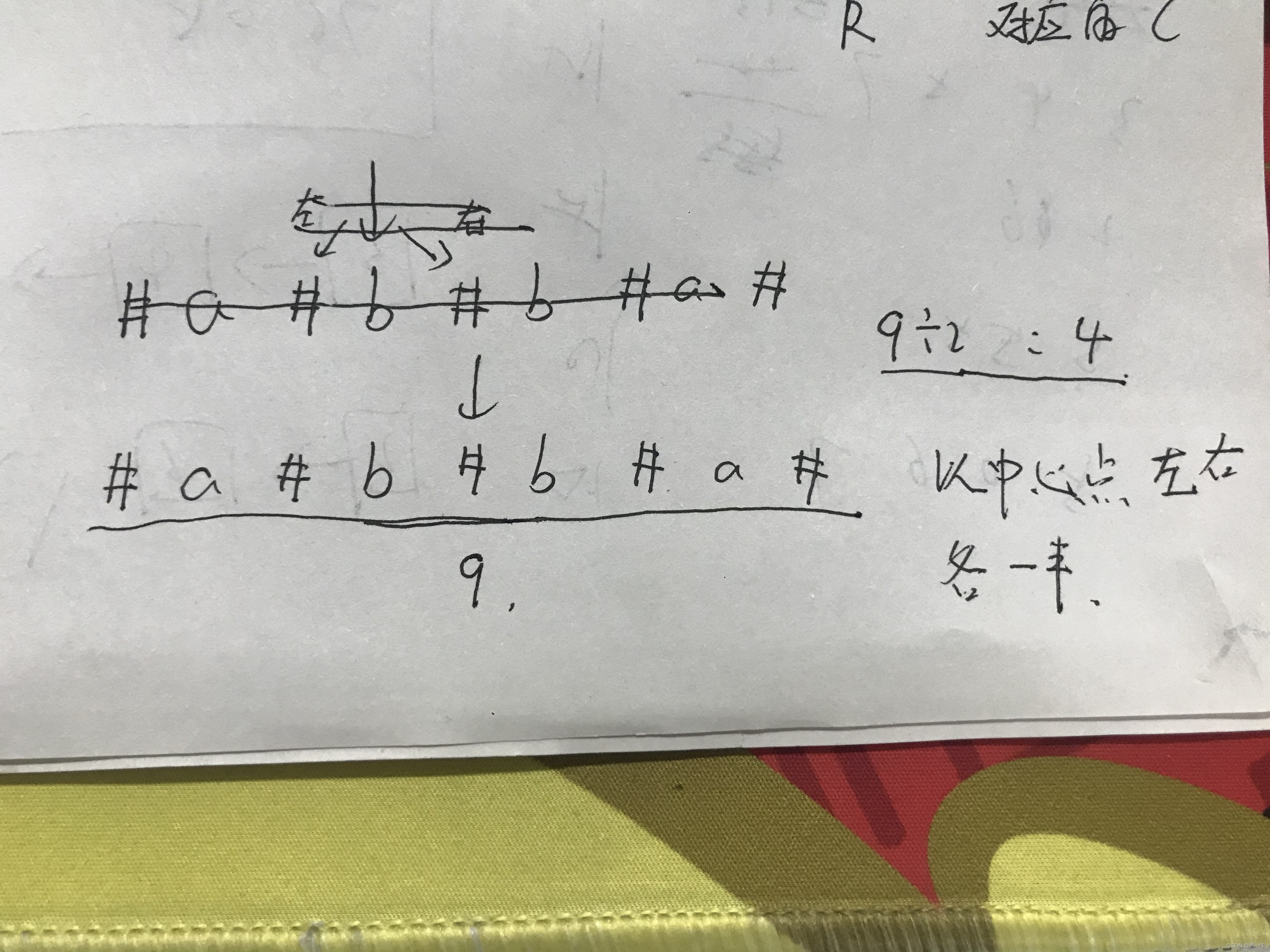

 如果查找过程中，有一个数的长度是等于了这个字符串的长度，那就不用再查找了，因为这个串本身就是了。

先处理这个字符串

        char []sa=s.toCharArray();
        char []sb=new char[s.length()*2+1];
        int in=0;
        for (int i = 0; i < sb.length; i++) {
            if(i%2==0){
               sb[i]='#';
            }
            else{
           sb[i]=sa[in];
in++;
            }
        }

然后开始遍历这个字符数组

        int max=1;//默认当前的最大值
        int max_index=0;//取得最大值的那个位置
        for (int i = 0; i < sb.length; i++) {
            int l=i-1,r=i+1,curMax=1;//左右指针扩张 临时最大值记录
            while(l>=0 && r<sb.length){
                if(sb[l]==sb[r]){
                    curMax+=2;
                    l--;
                    r++;
                }
                else break;
            }
            if(curMax>max){//大了就更新最大值
                max=curMax;
                max_index=i;
            }
            if(max==sb.length) {//这种情况是 不用再查找了
                break;
        }
    }

最后就得到max与max的下表max_index这两个数字

然后对字符数组截取

    String  ssb=new String(sb);
    String ans=ssb.substring(max_index-max/2,max_index+max/2);
    ans.replaceAll("#", "");