队列、栈、链表和滤波算法

队列

队列典型用例：单片机AD采样往队列中填充采样值。

存储数据的方式：
1、用for循环直接下标+1，将整体往左平移一位。
2、直接用新的采样值替换要丢弃的采样值，记录要丢弃值的下标，形成环形队列。

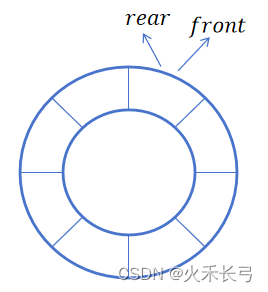
在初始化创建空队列时，令front = rear = 0，每当插入新的队列尾元素时，尾指针rear增1；每当删除队列头元素时，头指针front增1。因此，在非空队列中，头指针始终指向队列头元素，而尾指针始终指向队列尾元素的下一个位置。（所以满的环形队列通常会预留一个位置，如果不预留，会导致front = rear，导致判空和判满的条件重合）

环形队列思路：

（1）front/rear初始值：front就指向队列的第一个元素，rear指向队列最后一个位置的后一个元素，front = rear = 0；
（2）队列判满条件：(rear + 1) % maxSize = front；
（3）队列判空条件：front = rear；
（4）队列有效数据个数：(rear + maxSize - front) % maxSize。

入队、出队、判满、判空（环形队列无插队函数）

#include <stdio.h>
#include <assert.h>
#include <Windows.h>

#define MaxSize 10  //队列的最大容量

typedef int DataType;  //队列中元素类型#define 定义的名字在预处理时即被丢弃；而typedef定义的名字一直在调试器中可见，可以在调试代码时使用
typedef struct Queue
{
    DataType Queue[MaxSize];
    int fornt;   //队头指针
    int rear;    //队尾指针
}SeqQueue;

//队列初始化，将队列初始化为空队列
void InitQueue(SeqQueue *SQ)
{
    SQ->fornt = SQ->rear = 0;  //把对头和队尾指针同时置0
 }

//判断队列为空
int IsEmpty(SeqQueue* SQ)
{
    if (SQ->fornt == SQ->rear)
    {
        return 1;
    }
    return 0;
}

//判断队列是否为满
int IsFull(SeqQueue* SQ)
{
    if (SQ->rear == MaxSize) 
    {
        return 1;
    }
    return 0;
}

//入队,将元素data插入到队列SQ中
void EnterQueue(SeqQueue* SQ,DataType data)
{
    if (IsFull(SQ))
    {
        printf("队列已满\n");
        return 0;
    }
    SQ->Queue[SQ->rear] = data;  //在队尾插入元素data
    SQ->rear = SQ->rear + 1;     //队尾指针后移一位
}

//出队，将队列中队头的元素data出队，出队后队头指针front后移一位
int DeleteQueue(SeqQueue* SQ,DataType* data)
{
    if (IsEmpty(SQ))
    {
        printf("队列为空！\n");
        return 0;
    }
    *data = SQ->Queue[SQ->fornt];   //出队元素值
    SQ->fornt = (SQ->fornt)+1;      //队尾指针后移一位
    return 1;
}

//获取队首元素
int GetHead(SeqQueue* SQ,DataType* data)
{
    if (IsEmpty(SQ))
    {
        printf("队列为空!\n");
    }
    return *data = SQ->Queue[SQ->fornt];  
}

//清空队列
void ClearQueue(SeqQueue* SQ)
{
    SQ->fornt = SQ->rear = 0;
}

//打印队列中的与元素
void PrintQueue(SeqQueue* SQ)
{
    assert(SQ);    
    int i = SQ->fornt;
    while(i<SQ->rear)
    {
        printf("%-3d", SQ->Queue[i]);
        i++;
    }
    printf("\n");
}

滤波算法

限幅滤波
a.对当前值范围进行最大限幅
b.对相邻值之间的偏差进行最大限幅
根据经验判断，确定两次采用允许的最大偏差值（设为A），每次检测到新值时判断：
优点：可以有效的克服因偶然因素而引起的脉冲干扰；
缺点：不能抑制周期性的干扰；平滑度较差。

/*对当前值范围进行最大限幅*/
float maxFilter(float input,float MAX)
{
   static float lastValue = 0;
   if ( ( input > MAX ) || (input < -MAX ))
	 {
      return lastValue;
	 }
	 lastValue = input;
   return input;
}

/*对相邻值之间的偏差进行最大限幅*/
#define DELAT_MAX 10
// 定义滤波数据类型
typedef	int filter_type;
filter_type filter(filter_type effective_value, filter_type new_value, filter_type delat_max)
{
	if ( ( new_value - effective_value > delat_max ) || ( effective_value - new_value > delat_max ))
		return effective_value;
	return new_value;
}

递推均值滤波
把连续N个采样值看成一个队列，队列的长度固定为N，每次采样到一个新数据放入队尾，并扔掉原来队首的一次数据（先进先出原则）把队列中的N个数据进行算术平均运算，就可以获得新的滤波结果。（例如单片机AD采样）
优点： 对周期性干扰有良好的抑制作用，平滑度高，适用于高频振荡的系统
缺点： 不易于消除干扰所引起的采样值偏差，不适用于脉冲干扰比较严重的场合；
涉及到队列，比较浪费RAM，ROM(它和限幅滤波器的优缺点正好相反）。不适用于对要求数据计算速度较快或测量速度较慢的实时控制。

/*递推均值滤波*/
#define num_size 50
typedef struct
{
	double Filter_Buffer[num_size];
	uint16_t id;
	double sum;
	double average; 
}Mean_Filter;
void Mean(Mean_Filter *filter, double Data)
{
	filter -> sum -= filter -> Filter_Buffer[filter -> id];  //减去最旧的数
	filter -> sum += Data;                                  //加进最新的数
	filter -> Filter_Buffer[filter -> id] = Data;           //将最新的数覆盖最旧的数
	filter -> average = filter -> sum/num_size;
	if(++filter->id == num_size)
	{
		filter -> id = 0;
	}
}
while(1)
{
	Data = rand()/(double)RAND_MAX;
	Data += i;
	Mean(&Example_struct, Data);
	printf("%f, %f", Data, Example_struct.average);
	Delay25ms();
}

中值滤波算法
连续采样n次（一般取奇数），把n次采样值按大小排列，形成有序数据，取中间值为本次有效值。
优点：它能有效克服因偶然因素引起的波动干扰，对温度、液位等变化缓慢的被测参数有良好的滤波效果
缺点：但是对流量、速度等快速变化的参数滤波效果较差。

unsigned char GetMedianNum(int * bArray, int iFilterLen)
{
	int i,j;// 循环变量
	unsigned char bTemp;
	
	// 用冒泡法对数组进行排序
	for (j = 0; j < iFilterLen - 1; j ++)
	{
		for (i = 0; i < iFilterLen - j - 1; i ++)
		{
			if (bArray[i] > bArray[i + 1])
			{
				// 互换
				bTemp = bArray[i];
				bArray[i] = bArray[i + 1];
				bArray[i + 1] = bTemp;
			}
		}
	}
	
	// 计算中值
	if ((iFilterLen & 1) > 0)
	{
		// 数组有奇数个元素，返回中间一个元素
		bTemp = bArray[(iFilterLen + 1) / 2];
	}
	else
	{
		// 数组有偶数个元素，返回中间两个元素平均值
		bTemp = (bArray[iFilterLen / 2] + bArray[iFilterLen / 2 + 1]) / 2;
	}

	return bTemp;
}

栈

栈的典型用例

函数的层层调用类似于入栈，函数的层层退出类似于出栈。

栈的存储方式：
a、顺序存储
b、链式存储

栈和堆的区别：
栈（stack）：由编译器自动分配释放
堆（heap）：一般由程序员分配和翻放

int a = 0;
char *p1;
void main(void){
	int b; //栈
	char s[] = "abc"; //栈
	char *p2; //栈
	char *p3 = "123456"; //123456\0在常量区，p3在栈上
	static int c = 0; //全局（静态）初始化区
	p1 = (char *)malloc(10); //堆
	p2 = (char *)malloc(20); //堆
}

/*顺序存储结构*/
#define MaxSize 100  //定义栈中元素的最大个数
typedef struct SqStack{
	int data[MaxSize];
	int top;
}SqStack;

/*链式存储结构*/
typedef struct LinkNode{
	int data;  //数据域
	struct LinkNode *next;  //指针域
}*LiStack;

栈的基本操作包括：
初始化InitStack(&S);
判空Empty(S);
进栈Push(&S, x);
出栈Pop(&S, &x);
读栈顶元素GetTop(S);
遍历栈PrintStack(&S);
销毁栈DestroyStack(&S);
[注]以上操作均采用顺序栈来实现。

//初始化
void InitStack(SqStack &S){
    S.top = -1;
}

//判栈空
bool Empty(SqStack S){
    if(S.top == -1){
        return true;
    }else{
        return false;
    }
}

//入栈
void Push(SqStack &S, int x){
    if(S.top == MaxSize-1){
        printf("栈满");
        return;
    }
    S.data[++S.top] = x; //指针先加一，再入栈
}

//出栈
void Pop(SqStack &S, int &x){
    if(S.top == -1){
        printf("栈空");
        return;
    }
    x = S.data[S.top--]; //先出栈，指针再减一
}

//读栈顶元素
int GetTop(SqStack S){
    if(S.top == -1){
        printf("栈空");
        return -1;
    }else{
        return S.data[S.top];
    }
}

//销毁栈
void DestroyStack(SqStack &S){
    S.top = -1;
}

链表

链表典型用例：在RTOS中，可以使用链表来管理定时器事件。每个定时器表示为一个节点，通过链表的方式遍历、添加和删除定时器。

链表和队列、栈最大的区别是它不需要连续的存储区域，是一种没有顺序的存储结构。

链表包括两个部分：1、存储数据元素的节点的数据域，2、指向下一节点的指针的指针域。

优点：和纯属表顺序结构相比，链表结构插入、删除操作不需要移动所有节点，不需要初始化容量。
缺点：搜索时必须遍历节点，需要更大的运行空间。

//创建链表
typedef struct Node{
    int data;
    struct  Node *next;
}SNode,*Linkist;

一般创建链表会使用typedef struct，因为这样定义结构体变量时，就可以直接可以用LinkList *a;定义结构体类型变量了。

Linkist CreateNode(){
    int num;
    int i=1;
    Linkist L;
    Linkist p,r;
    L=(SNode *)malloc(sizeof(SNode));
    L->next=NULL;//初始化
    p=L;
    printf("please input %d number:(数字0结束输入)\n",i);
    scanf("%d",&num);
    while(num!=0){
        i=i+1;
        r=(SNode *)malloc(sizeof(SNode));
        r->data=num;
        r->next=NULL;
        p->next=r;
        p=r;
        printf("please input %d number:\n",i);
        scanf("%d",&num);
    }
    return L;

打印链表

void PrintList(Linkist L){
    Linkist P;
    P=L->next; // P 指向链表头节点的下一个节点，这里假设头节点的 next 指针指向了第一个有效节点。
    printf("\n建立的单链表为：\n");
    while(P!=NULL){
            printf("%d\n",P->data);
            P=P->next;
    }
}

int main()
{
    Linkist T;
    T=CreateNode();
    PrintList(T);
    change(T, 3);
    return 0;
}

修改链表节点值

修改链表节点值很简单。下面是一个传入链表和要修改的节点，来修改值的函数。

Linkist change(Linkist L,int n) {//n为第n个节点
    int num;
	Linkist H, X;
	H=L->next;
    int i = 0;
	while (i < n && H != NULL) {
		H = H->next;
		i++;
	}
	if (H != NULL) {
		puts("输入要修改的值");
		scanf("%d", &num);
        X=H->next;
        H->data=num;
        H->next=X;
	}
	else {
		puts("节点不存在");
	}
    return L;
}

删除链表中的节点

Linkist Delete(Linkist L, int n){
	Linkist H, temp1, temp2;
	H=L->next;
	int i = 0;
	while(i < n-1 && H != NULL){
		H=H->next;
		i++;
	}
	temp1=H->next;
	if(temp1 != NULL){
		temp2=temp1->next;
		H->next=temp2;
	}
	return L;
}