深度学习_01_基础知识

神经网络模型

1.人工神经网络

人工神经网络：

大量的神经元以某种连接方式构成的机器学习模型。

模型：M-P模型

公式：

$y=f(\sum _{i=1}^n{I}_i{w}_i)$

参数：

$I_i:$ 输入的样本数据
$w_i:$ 权重
$f:$ 激活函数
$y:$ 输出数据

2.感知机：

感知机：

Percepttron(感知机)是第一个神经网络

模型：

公式：

$O=\sigma (<w,x>+b)$
$\sigma =\{\begin{array}{l}1,x>0\\ \\ 0,otherwise\end{array}$

参数：

$O:$输出数据
$\sigma :$ 激活函数
$w:$权重
$x:$输入数据
$b:$bias,偏置

多层感知机

多层感知机：

在单层神经网络基础上引入一个或多个隐藏层，使神经网络有多个网络层。

1.多层感知机的前向传播

模型图：

公式：

$H_{1\times 5}=\sigma (X_{1\times 4}\cdot W_{h(4\times 5)})$
$O_{1\times 3}=\sigma (H_{1\times 5}\cdot W_{o(5\times 3)})$

参数：

$H_{1\times 5}:$ 隐藏层的输出
$X_{1\times 4}:$ 输入数据（将输入数据组合成一个1×5的矩阵）
$W_{5\times 3}:$ 权重矩阵
$O_{1\times 3}:$ 输出数据（最后输出一个1×3的矩阵）

2.多层感知机的激活函数

此处主要是为了证明激活函数的意义！---->加入激活函数可避免网络退化为单层网络
模型图：

公式推导：

$H=X{W}_h+b_h$ ---->隐藏层的输出
$O=H{W}_o+b_o$ ---->输出层的输出
$O=X{W}_b{W}_o+b_o=X{W}_h{W}_o+b_o$
由于$W_h和W_o$可以看成一个整体$W$,所以网络退化成单层网络了！

激活函数

激活函数的作用：

激活函数的性质：

激活函数的类型：

目前最常用的激活函数为ReLu激活函数，因为sigmoid函数和Tanh激活函数存在饱和区，从而使梯度接近零，导致在反向传播过程中梯度变化非常小，使得权重更新缓慢，，网络难以学习。

反向传播算法

链式求导法则：

$$y=f(u),u=g(x)$$
$$\frac{\partial y}{\partial x}=\frac{\partial y}{\partial u}\frac{\partial u}{\partial x}$$

1. 前向传播：

输入层数据（样本X数据）开始从前往后，数据逐步传输到输出层

1-2.前向传播公式推导：

$$z=x\cdot W^1$$.
$$h=\varphi (z)$$
$$O=h\cdot W^2$$

2.反向传播：

反向传播： 损失函数开始从后向前，梯度逐步传输至第一层

2-1.网络计算图

公式推导：

$$\frac{\partial L}{\partial W^2}=prod(\frac{\partial L}{\partial O},\frac{\partial O}{\partial W^2})=\frac{\partial L}{\partial O}\cdot h^T$$
$$\frac{\partial L}{\partial h}=prod(\frac{\partial L}{\partial O},\frac{\partial O}{\partial h})=W^T$$
$$\frac{\partial L}{\partial z}=prod(\frac{\partial L}{\partial O},\frac{\partial O}{\partial h},\frac{\partial h}{\partial z})=\frac{\partial L}{\partial h}\cdot \varphi (z{)}^{\prime }$$
$$\frac{\partial L}{\partial W^2}=prod(\frac{\partial L}{\partial O},\frac{\partial O}{\partial h},\frac{\partial h}{\partial z},\frac{\partial z}{\partial W^2})=\frac{\partial L}{\partial z}\cdot x^T$$

2-2.梯度下降法

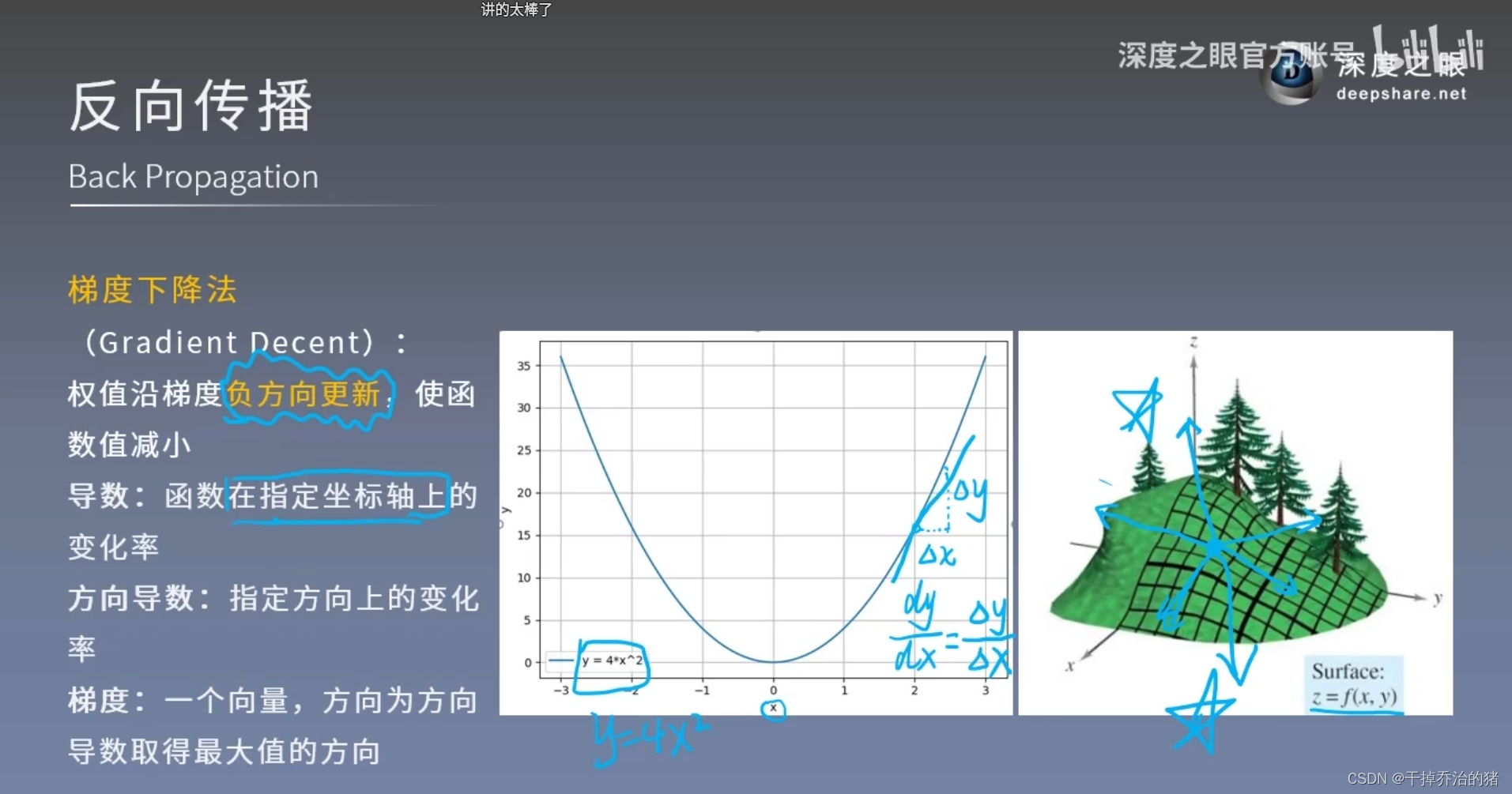
通俗解释：

梯度下降方法相当于“下山”策略：
1.“山谷的底部”相当于“函数的最小值，
2.“地面的倾斜程度”相当于“梯度”，
3.“学习率”相当于每次“移动的距离”

2-3.学习率

学习率的作用：

1.这是针对损失函数来说的。
2.学习率的作用是确保在梯度下降过程中，我们能够沿着损失函数的负梯度方向有效地更新模型的参数，从而逐步减小损失函数的值，逼近全局或局部最小值。
3.这个过程是为了找到一组参数，使得模型能够尽可能准确地预测或分类新的数据。

损失函数

1.损失函数的定义

解释：

1. 损失函数描述的是单样本的差异值
2. 代价函数描述的是总体样本的差异值
3. 目标函数强调的是整个训练过程，它由代价函数和正则项构成

1.cost描述模型与标签的差异，使模型输出与标签值更接近，减小cost的值。
2.Regularzition Term(正则项):使模型不要太复杂，减小模型的过拟合

2.MSE和CE损失函数

1. MSE:常用于回归任务中。
2. CE:常用于分类任务中。

2-1.MSE(均方误差)

公式:

$$MSE=\frac{{\sum }_{i=1}^n(y_i-y_i^p{)}^2}{n}$$

参数：
$y_i:$真实值
$y_i^p:$预测值
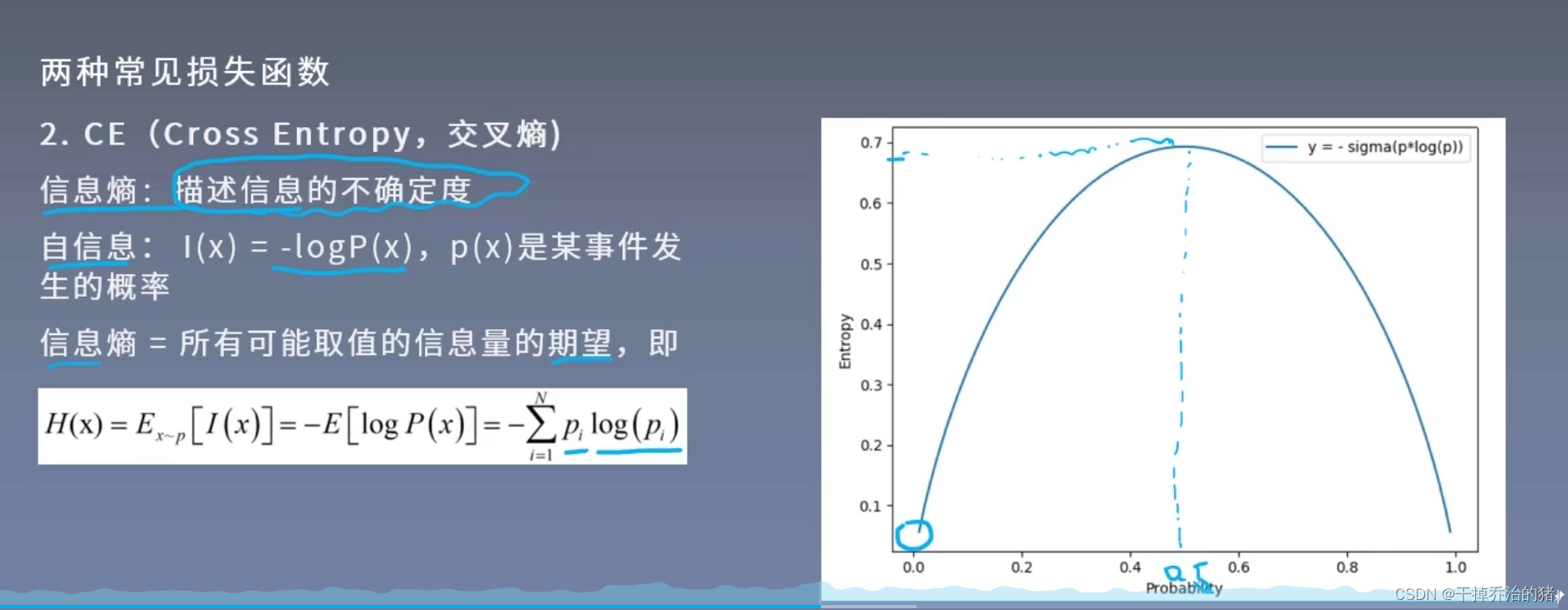
$MSE:$输出与标签值之差的平方的均值

2-2.CE（交叉熵）

公式：

$$H(p,q)=-\sum _{i=1}^{n}p(x_i)logq(x_i)$$

参数：
$p:$标签的真实值
$q:$model的输出值

信息熵：

通俗解释：
1.系统中存在很多不确定的结果
2.每种结果出现的概率大致相同
3.说明混乱程度越大，信息熵就越大

相对熵/交叉熵和信息熵之间的关系

通俗解释：

1.信息熵：衡量信息不确定的指标，比如 非常不确定的事情信息熵就很大
2.相对熵：衡量两个概率分布之间的差异
3.交叉熵：衡量模型预测的概率分布和真实标签之间的概率分布的差异，属于相对熵的一种形式！

softmax函数

softmax函数就像一个“转换器”，可以把模型的原始输出转换成一个概率分布

权值初始化

高斯分布：

1.均值：使权重围绕一个中心值（均值为0）随机分布
2.标准差：控制权重分布的离散程度

公式：

$W=N（\mu ,{\sigma }^2）$

参数：

1.$\mu :$分布的均值
2.$\sigma :$分布标准差

自适应标准差：

1.Xavier初始化方法

Xavier初始化主要适用于sigmoid和tanh激活函数。

2.kaiming初始化方法（MSRA）

Kaiming初始化主要适用于ReLu激活函数。

两种方法都是根据激活函数的特性来决定的！sigmoid和tanh激活函数中标准差既不能过大也不能过小，所以需要考虑前一层神经元和后一层神经元；而ReLu激活函数中要求标准差足够大，这样才能有利于网络的学习！

正则化方法

Regularization：

减少方差的策略，减轻过拟合的策略。

L1：

${\sum }_i^n|w_i|$

L2:

${\sum }_i^n{w}_i^2$

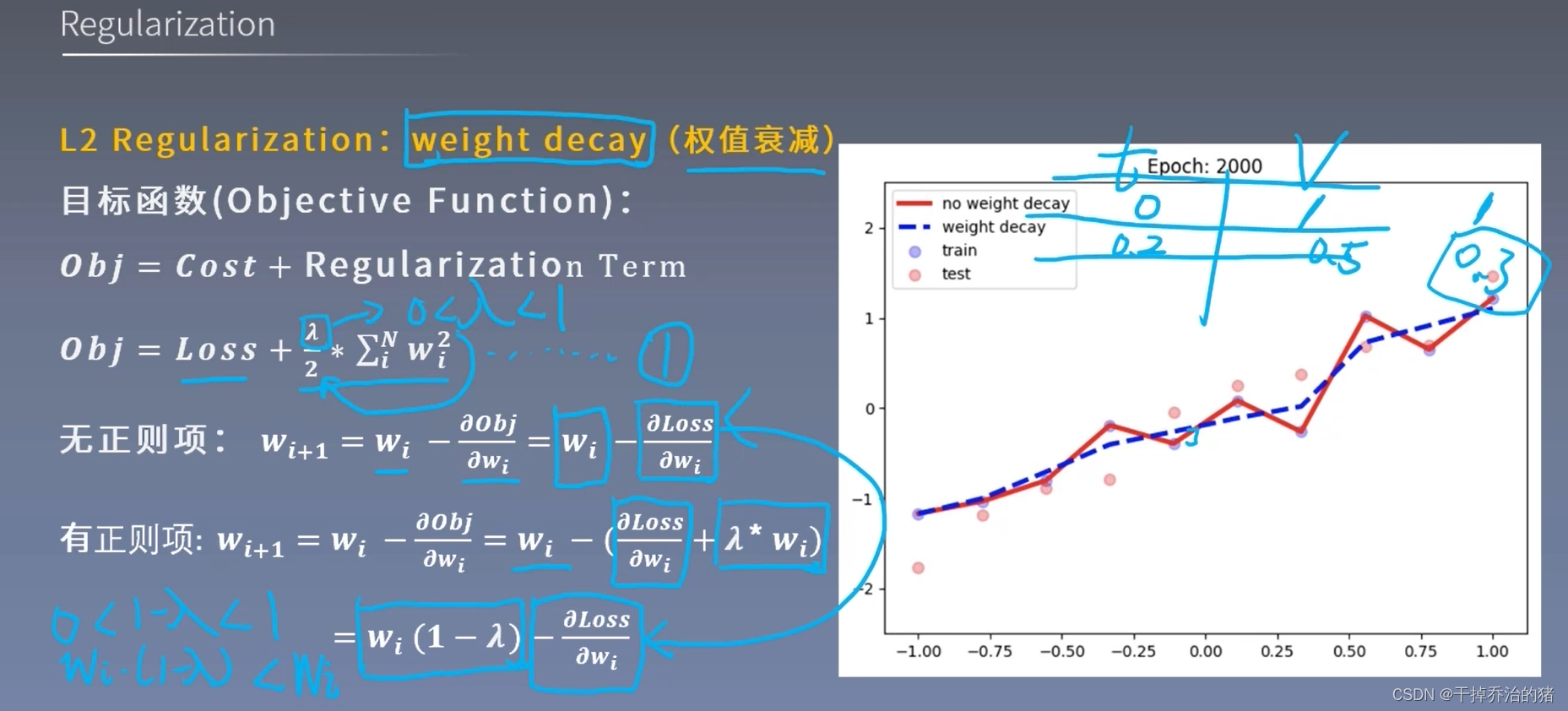
L2的权值衰减避免了模型只在训练数据上表现得好，而在新的数据集上表现差的情况。

Dropout: