AcWing dp 最长上升子序列模型学习

AcWing 895. 最长上升子序列

题意：给定一个长度为 $N$ 的数列，求数值严格单调递增的子序列的长度最长是多少。
$1\le N\le 1000$
思路：
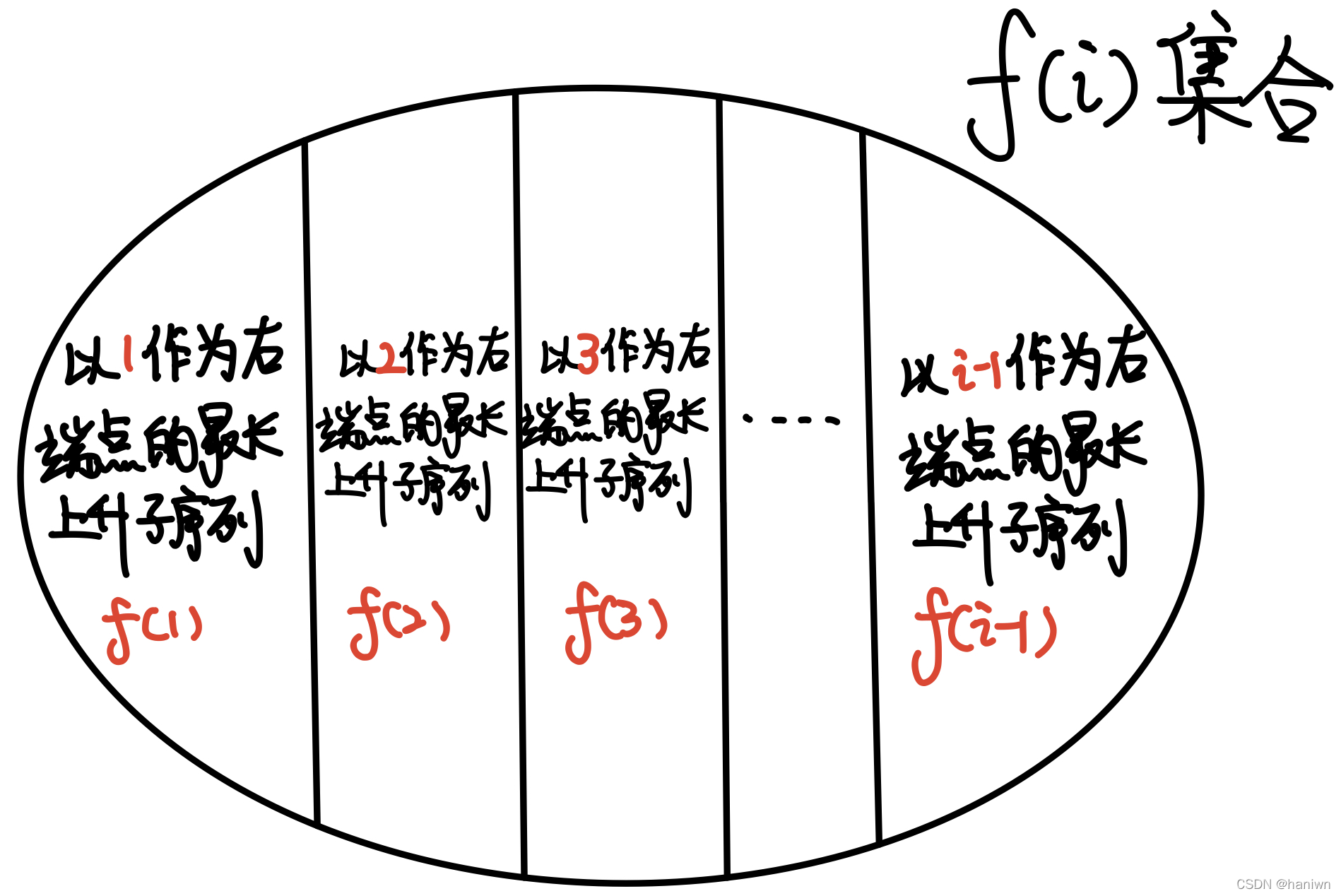
状态表达：$f[i]$ 表示从 1 开始以 $i$ 为结尾的上升子序列最大长度
状态方程：f[i] = max(f[i] , f[j] + 1)
图片来自AcWing 彩色铅笔大佬
集合划分

#include<bits/stdc++.h>
using namespace std;
const int N = 1005;
int a[N] , f[N];
int main()
{
    int n;
    cin>>n;
    for(int i = 1 ; i <= n ; i ++ ) cin>>a[i];
    for(int i = 1 ; i <= n ; i ++ )
    {
        f[i] = 1;//最少只有自己
        for(int j = 1 ; j < i ; j ++ )  
            if(a[i] > a[j]) f[i] = max(f[i] , f[j] + 1);
    }
    int res = 0;
    for(int i = 1; i <= n ; i ++ )  res = max(res , f[i]);
    cout<<res;
    return 0;
}

数据加强贪心做法

$1\le N\le 100000$
时间复杂度：$O(nlogn)$
思路：对于每个元素前面可能有若干个小于它的值，那么它可以有多种连接方法，显然接在一个数值较小的数后面是更良好的，那么对此我们可以维护若干长度不同的上升序列，使每一个结尾是最小的，也就是找一个结尾最小的长度为k的上升序列，那么这些个长度不同的上升序列的结尾元素显然是满足单调递增，因为如果长度为5的结尾元素小于长度为4的结尾元素，则显然长度为4的结尾元素不满足最小，由此可以开一个数组记录长度为 $i$ 的上升序列结尾元素，这个数组满足单调性，就可以二分实现。

#include<bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
int a[N] , q[N];
int n;
int main()
{
    cin>>n;
    for(int i = 1 ; i <= n ; i ++ ) cin>>a[i];
    int len = 0;
    for(int i = 1 ; i <= n ; i ++ )
    {
        int l = 0 , r = len;
        while(l < r)
        {
            int mid = l + r + 1>> 1;
            if(q[mid] < a[i])   l = mid;
            else r = mid - 1;
        }
        len = max(r+1,len);
        q[r + 1] = a[i];
    }
    cout<<len;
    return 0;
}

栈做法

#include<bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
int a[N],n;
int main()
{
    cin>>n;
    for(int i = 0 ; i < n ; i ++ )  cin>>a[i];
    vector<int> st;//模拟栈
    st.push_back(a[0]);
    for(int i = 1 ; i < n ; i ++ )
    {
        if(st.back() < a[i]) st.push_back(a[i]);
        else *lower_bound(st.begin(), st.end(), a[i]) = a[i];
        //替换掉第一个大于或者等于这个数字的那个数
    }
    cout<<st.size();
    return 0;
}