拓扑排序算法

什么是拓扑排序

在图论中，拓扑排序（Topological Sorting）是一个有向无环图（DAG, Directed Acyclic Graph）的所有顶点的线性序列。且该序列必须满足下面两个条件：

1. 每个顶点出现且只出现一次。
2. 若存在一条从顶点A到顶点B的路径，那么在序列中顶点A出现在顶点B的前面。

有向无环图（DAG）才有拓扑排序，非DAG图没有拓扑排序一说。

算法思想

例如，下面这个图：

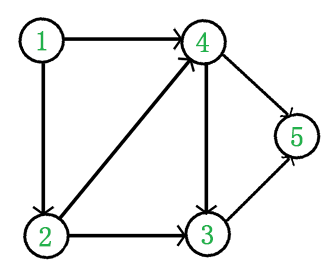
它是一个DAG图，它的一个拓扑排序为{1, 2, 4, 3, 5}

那么如何写出它的拓扑排序呢？

1. 从DAG图中选择一个没有前驱（即入度为0）的顶点并输出。
2. 从图中删除该顶点和所有以它为起点的有向边，并更新这些边关联的节点的入度。
3. 重复1和2直到当前的DAG图为空或当前图中不存在无前驱的顶点为止。后一种情况说明有向图中必然存在环。

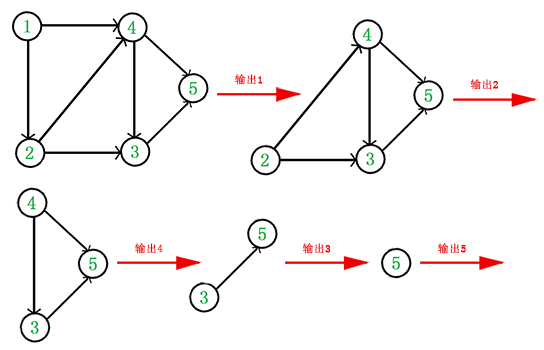
根据这种思想，我们可以得到上面那个图的一个拓扑排序为{1，2，4，3，5}，具体操作流程如下。

代码实现

输入格式：

第一行两个整数n，m分别表示节点数和边数

接下来m行，每行两个整数x，y，表示从x到y有一条边

说明：节点编号从1开始

输出格式：

一行拓扑排序，若无，输出N

样例输入：

5 7
1 4
1 2
2 4
2 3
4 5
4 3
3 5

样例输出：

1 2 4 3 5

用邻接表+队列实现如下：

#include <iostream>
#include <vector>
#include <queue>

using namespace std;

const int MAX = 10000;
queue<int> q;
vector<int> edge[MAX]; // edge[i]表示从第i个节点出去的所有节点数组
vector<int> ans;       //拓扑序列
int indegree[MAX];     //所有节点的入度

int main()
{
    int n, m; // n个节点，m条边
    cin >> n >> m;
    for (int i = 0; i < m; i++)
    {
        int from, to;
        cin >> from >> to; //从from节点到to节点有一条边
        edge[from].push_back(to);
        indegree[to]++; // to节点的入度加一
    }
    //所有入度为0的节点入队
    for (int i = 1; i <= n; i++)
    {
        if (indegree[i] == 0)
            q.push(i);
    }
    while (!q.empty())
    {
        int p = q.front(); //选一个入度为0的点，
        q.pop();           //出队列
        ans.push_back(p);
        //遍历以p为起点的所有边的终点
        for (int i = 0; i < edge[p].size(); i++)
        {
            int end = edge[p][i];
            indegree[end]--;
            if (indegree[end] == 0)
                q.push(end);
        }
    }
    if (ans.size() == n)
    {
        for (int i = 0; i < n; i++)
            cout << ans[i] << " ";
        cout << endl;
    }
    else
        cout << "N" << endl;
    return 0;
}