【蓝桥杯Java组】带你刷爆常见动态规划模型

Mymel_晗

已于 2022-04-08 16:19:58 修改

阅读量1.8k

点赞数 15

分类专栏：蓝桥杯文章标签：蓝桥杯算法 java 动态规划

于 2022-04-08 14:14:07 首次发布

本文链接：https://blog.youkuaiyun.com/m0_51338272/article/details/124022896

版权

蓝桥杯专栏收录该内容

15 篇文章

订阅专栏

header

🍋前言：

🌵🌵蓝桥杯就剩一天了，祝看到这篇文章的老铁们都有好成绩~

🌴🌴这里总结了一些动态规划的常见模型，最后一天拿来复习一波，万一中了呢🤣

🍍1.最大子段和

最大子段和或者叫最大子数组和。
f(i)代表以第 i个数结尾的「连续子数组的最大和」，对数组中的任意一个位置 $n u m s [i]$ ，要么单独作为一个子段，要么和前面的子段合并,状态转移方程： $f(i)=max{(f(i−1)+nums[i],nums[i])}$ 。

🚀题目链接：LeetCode53.最大子数组和

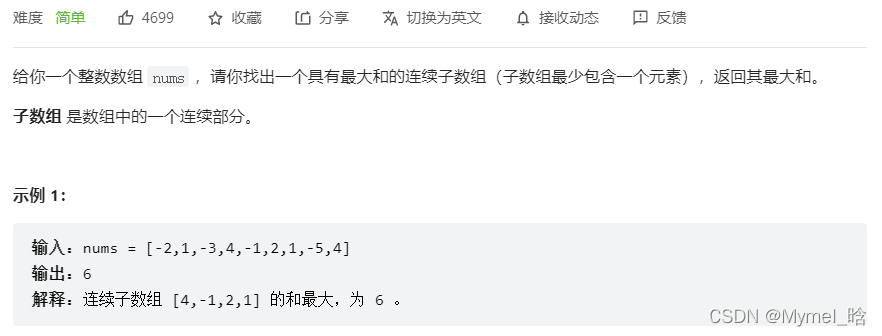
🍦参考代码（Java）：

class Solution {
    public int maxSubArray(int[] nums) {
        int len = nums.length;
        int[] dp = new int[len];
        dp[0] = nums[0];
        int max = dp[0];
        for (int i = 1; i < len; i++) {
            dp[i] = nums[i] + Math.max(dp[i -1], 0);
            max = Math.max(max, dp[i]);
        }
        return max;
    }   
}

🍓2.最长递增子序列

🚀题目链接：LeetCode300.最长递增子序列

最长递增子序列Longest Increasing Subsequence，即LIS。
$d p [i]$ 表示选择 $n u m s [i]$ ，并且以 $n u m s [i]$ 结尾的最长上升子序列的长度。
需要双层循环for i = 1 ~ nums.length，for j = 0 ~ i，如果 $n u m s [i] > n u m s [j]$ ，说明构成了一个递增对，状态转移： $dp[i] = max{(dp[i], dp[j] + 1)}$ ，最后返回 $d p$ 数组中的最大值即为答案。

🍦参考代码（Java）：

class Solution {
    public int lengthOfLIS(int[] nums) {
        int n = nums.length;
        int[] dp = new int[n];
        Arrays.fill(dp,1);
        //base case : dp[0] = 1;
        for (int i = 1;i < n; i++){
            for (int j = 0; j < i; j++){
                if (nums[j] < nums[i])
                    dp[i] = Math.max(dp[j]+1,dp[i]);
            }
        }
        int ans = 0;
        for (int i = 0; i < n;i++)
            ans = Math.max(ans,dp[i]);
        return ans;
    }
}

🍊3.最长公共子序列

🚀题目链接：LeetCode1143.最长公共子序列

最长公共子序列 Longest Common Subsequence，即LCS。
题目涉及两个字符串，使用二维dp[][]，dp[i][j]表示第一个字符串的0~i前缀子串与第二个字符串的0~j前缀子串的最长公共子序列。
若第一个字符串的i位置与第二个字符串的j位置的两个字符相等，则 $d p [i] [j] = d p [i - 1] [j - 1] + 1$ ，若两个位置的字符不等则 $d p [i] [j]$ 取 $d p [i - 1] [j]$ 与 $d p [i] [j - 1]$ 的最大值。
状态转移方程：

🍦参考代码（Java）：

class Solution {
    public int longestCommonSubsequence(String text1, String text2) {
        int len1 = text1.length();
        int len2 = text2.length();
        int[][] dp = new int[len1+1][len2+1];
        for (int i = 1; i <= len1; i++) {
            for (int j = 1; j <= len2; j++) {
                if (text1.charAt(i-1) == text2.charAt(j-1))
                    dp[i][j] = dp[i-1][j-1] + 1;
                else
                    dp[i][j] = Math.max(dp[i-1][j],dp[i][j-1]);
            }
        }
        return dp[len1][len2];
    }
}

🍈4.编辑距离

🚀题目链接：LeetCode72.编辑距离

题目涉及两个字符串，使用二维dp[][]。
$d p [i] [j]$ 表示word1的前i个字母转换成word2的前j个字母所使用的最少操作。
若 $w o r d [i] = w o r d [j]$ ，状态转移： $d p [i] [j] = d p [i - 1] [j - 1]$ 。
若 $\not= word[j]$ ，说明当前位置需要一次修改，再加上之前需要修改的次数，则状态转移： $d p [i] [j] = m i n (d p [i] [j - 1], d p [i - 1] [j], d p [i - 1] [j - 1]) + 1$

🍦参考代码（Java）：

class Solution {
    public int minDistance(String word1, String word2) {
        int len1 = word1.length();
        int len2 = word2.length();
        int[][] dp = new int[len1+1][len2+1];
        for (int i = 1; i <= len1; i++)
            dp[i][0] = i;
        for (int i = 1; i <= len2; i++)
            dp[0][i] = i;
        for (int i = 1; i <= len1; i++) {
            for (int j = 1; j <= len2; j++) {
                if (word1.charAt(i-1) == word2.charAt(j-1))
                    dp[i][j] = dp[i-1][j-1];
                else
                    dp[i][j] = Math.min(dp[i-1][j-1], Math.min(dp[i-1][j],dp[i][j-1]))+1;
            }
        }
        return dp[len1][len2];
    }
}

🍑5. 01背包问题

🚀题目链接：https://oj.czos.cn/p/1282

题目描述

有一个背包能装的重量maxw(正整数，0≤maxw≤20000)，同时有n件物品(0≤n≤100)，每件物品有一个重量wi(正整数)和一个价值pi(正整数)。要求从这n件物品中任取若干件装入背包内，使背包的物品价值最大。

输入

第1行：背包最大载重maxw，物品总数n
第2行到第n+1行：每个物品的重量和价值

输出

一个数字即背包内物品最大价值

样例：

输入
10 3
4 5
3 4
6 9
输出
14

二维dp[][]，dp[i][j]对于前i个物品，放在背包，重量不超过j的前提下，所获得的最大价值为dp[i][j]。
当第i个物品的重量大于j，说明放不进去，状态转移： $d p [i] [j] = d p [i - 1] [j]$ 。
当第i个物品的重量小于j，说明可以装包，设第i个物品的重量为 $c_i$ ，重量 $w_i$ ，状态转移： $dp[i][j] = max(dp[i - 1][j],dp[i - 1][j - c_i] + w_i）$ 。

🍦参考代码（Java）：

import java.util.Scanner;

public class Main {

    public static int n;
    public static int maxw;
    public static int[] w = new int[105];
    public static int[] p = new int[105];

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        maxw = sc.nextInt();
        n = sc.nextInt();
        for (int i = 1; i <= n; i++) {
            w[i] = sc.nextInt();
            p[i] = sc.nextInt();
        }
        int[][] dp = new int[n + 1][maxw + 1];
        for (int i = 1; i <= n; i++) {
            for (int j = 0; j <= maxw; j++) {
                if (w[i] > j) {
                    dp[i][j] = dp[i - 1][j];
                } else {
                    dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - w[i]] + p[i]);
                }
            }
        }
        System.out.println(dp[n][maxw]);
        sc.close();
    }
}

🍸01背包优化（状态压缩）：

由状态转移方程不难发现，对于dp[i][...]只和它的上一行dp[i - 1][...]有关系，可以在空间上做一下优化。
可以使用一个一维数组滚动记录dp[i][...]的上一行数据。
在一维数组上要从后向前推导，不然dp[i][j]的值会被覆盖掉，向后推会出错。
状态转移返程为： $d p [j] = m a x (d p [j], p [i] + d p [j - w [i]])$

🍦参考代码（Java）：

import java.util.Scanner;

public class Main {

    public static int n;
    public static int maxw;
    public static int[] w = new int[105];
    public static int[] p = new int[105];

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        maxw = sc.nextInt();
        n = sc.nextInt();
        for (int i = 1; i <= n; i++) {
            w[i] = sc.nextInt();
            p[i] = sc.nextInt();
        }
        int[] dp = new int[maxw + 1];
        for (int i = 1; i <= n; i++) {
            for (int j = maxw; j >= w[i]; j--) {
                dp[j] = Math.max(dp[j], dp[j - w[i]] + p[i]);
            }
        }
        System.out.println(dp[maxw]);
        sc.close();
    }
}

🍐6.多重背包问题

🚀题目链接：https://oj.czos.cn/p/1888

题目描述

有 $N$ 种物品和一个容量是 $V$ 的背包。
第i种物品最多有 $S_i$ 件，每件体积是 $V_i$ ，价值是 $W_i$ 。
求解将哪些物品装入背包，可使物品体积总和不超过背包容量，且价值总和最大。
输出最大价值。

输入

第一行两个整数， $N$ ， $V$ ，用空格隔开，分别表示物品种数和背包容积。

接下来有 $N$ 行，每行三个整数 $v_i,w_i,s_i$ ，用空格隔开，分别表示第 i 种物品的体积、价值和数量。

$0 < N, V \leq 100$
$0<v_i,w_i,s_i≤100$

输出

输出一个整数，代表最大价值。

样例

输入
4 10
3 2 2
4 3 2
2 2 1
5 3 4
输出
8

将多重背包转换为01背包。
将 $S_i$ 件物品都存起来，转换为有 $S_i$ 个物品，每个物品有一件。
这里并不需要改变dp[][]数组的长度从而真的将物品拆分成一件，只需要在01背包的基础上加一层循环即可。

🍦参考代码（Java）：

import java.util.Scanner;

public class Main {

    public static int n;
    public static int v;
    public static int[] v_i = new int[105];
    public static int[] w_i = new int[105];
    public static int[] s_i = new int[105];
    
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        n = sc.nextInt();
        v = sc.nextInt();
        for (int i = 1; i <= n; i++) {
            v_i[i] = sc.nextInt();
            w_i[i] = sc.nextInt();
            s_i[i] = sc.nextInt();
        }
        int[] dp = new int[v + 1];
        for (int i = 1; i <= n; i++) {
            for (int k = 1; k <= s_i[i]; k++) {
                for (int j = v; j >= v_i[i]; j--) {
                    dp[j] = Math.max(dp[j], dp[j - v_i[i]] + w_i[i]);
                }
            }
        }
        System.out.println(dp[v]);
    }
}

🍏7.完全背包问题

🚀题目链接：https://oj.czos.cn/p/1780

题目描述

仙岛上种了无数的不同种类的灵芝，小芳跟着爷爷来到仙岛采摘灵芝。由于他们带的食物和饮用水有限，必须在时间t内完成采摘。
假设岛上有m种不同种类的灵芝，每种灵芝都有无限多个，已知每种灵芝采摘需要的时间，以及这种灵芝的价值；
请你编程帮助小芳计算，在有限的时间t内，能够采摘到的灵芝的最大价值是多少？

输入

输入第一行有两个整数T（1 <= T <= 100000）和M（1 <= M <= 2000），用一个空格隔开，T代表总共能够用来采灵芝的时间，M代表岛上灵芝的种类数。接下来的M行每行包括两个在1到10000之间（包括1和10000）的整数，分别表示采摘某种灵芝的时间和这种灵芝的价值。

输出

输出一行，这一行只包含一个整数，表示在规定的时间内，可以采到的灵芝的最大总价值。

样例

输入
70 3
71 100
69 1
1 2
输出
140

题目完全可以看成是背包问题，时间相当于背包问题的体积，不过与01背包的区别在于物品有无限个，这种背包叫做完全背包。

⭐回顾一下01背包：

设物品重量 $w_i$ ，价值 $v_i$ ,01背包的状态转移方程： $f [i] [j] = m a x (f [i - 1] [j], f [i - 1] [j - w [i]] + v [i])$ 。
转换为一维滚动数组的状态转移方程： $f [j] = m a x (f [j], f [j - w [i]] + v [i])$ 。

⭐接下来试着推到完全背包的状态转移方程：

设物品件数为 $k$ ，可以想到完全背包的状态转移方程： $\times w[i]] + k \times v[i])$ ，限制条件 $1 < = k < = w / w [i]$ ，此时需要三重循环。
$k = 0$ 代表不取第i件物品，转移方程化简为： $\times w[i]] + k \times v[i])$ 。
或者把 $k = 0$ 的情况单独拿出来考虑，状态转移方程为： $\times w[i]] + k \times v[i]))$
考虑上式放第i种物品的情况，放的话至少放一件，先把这一件放进去，状态转移方程变型为：
$\times w[i]] + k \times v[i]) + v[i])$
将第 $2$ 步的式子中的j换成j - w[i]得到： $\times w[i]] + k \times v[i])$ ，结合第 $4$ 步的式子得到：
$f [i] [j] = m a x (f [i - 1] [j], f [i] [j - w [i]] + v [i])$
发现 $k$ 已经被消掉了，只需要双重循环就可以解决问题，跟01背包的状态转移方程只有一处差别，f[i - 1][j - w[i]] + v[i] 变为 f[i][j - w[i]] + v[i]。

⭐完全背包的状态转移方程已经和01背包很像了，到了这里如何做一维数组滚动优化呢？

考虑到跟01背包状态转移方程的差别，计算第i行时不需要保留第i - 1行的数据了，因此只需要从当前物品的重量 $w_i$ 正序循环至背包容量 $c$ ，状态转移方程完全不变。
$d p [j] = m a x (d p [j], d p [j - w [i]] + v [i])$

🍦参考代码（Java）：

import java.util.Scanner;

public class Main {

    public static int t;
    public static int m;
    public static int[] t_i = new int[2005];
    public static int[] v_i = new int[2005];
    
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        t = sc.nextInt();
        m = sc.nextInt();
        for (int i = 1; i <= m; i++) {
            t_i[i] = sc.nextInt();
            v_i[i] = sc.nextInt();
        }
        int[] dp = new int[t + 1];
        for (int i = 1; i <= m; i++) {
            for (int j = t_i[i]; j <= t; j++) {
                dp[j] = Math.max(dp[j], dp[j - t_i[i]] + v_i[i]);
            }
        }
        System.out.println(dp[t]);
    }
}