本文解析了包括背包问题、最大子数组和、动态规划等在内的多种经典算法问题，并提供了详细的代码实现，帮助读者深入理解算法原理。
public class Solution {
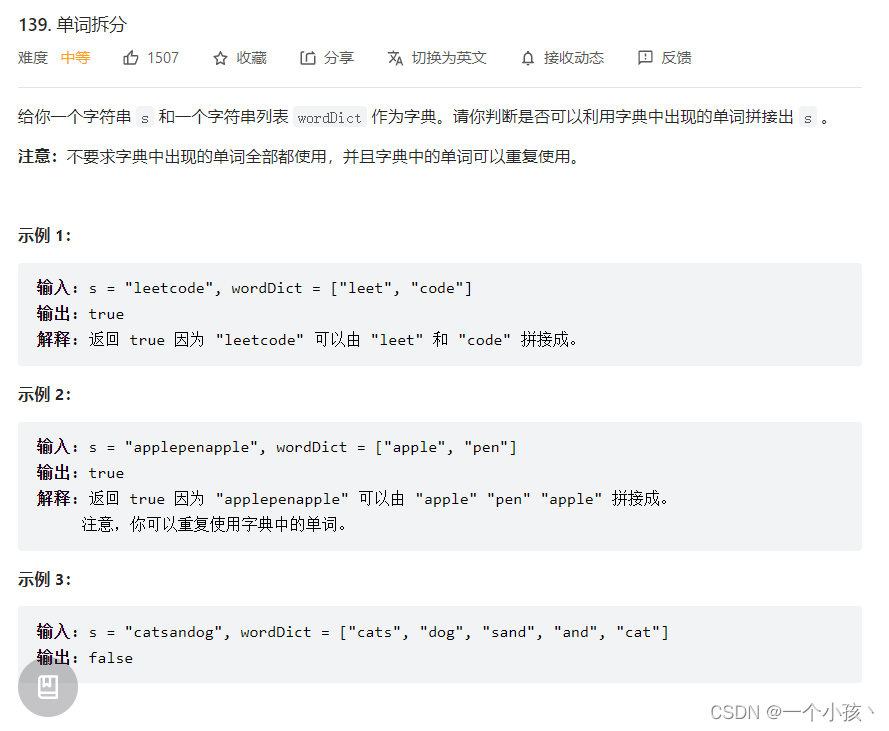
public boolean wordBreak(String s, List<String> wordDict) {
// 可以类比于背包问题
Set<String> wordDictSet = new HashSet(wordDict);
// dp[i] 表示 s 中以 i - 1 结尾的字符串是否可被 wordDict 拆分
boolean[] dp = new boolean[s.length() + 1];
//boolean类型默认的是false
dp[0] = true;
for (int i = 1; i <= s.length(); i++) {
for (int j = 0; j < i; j++) {
if (dp[j] && wordDictSet.contains(s.substring(j, i))) {
dp[i] = true;
break;
}
}
}
return dp[s.length()];
}
}
//1.13贪心算法
//明白贪心算法得意义
//3.10
//我擦，考智力啊，脑子不好使啊，直接记住吧。
//把前面的看作一个整体啊，不管是正是负，负的就从下一个开始算，＋0
// class Solution {
// public int maxSubArray(int[] nums) {
// if (nums.length == 1) return nums[0];
// int sum = 0;
// int res = Integer.MIN_VALUE;
// for (int i = 0; i < nums.length; i++) {
// sum += nums[i];
// res = Math.max(res, sum);
// //那么前面那一堆肯定是最近得那个让前面总和小于0(题目是连续部分，所以这样，理解理解)
// //而且这样还把我第一次想是负数就下一个开始得思想也包含了
// if (sum <= 0) sum = 0;
// }
// return res;
// }
// }
// 贪心贪的是哪里呢？
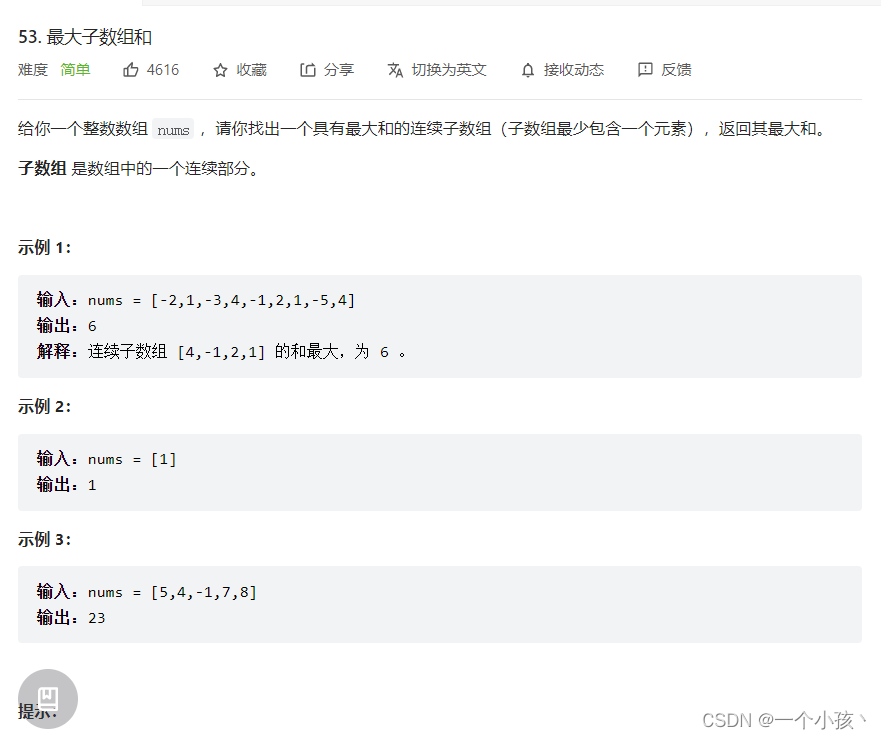
// 如果 -2 1 在一起，计算起点的时候，一定是从1开始计算，因为负数只会拉低总和，这就是贪心贪的地方！
// 局部最优：当前“连续和”为负数的时候立刻放弃，从下一个元素重新计算“连续和”，因为负数加上下一个元素 “连续和”只会越来越小。
// 全局最优：选取最大“连续和”
// 局部最优的情况下，并记录最大的“连续和”，可以推出全局最优。
// 从代码角度上来讲：遍历nums，从头开始用count累积，如果count一旦加上nums[i]变为负数，那么就应该从nums[i+1]开始从0累积count了，因为已经变为负数的count，只会拖累总和。
//3.24
//实在是太牛了，直接看题解
// public class Solution {
// public int maxSubArray(int[] nums) {
// int len = nums.length;
// // dp[i] 表示：以 nums[i] 结尾的连续子数组的最大和
// int[] dp = new int[len];
// dp[0] = nums[0];
// for (int i = 1; i < len; i++) {
// if (dp[i - 1] > 0) {
// dp[i] = dp[i - 1] + nums[i];
// } else {
// dp[i] = nums[i];
// }
// }
// // 也可以在上面遍历的同时求出 res 的最大值，这里我们为了语义清晰分开写，大家可以自行选择
// int res = dp[0];
// for (int i = 1; i < len; i++) {
// res = Math.max(res, dp[i]);
// }
// return res;
// }
// }
public class Solution {
public int maxSubArray(int[] nums) {
int[] dp = new int[nums.length];
dp[0] = nums[0];
for (int i = 1; i < nums.length; i++) {
dp[i] = Math.max(dp[i - 1] + nums[i], nums[i]);
}
int res = Integer.MIN_VALUE;
for (int x : dp) {
res = Math.max(x, res);
}
return res;
}
}
//首先想到的就是滑动窗口的最大子序列合类似，首先想到的是因为正负乘法可能会存在不同
//因为两个负就得正了
//做个记号，不是滑动窗口
//动态规划，很常用得，要时刻想着
//重点就是dp[i]代表得是以i结尾得最大子数组，而不是以i结尾得最大得乘积(也就解决了自己认为去掉第一个可能更大得疑问，因为根本不是一回事)
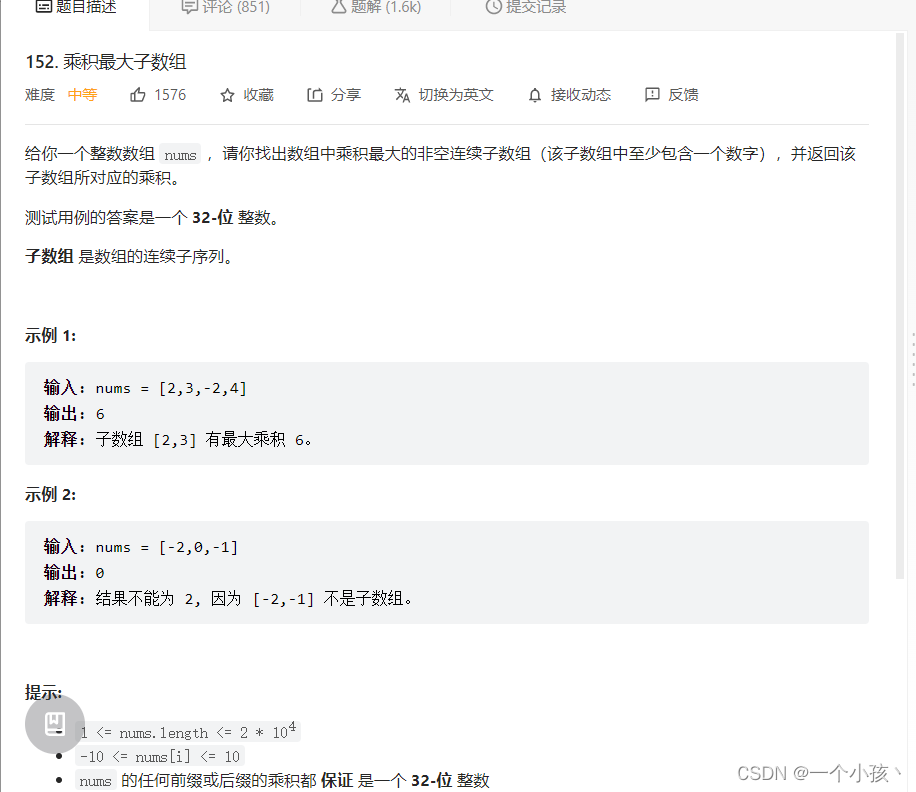
//看了weiwei得题解明白了，这个题目和最大子数组和一样得意思，动态规划
//由于存在负数，那么会导致最大的变最小的，最小的变最大的。因此还需要维护当前最小值。
class Solution {
public int maxProduct(int[] nums) {
//dp[i]同样的代表是以num[i]为结尾的最大的连续乘积子数组
int[] dpMax = new int[nums.length];
int[] dpMin = new int[nums.length];
dpMax[0] = nums[0];
dpMin[0] = nums[0];
for (int i = 1; i < nums.length; i++) {
dpMax[i] = Math.max(dpMax[i - 1] * nums[i], Math.max(nums[i], dpMin[i - 1] * nums[i]));
dpMin[i] = Math.min(dpMin[i - 1] * nums[i], Math.min(nums[i], dpMax[i - 1] * nums[i]));
}
int res = dpMax[0];
for (int x : dpMax) {
res = Math.max(res, x);
}
return res;
}
}
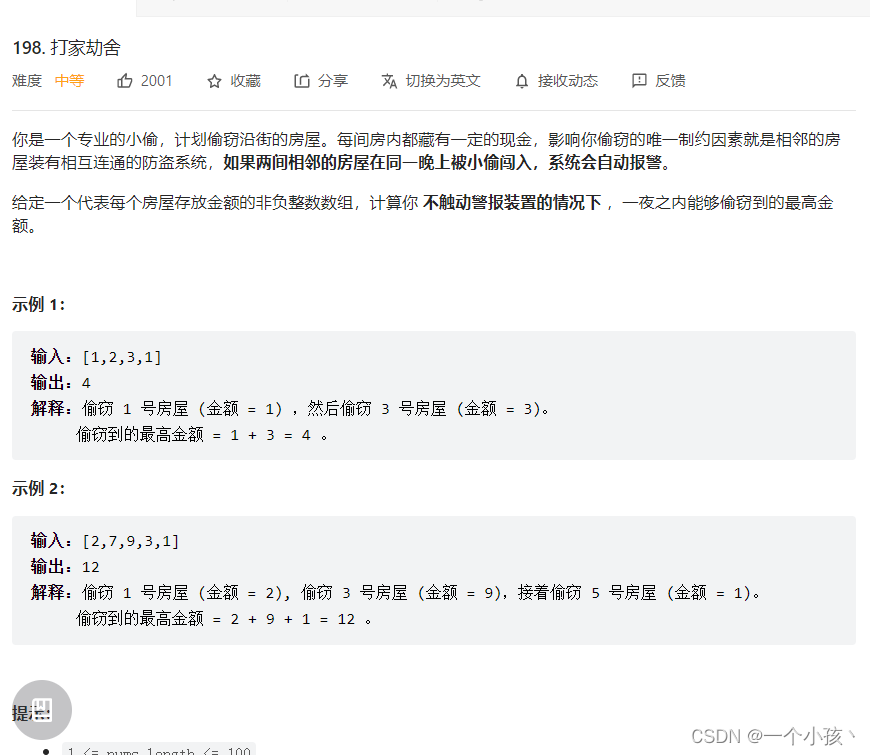
//只要求返回结果，不要求具体返回哪些，可以考虑动态规划
//其实就是从1，2到考虑多个的情况，高中题目(印象中经常这么做)
class Solution {
public int rob(int[] nums) {
if (nums.length == 1) return nums[0];
//dp[i]代表的是前i间屋子能拿到的最大总和
int[] dp = new int[nums.length];
//递推公式：
//初始化
//遍历顺序
dp[0] = nums[0];
dp[1] = Math.max(nums[0], nums[1]);
for (int i = 2; i < nums.length; i++) {
dp[i] = Math.max(dp[i - 1], dp[i -2] + nums[i]);
}
return dp[nums.length - 1];
}
}
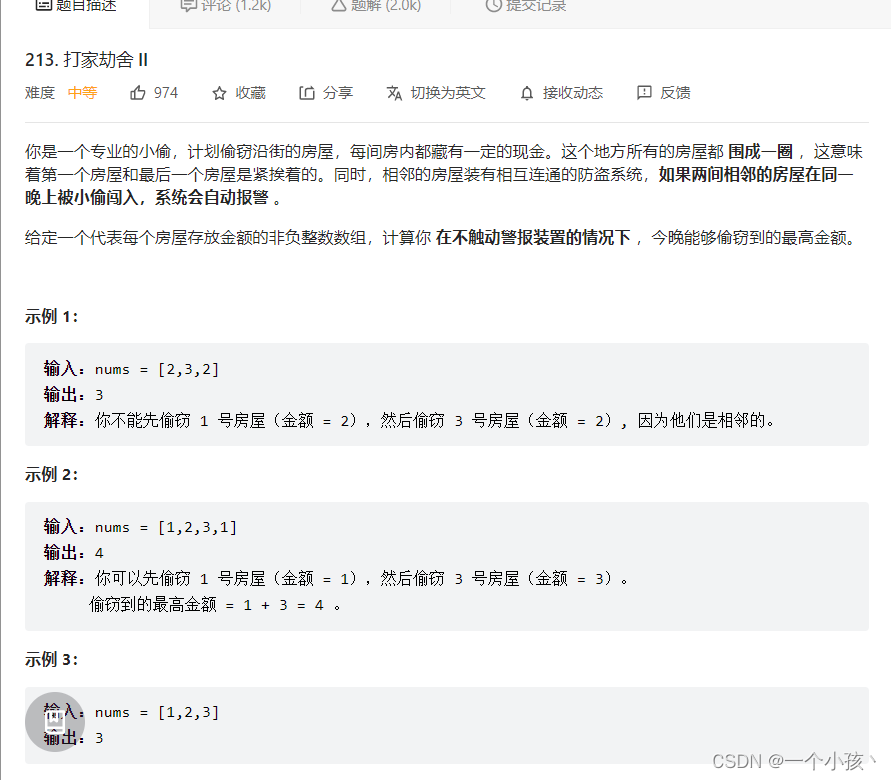
//算法题有两大核心简化复杂问题的思路：减而治之和分而治之，这题把环形分为单排就是分而治之，即把一个问题分成多个规模更小的子问题。
// class Solution {
// public int rob(int[] nums) {
// //选第一个不选最后一个
// //选最后一个不选第一个
// //这两种情况当然都包含了两者都不选啊，傻瓜
// if (nums.length == 1) return nums[0];
// return Math.max(dp(nums, 0, nums.length - 2), dp(nums, 1, nums.length - 1));
// }
// public int dp(int[] nums, int begin, int end) {
// //dp[i]表示到num[i]位置的时候能偷取的最大值
// int[] dp = new int[end + 1];
// dp[0] = nums[begin];
// dp[1] = Math.max(nums[begin], nums[begin + 1]);
// for (int i = 2; i < end + 1; i++) {
// dp[i] = Math.max(dp[i - 1], dp[i - 2] + nums[i]);
// }
// return dp[end];
// }
// }
//这是对上面方法的改进，厉害
class Solution {
public int rob(int[] nums) {
//将环分成0 - n-1 和 1 - n
//转移方程: dp[n] = Math.max(dp[n-1], dp[n-2] + nums[n])
if(nums.length == 1){
return nums[0];
}
if(nums.length == 2){
return Math.max(nums[0], nums[1]);
}
return Math.max(robber(Arrays.copyOfRange(nums,0,nums.length - 1)),
robber(Arrays.copyOfRange(nums,1,nums.length)));
}
int robber(int[] nums){
int n = nums.length;
int[] dp = new int[n+1];
dp[0] = nums[0];
dp[1] = Math.max(dp[0], nums[1]);
for(int i = 2; i < n; i++){
dp[i] = Math.max(dp[i-1], dp[i-2] + nums[i]);
}
return dp[n-1];
}
}
/**
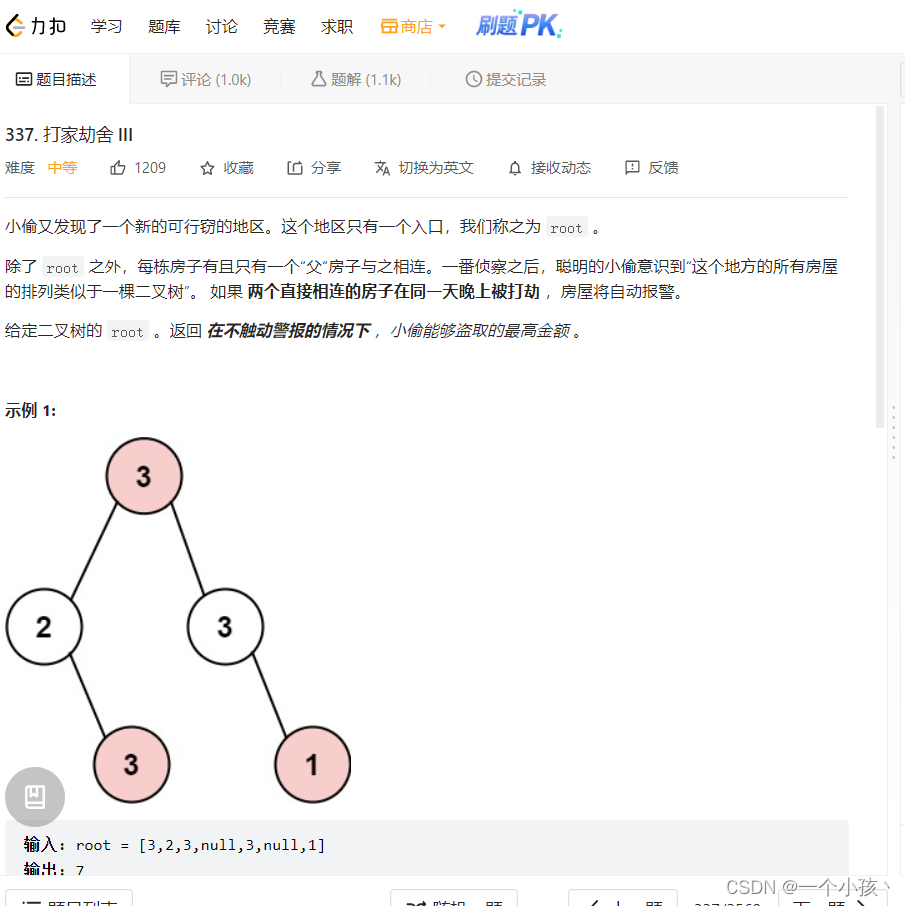
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
//每个节点可选择偷或者不偷两种状态，根据题目意思，相连节点不能一起偷
// 当前节点选择偷时，那么两个孩子节点就不能选择偷了
// 当前节点选择不偷时，两个孩子节点只需要拿最多的钱出来就行(两个孩子节点偷不偷没关系)
// 我们使用一个大小为 2 的数组来表示 int[] res = new int[2] 0 代表不偷，1 代表偷
// 任何一个节点能偷到的最大钱的状态可以定义为
// 当前节点选择不偷：当前节点能偷到的最大钱数 = 左孩子能偷到的钱 + 右孩子能偷到的钱
// 当前节点选择偷：当前节点能偷到的最大钱数 = 左孩子选择自己不偷时能得到的钱 + 右孩子选择不偷时能得到的钱 + 当前节点的钱数
class Solution {
public int rob(TreeNode root) {
int[] result = robInternal(root);
return Math.max(result[0], result[1]);
}
public int[] robInternal(TreeNode root) {
if (root == null) return new int[2];
int[] result = new int[2];
//可以利用这个题目好好理解二叉树递归，
//result数组result[0]表示不偷，result[1]表示偷，
//该节点的左右同样如此，然后计算出偷和不偷时候的最大值，还是靠智商 啊。。。说实话
int[] left = robInternal(root.left);
int[] right = robInternal(root.right);
result[0] = Math.max(left[0], left[1]) + Math.max(right[0], right[1]);
result[1] = left[0] + right[0] + root.val;
return result;
}
}
扫一扫
423
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
