算法——深度优先搜索

---

一、概念

从起点出发，搜索终点，走过的点需要标记，发现没走过的点，就随意挑一个往前走，走不了就回退，这种路径搜索的策略叫做深度优先搜索(Depth-First-Search)。

DFS算法的用途就是在图上寻找路径，比如下面这个图，思考一下如何寻找从1到8的路径。

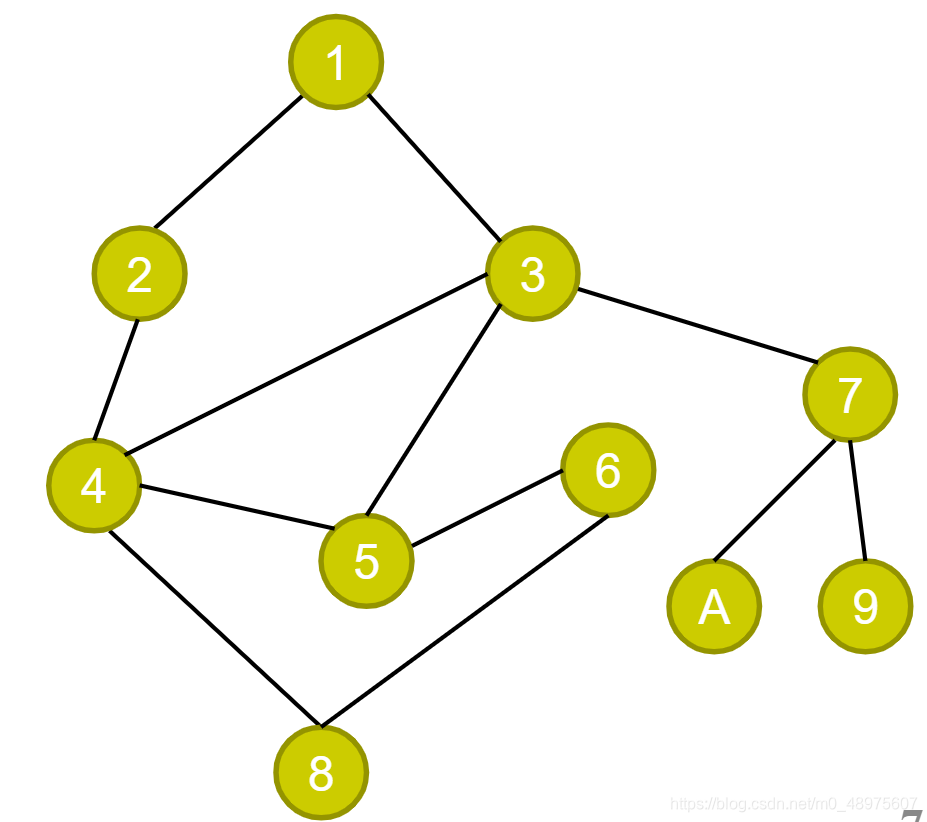
按照DFS的思路，运气好的话我们可以1->2->4->8
运气不好的话也有可能是1->3->7->9=>7->A=>7=>3->5->6->8
由此可见DFS算法的时间复杂度的可以很小也可以很大，最坏情况下需要遍历完整个图才能找到终点。

二、抽象代码

1.判断从V出发是否能走到终点

bool DFS(V)
{
	if (V是终点)
		return true;	//说明从V开始可以走到终点
	if (V是遍历过的点)
		return false;	//说明不能从V走到终点
	将V标记为遍历过的点;
	对V相邻的每个结点U {
		if (DFS(U) == true)		//如果从U开始能到达终点
			return true;		//说明从V开始也能到达终点
	}
	return false;		//执行到此说明V的所有结点以及V本身都不能到达终点
}

2.判断从V出发是否能走到终点，并记录路径

Node path[MAX_LEN];		//用来存放路径上的结点
int depth = 0;			//表示当前遍历到的深度
bool DFS(V)
{
	if (V是终点)
		path[depth] = V;
		return true;	//说明从V开始可以走到终点
	if (V是遍历过的点)
		return false;	//说明不能从V走到终点
	将V标记为遍历过的点;
	path[depth] = V;
	depth++;
	对V相邻的每个结点U {
		if (DFS(U) == true)		//如果从U开始能到达终点
			return true;		//说明从V开始也能到达终点
	}
	depth--;	
	return false;		//执行到此说明V的所有结点以及V本身都不能到达终点
}

2.遍历非连通图上的所有结点

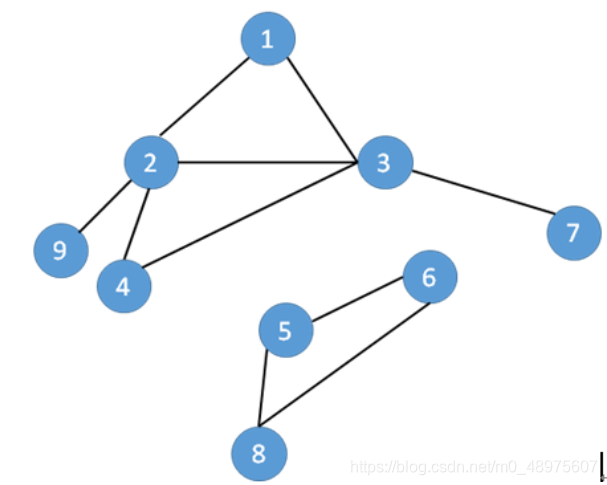
 void DFS(V)
{
	if (V是遍历过的点)
		return;
	将V标记为遍历过的点;
	对V相邻的每个结点U
		DFS(U);
}

int main()
{
	将所有点都标记为未遍历;
	while (在图中能找到新点K)
		DFS(K);
}

二、例题

1.踩方格

问题描述
有一个方格矩阵，矩阵边界在无穷远处，我们做如下假设：
a.每走一步时，只能从当前方格移动一格，走到某个相邻的方格上；
b.走过的格子立即塌陷无法再走第二次
c.只能向北、东、西三个方向走
请问：如果允许在方格矩阵上走n步（n<=20）,共有多少种不同的方案，2种走法只要有一步不一样，即被认为是不同的方案。

输入
允许在方格上行走的步数n(n≤20)。

输出
计算出的方案数量。

样例输入
2

样例输出
7

解题思路
递归
从(i,j)出发，走n步的方案数，等于以下三项之和:
从(i+1,j)出发，走n-1步的方案数。前提：(i+1,j)还没走过
从(i,j+1)出发，走n-1步的方案数。前提：(i,j+1)还没走过
从(i,j-1)出发，走n-1步的方案数。前提：(i,j-1)还没走过
我们需要设置一个标记数组visited，来记住某个方块(i,j)是否被走过。

程序代码

#include<iostream>
#include<cstring>
using namespace std;

int visited[30][50];	//用来标记是否走过

int ways(int i, int j, int n)
{
	int num = 0;		//临时存放走法数量
	if (n == 0)			//如果走到点(i,j)步数走完了
		return 1; 
	visited[i][j] = 1;	//如果没走完，将此点标记为已走过
	if (visited[i + 1][j] == 0)
		num += ways(i + 1, j, n - 1);
	if (visited[i][j + 1] == 0)
		num += ways(i, j + 1, n - 1);
	if (visited[i][j - 1] == 0)
		num += ways(i, j - 1, n - 1);
	visited[i][j] = 0;
	/*为什么这里要清0，因为前面把它置为1之后，
	中间三步就是在计算这样有多少种走法，当运行到这一步的时候，
	说明前面已经走完了，需要返回到上一层递归，就表明不走i,j要走别处。
	对应不走i,j走别处的办法，还是可以绕回i,j的，i,j其实是可以走的。 
	所以进去的时候需要置为1，出来的时候需要置为0 */
	return num;
}

int main()
{
	int n;		//要走的步数
	cin >> n;		//n<=20
	memset(visited, 0, sizeof(visited));		//将点都标记为未走过
	cout << ways(0, 25, n) << endl;		//输出共有几种走法
	return 0;
}