问题背景

复化求积公式(composite integration rule)是一类重要的求积公式。指将求积区间分为m个子区间,对每个子区间应用同一求积公式,所得到的复合数值积分公式。
在使用和证明中发现,高阶Newton-Cotes公式具有较高的代数精度,但对传播误差的控制是很差的,因此其计算效果也不理想.如果采用低阶方法,则截断误差很大,又常常达不到精度要求。
影响截断误差的一个很重要的参量求积区间的长度,如果积分区间越小,则求积公式的截断误亦越小。这就启发我们先将区间等分,然后在每一小区间上采用低节点的公式,再将其集中起来,这样得到的公式称为复化求积公式。它是提高求积公式精度的重要手段之一。
数值演算
由matlab编写程序,在n取不同值时用三种复化求积公式计算近似值,得到的结果为:
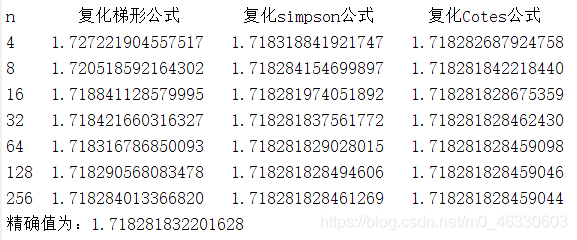
可以看到,随着n的增大,复化求积公式的精度也变得更高,且在n值相同的情况下,复化梯形公式、复化Simpson公式、复化Cotes公式的精度依次提高,这与理论情况也是吻合的。
源代码
Integration.m:








 本文探讨了复化求积公式在数值逼近中的重要性,指出高阶Newton-Cotes公式代数精度高但误差控制不佳,而低阶方法可能导致截断误差过大。通过将区间等分并应用低节点公式,可以实现复化求积公式,提高精度。通过MATLAB编程验证,随着n值增加,复化梯形、Simpson和Cotes公式的精度依次提升,符合理论预期。
本文探讨了复化求积公式在数值逼近中的重要性,指出高阶Newton-Cotes公式代数精度高但误差控制不佳,而低阶方法可能导致截断误差过大。通过将区间等分并应用低节点公式,可以实现复化求积公式,提高精度。通过MATLAB编程验证,随着n值增加,复化梯形、Simpson和Cotes公式的精度依次提升,符合理论预期。
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 6839
6839

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








