关于快排和归并的思考

最新推荐文章于 2024-11-27 10:48:50 发布

原创最新推荐文章于 2024-11-27 10:48:50 发布

· 682 阅读

0 ·

版权

文章标签：

#算法 #排序算法 #数据结构 #快速排序 #java

归并排序和快速排序是两种稍微复杂的排序算法，它们用的都是分治的思想，代码都通过递归来实现，过程非常相似。归并排序算法是一种在任何情况下时间复杂度都比较稳定的排序算法，这也使它存在致命的缺点，即归并排序不是原地排序算法，空间复杂度比较高，是 O(n)。正因为此它也没有快排应用广泛。快速排序算法虽然最坏情况下的时间复杂度是 O(n²)，但是平均情况下时间复杂度都是 O(nlogn)。且快速排序算法时间复杂度退化到 O(n²) 的概率非常小，我们可以通过合理地选择基准值来避免这种情况。

什么是数组的逆序度

如果用概率论方法定量分析平均时间复杂度，涉及的数学推理和计算就会很复杂。我们其实还有一种思路，通过有序度和逆序度这两个概念来进行分析。有序度是指数组中具有有序关系的元素对的个数，如下图所示：

所以对于一个倒序排列的数组，比如 6，5，4，3，2，1，有序度是 0；对于一个完全有序的数组，比如 1，2，3，4，5，6，有序度就是n\*(n-1)/2，也就是 15。我们把这种完全有序的数组的有序度叫作满有序度。逆序度的定义正好跟有序度相反(默认从小到大为有序)，所以满有序度 - 有序度 = 逆序度。

求数组的逆序度

数组的逆序度也就是数组的逆序对的个数，如果要求出来也是比较简单，直接暴力解法就可以，检查每一个数对，但是这样的时间复杂度为O(n²)。我们能否使用它更快捷的方法呢？其实是有的，那就是我们用归并排序的思路思路来解决这个问题，时间复杂度降到O(nlogn)。

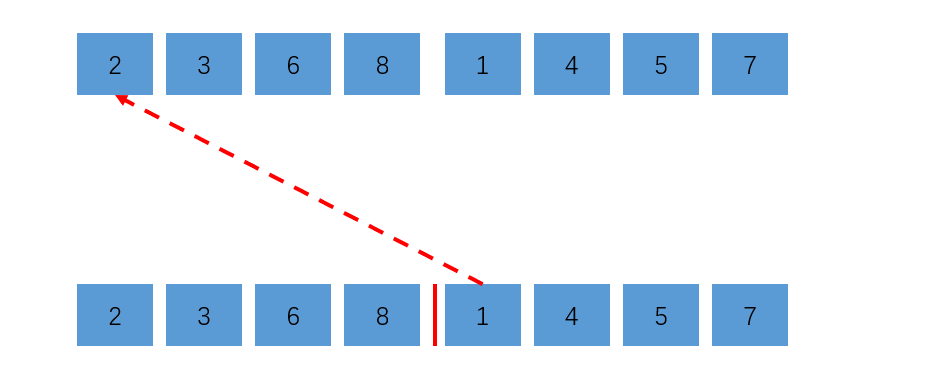
如上图所示，对于归并排序，红线两边都是已经排好序的数组，此时做归并需要把1给挪到2的位置，意思就是1这个元素比2-8这一部分元素都大，所以无序度直接+4就达到了省时间的目的。接下来的步骤如图所示：

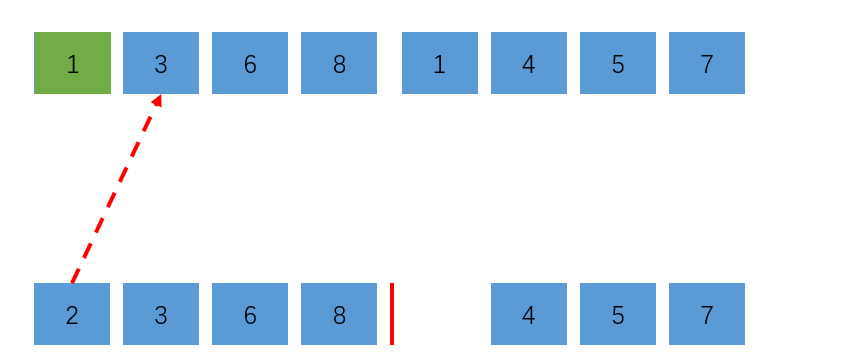
2会放在2的位置上，这也就意味着2比4以及4以后的元素都要小，那么2和4以及4以后的元素都组成了顺序对。当归并完成以后就求得了数组的逆序度：

// merge函数求出在arr[l...mid]和arr[mid+1...r]有序的基础上, arr[l...r]的逆序数对个数
private static long merge(int[] arr, int l, int mid, int r) {

    int[] aux = Arrays.copyOfRange(arr, l, r+1);

    // 初始化逆序数对个数 res = 0
    long res = 0L;

    // 初始化，i指向左半部分的起始索引位置l；j指向右半部分起始索引位置mid+1
    int i = l, j = mid+1;
    for(int k = l ; k <= r; k++ ){
        // 如果左半部分元素已经全部处理完毕
        if(i > mid){
            arr[k] = aux[j-l];
            j++;
        }
        // 如果右半部分元素已经全部处理完毕
        else if(j > r){
            arr[k] = aux[i-l];
            i++;
        }
        // 左半部分所指元素 <= 右半部分所指元素
        else if( aux[i-l] < aux[j-l]){
            arr[k] = aux[i-l];
            i++;
        }
        else{
            // 右半部分所指元素 < 左半部分所指元素
            arr[k] = aux[j-l];
            j++;
            // 此时, 因为右半部分k所指的元素小
            // 这个元素和左半部分的所有未处理的元素都构成了逆序数对
            // 左半部分此时未处理的元素个数为 mid - j + 1
            res += (long)(mid - i + 1);
        }
    }

    return res;
}

// 求arr[l..r]范围的逆序数对个数
private static long solve(int[] arr, int l, int r) {
    if (l >= r)
        return 0L;

    int mid = l + (r-l)/2;
    // 求出 arr[l...mid] 范围的逆序数
    long res1 = solve(arr, l, mid);

    // 求出 arr[mid+1...r] 范围的逆序数
    long res2 = solve(arr, mid + 1, r);

    return res1 + res2 + merge(arr, l, mid, r);
}

public static long solve(int[] arr){
    int n = arr.length;
    return solve(arr, 0, n-1);
}

求数组中第N小的元素

其实这个问题是一个明显的Top K问题，但是我们除了用堆还能用其他方法吗？其实快速排序也可以解决这个问题，我们回顾一下快速排序的过程(《快速排序及其优化》)，其实就是通过基准值每次把数组进行划分，我们只需要保留存在第N大的元素的那一部分即可，这么处理的话时间复杂度是O(n)，复杂度 = n + n/2 + n/4 + n/8 + … ，所有看成是O(n)或者O(2n)的时间复杂度，但是我们需要注意的是需要使用随机化法，来确定基准值。

public class QuickSortTopK {
    // 对arr[l...r]部分进行partition操作
    // 返回p, 使得arr[l...p-1] < arr[p] ; arr[p+1...r] > arr[p]
    // partition 过程, 和快排的partition一样
    private static int partition(int[] arr, int l, int r){
        // 随机在arr[l...r]的范围中, 选择一个数值作为标定点pivot
        swap(arr, l , (int)(Math.random()*(r-l+1))+l );

        int v = arr[l];
        int j = l; // arr[l+1...j] < v ; arr[j+1...i) > v
        for( int i = l + 1 ; i <= r ; i ++ )
            if( arr[i] < v){
                j ++;
                swap(arr, j, i);
            }

        swap(arr, l, j);

        return j;
    }

    // 求出nums[l...r]范围里第k小的数
    private static int solve(int[] nums, int l, int r, int k){
        if( l == r ) return nums[l];

        // partition之后, nums[p]的正确位置就在索引p上
        int p = partition(nums, l, r);

        // 如果 k == p, 直接返回nums[p]
        if( k == p )
            return nums[p];
        // 如果 k < p, 只需要在nums[l...p-1]中找第k小元素即可
        else if( k < p )
            return solve( nums, l, p-1, k);
        else// 如果 k > p, 则需要在nums[p+1...r]中找第k-p-1小元素
            // 注意: 由于我们传入__selection的依然是nums, 而不是nums[p+1...r],
            // 所以传入的最后一个参数依然是k, 而不是k-p-1
            return solve( nums, p+1, r, k );
    }

    // 寻找nums数组中第k小的元素
    // 注意: 在我们的算法中, k是从0开始索引的, 即最小的元素是第0小元素, 以此类推
    // 如果希望我们的算法中k的语意是从1开始的, 只需要在整个逻辑开始进行k--即可, 可以参考solve2
    public static int solve(int[] nums, int k) {
        assert nums != null && k >= 0 && k < nums.length;
        return solve(nums, 0, nums.length - 1, k);
    }

    private static void swap(int[] arr, int i, int j) {
        int t = arr[i];
        arr[i] = arr[j];
        arr[j] = t;
    }

    // 测试 Selection
    public static void main(String[] args) {
        // 生成一个大小为n, 包含0...n-1这n个元素的随机数组arr
        int N = 10;
        int[] arr = SortTestHelper.generate(N, 0, N);
        for(int i: arr) System.out.print(i + " ");
        System.out.println();
        int solve = solve(arr, 3);
        System.out.println(solve);
    }
}