信息增益比 vs 信息增益

表一 满足什么情况才去玩高尔夫 

Day	Temperatrue	Outlook	Humidity	Windy	PlayGolf?
07-05	hot	sunny	high	false	no
07-06	hot	sunny	high	true	no
07-07	hot	overcast	high	false	yes
07-09	cool	rain	normal	false	yes
07-10	cool	overcast	normal	true	yes
07-12	mild	sunny	high	false	no
07-14	cool	sunny	normal	false	yes
07-15	mild	rain	normal	false	yes
07-20	mild	sunny	normal	true	yes
07-21	mild	overcast	high	true	yes
07-22	hot	overcast	normal	false	yes
07-23	mild	sunny	high	true	no
07-26	cool	sunny	normal	true	no
07-30	mild	sunny	high	false	yes

 

---

决策树是机器学习中的经典算法，分别由三个经典算法实现：ID3，C4.5，CART，这三个算法最明显的区别就是对于特征选择的策略不同，不过目的只有一个：使当前数据集的混乱程度降低。具体来说，ID3ID3使用的信息增益，C4.5使用的信息增益比，CART使用的Gini指数（基尼指数）

对于ID3和C4.5的信息增益和信息增益比有什么区别呢，为什么放着信息增益不用，又要计算一个gainratio呢？这就是下面的内容要讨论的。

讨论之前先来几个公式压压惊。

在信息论与概率统计中，熵（entropy）是表示随机变量不确定性的度量[2]。设X的概率分布为

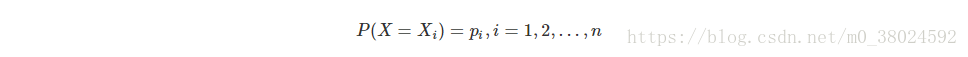
则随机变量XX 的熵定义为

 

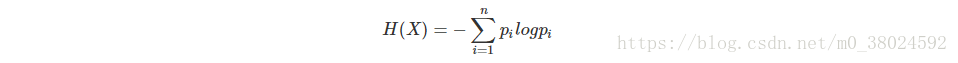
其实公式看起来挺吓人的，但是计算的时候很简单。拿表一作为计算的例子，假设

 

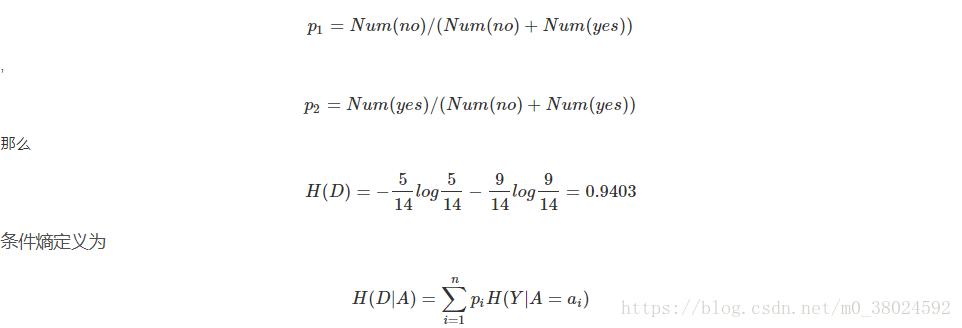
本来ID3算法计算信息增益好好的，但是C4.5一定要计算信息增益比(gainratio)这是为什么呢？ 
还是以表一为例，假如我们想用Day来做为特征(当然实际上一般人也不会傻到用Day用做特征)，显然，每一天都可以将样本分开，也就是形成了一颗叶子数量为14，深度只有两层的树。这种样本分隔的结果就是计算出来的H(D|Day)=0,那么g(D,Day)=0.9403，这特征可真是够“好”的！不过显然这种特征对于样本的分隔没有任何意义。类似的情况还有人们的身份证号、信用卡号、学号等等特征。 
那么导致这样的偏差的原因是什么呢？从上面的例子应该能够感受出来，原因就是该特征可以选取的值过多。解决办法自然就想到了如何能够对树分支过多的情况进行惩罚，这样就引入了下面的公式，属性A的内部信息（Intrinsic Information of an Attribute）：

 

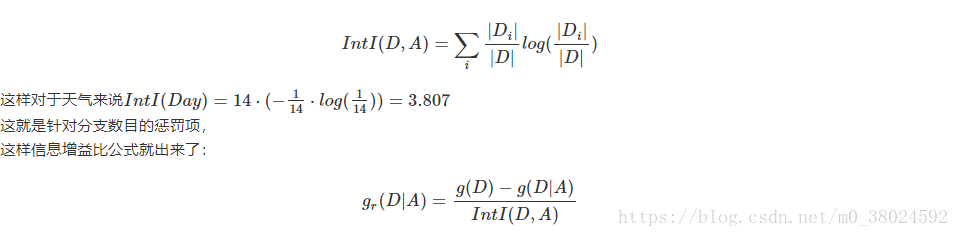
总结上面的公式，计算得到下表：

OutLook	Temperatrue
Gain:0.940-0.693 = 0.247	Gain:0.940-0.911 = 0.029
Gain ratio: 0.245/1.577 = 0.157	Gain ratio:0.029/1.557 = 0.019

Humidity	Windy
Gain:0.940-0.788 = 0.152	Gain:0.940-0.911 = 0.029
Gain ratio: 0.152/1.000 = 0.152	Gain ratio:0.048/0.985 = 0.049

Day
Gain ratio:0.940/3.807 = 0.246

然而。。。最终还是DayDay的特征优势最大。。。Orz 
不过虽然这样，信息增益率还是要比信息增益可靠的多的！另外也可以看出，对特征的筛选也是非常重要的步骤，可以减少信息增益率失效的几率。

[1] http://www.ke.tu-darmstadt.de/lehre/archiv/ws0809/mldm/dt.pdf 
[2] 李航. 统计学习方法.

转载自：https://blog.youkuaiyun.com/olenet/article/details/46433297