[LeetCode]C语言-Next Permutation-程序优化之路

Implement next permutation, which rearranges numbers into the lexicographically next greater permutation of numbers.

If such arrangement is not possible, it must rearrange it as the lowest possible order (ie, sorted in ascending order).

The replacement must be in-place and use only constant extra memory.

Here are some examples. Inputs are in the left-hand column and its corresponding outputs are in the right-hand column.

1,2,3 → 1,3,2
3,2,1 → 1,2,3

1,1,5 → 1,5,1

首先看到这个题目，对于我这个英语废物来说多么痛苦，我硬着头皮再上网搜索才最终明白了。这道题就是求这个组合的下一个排列，下一个排列比上一个大。简单举个例子，{1，2，3}的排列依次为

1,2,3 →  1,3,2 →  2,1,3 → 2,3,1 → 3,1,2 → 3,2,1

我们从后往前看可以以发现，如果后面是一个递增序列如{3，1，2}，只需将后面两个元素互换即可得{3，2，1}。如果后面为一个递减序列如{2，3，1}，那就比较麻烦，因为后面两个数已经最大，只能换递减序列的前一位”2“，所以从后面的递减序列中找到最小的比“2”大的数“3”，将这两个互换位置，得到{3，2，1}，这样就结束了吗？当然没有，还要将最后的序列调为递增得到结果{3，1，2}。就是这样，我们现在看一个比较复杂的例子：{5，4，7，5，3，2}来验证我们的规律。

1.首先看它的结尾是什么序列，{7，5，3，2}递减序列。

2.将其递减序列前一位“4”与递减序列中的最小的比“4”大的数“5”互换位置得{5，5，7，4，3，2}。

3.将改变后的递减序列调为递增序列的{5，5，2，3，4，7}。

我们使用这个规律实现我们的代码：

8ms

void swap(int* a, int* b) {
    int tmp = 0;
    tmp = *a;
    *a = *b;
    *b = tmp;
}
void nextPermutation(int* nums, int numsSize) {
    int i = numsSize - 1;
    int icount = 0;
    int dcount = 0;
    int head = 0;

    //判断后面为递减序列还是递增序列
    for(i = numsSize - 1; i > 0; i--) {
        if(nums[i] > nums[i-1]) {
            if(dcount > 0) {
                head = i-1;
                break;
            }
            icount++;
        }
        else {
            if(icount > 0) {
                //找到递减序列前一个元素
                head = i-1;
                break;
            }
            dcount++;
        }
    }
    //递增序列交换最后两位
    if(icount > 0) {
        swap(&nums[numsSize - 1], &nums[numsSize - 2]);
    }
    //递减序列
    if(dcount > 0) {
        //整个排列为递减
        if(dcount == numsSize - 1) {
            i = 0;
            while(i < numsSize/2){
                 swap(&nums[i], &nums[numsSize - i - 1]);
				 i++;
            }
        }
        //最后为递减序列
        else {
            //找到递减序列中最小的比前一个元素大的元素
            while(nums[head] < nums[i] && i < numsSize) {
                i++;
            }
            //交换这两个元素
            swap(&nums[i - 1], &nums[head]);
			i = head + 1;
            //将改变后的递减序列变为递增序列
			while(i < (numsSize + head - i)){
                 swap(&nums[i], &nums[numsSize + head - i]);
				 i++;
            }
        }
    }
}

运行结果：

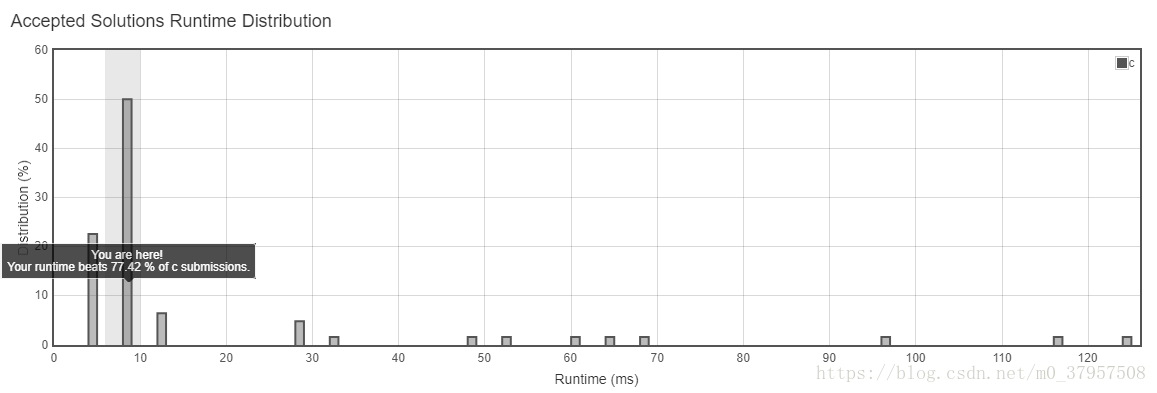
虽然已经成功了，但是我的强迫症又犯了，每到100%就看着不舒服，于是我试着再优化一下程序，然后发现递增序列判定冗余了，因为递增我们是互换最后两位位置，我们判定递增只需判定一次就可以了，无需判定多次，最后得到我们的最后的版本。

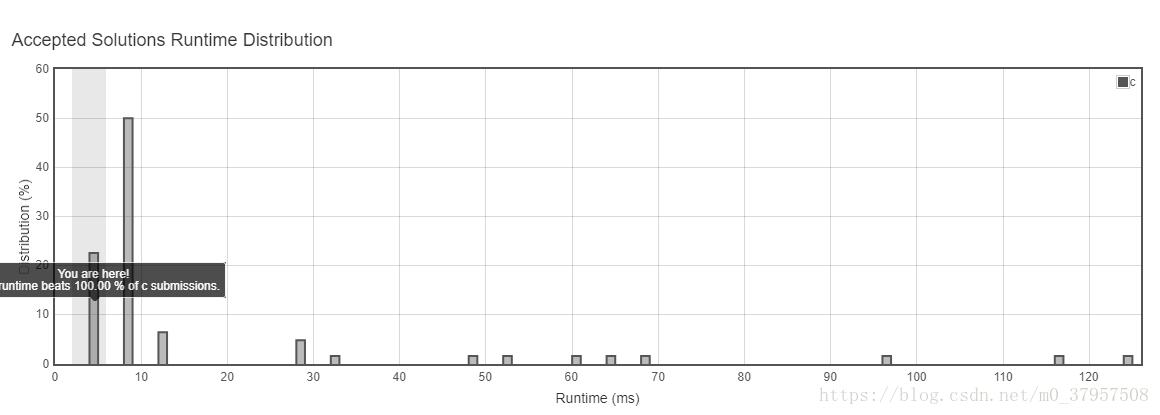
4ms

void swap(int* a, int* b) {
    int tmp = 0;
    tmp = *a;
    *a = *b;
    *b = tmp;
}
void nextPermutation(int* nums, int numsSize) {
    int i = numsSize - 1;
    int dcount = 0;
    int head = 0;
    int end = 0;
	int j = 0;
    if(numsSize < 2) {
        return 0;
    }
    for(; i > 0; i--) {
        if(nums[i] <= nums[i-1]) {
            dcount++;
        }
        else {
            head = i - 1;
            break;
        }
    }
    if(dcount == 0) {
        swap(&nums[numsSize - 1], &nums[numsSize - 2]);
    }
    if(dcount > 0) {
        if(dcount == numsSize - 1) {
            i = 0;
            while(i < numsSize/2){
                 swap(&nums[i], &nums[numsSize - i - 1]);
				 i++;
            }
        }
        else {
            while(nums[head] < nums[i] && i < numsSize) {
                i++;
            }
            swap(&nums[i - 1], &nums[head]);
			i = head + 1;
			while(i < (numsSize + head - i)){
                 swap(&nums[i], &nums[numsSize + head - i]);
				 i++;
            }
        }
    }
}

运行结果：