比赛通道
A题:VIPKID大数据“黑科技”:为小朋友智能匹配最佳外教
题解
1、保证每个括号都能合法匹配。
2、满足反回文串的性质。(反回文串性质,字符串对称位置符号不相同)
不合法匹配样例:
)(
((()
利用栈的性质,轻松解题。
独立贴上板子,减少无效代码量
#include<iostream>
#include<queue>
#include<cstring>
#include<string>
#include<sstream>
#include<map>
#include<vector>
#include<cstdio>
#include<set>
#include<cmath>
#include<algorithm>
#include<cstdlib>
#include<stack>
#include<ctime>
using namespace std;
#define rep(i,aa,bb) for(register int i=aa;i<=bb;i++)
#define rrep(i,aa,bb) for(register int i=aa;i>=bb;i--)
#define mset(var,val) memset(var,val,sizeof(var))
#define LL long long
#define eps 0.000001
#define inf 0x7f7f7f7f
#define llinf 1e18
#define exp 0.000001
#define pai 3.141592654
#define random(x) rand()%(x)
#define lowbit(x) x&(-x)
inline int read()
{
int x=0,y=1;char a=getchar();while ( a>'9' || a<'0'){if ( a=='-')y=-1;a=getchar();}
while ( a>='0' && a<='9' ){ x=(x<<3)+(x<<1)+a-'0'; a=getchar();}return x*y;
}
AC code
#define N 1000006
char s[N];
char sta[N]; int top = 0 ;
int main()
{
// freopen("D:\\垃圾程序存储\\1.txt","r",stdin);
while ( scanf("%s",s) != EOF ){
int slen = strlen(s);
bool fal = 0 ;
rep(i,0,slen-1){
if ( fal ){
break;
}
if ( s[i] == s[slen-1-i] )
fal = 1;
if ( s[i]=='('){
sta[++top] = '(';
}
else {
top--;
if ( top < 0 )
fal = 1;
}
}
if ( fal || top ) cout<<"NO"<<endl;
else cout<<"YES"<<endl;
}
return 0;
}
B题: 语音评测系统(简单)
题解
暴力模拟即可。
AC code
#define N 100006
long long n;long long a[N],b[N],q;
int main()
{
// freopen("D:\\垃圾程序存储\\1.txt","r",stdin);
n = read();
rep(i,1,n) a[i] = read();
rep(i,1,n) b[i] = read();
q = read();
while ( q-- ){
long long num = read();
long long minx = inf;
rep(i,1,n){
if ( minx > (num-a[i])*(num-a[i])+b[i] )
minx = (num-a[i])*(num-a[i])+b[i];
}
printf("%lld ",minx);
}
return 0;
}
C题: 语音评测系统(中等)
题解
暴力模拟即可。
AC code
代码与B题同。
D题: 语音评测系统(困难)
官方题解
注意到每个二次曲线的开口是一样大的,每两个 f 至多只有一个交点。 那么每一个 f 至多只能表示 g 中连续的一段。那么我们就可以只用一个队列来表示g ,复杂度O(n) 。
个人理解
所有的,n个f函数(二次函数),开口方向向上,形状相同(也就是开口大小相同,可以一个函数通过平移得到所有二次函数),此时,我们可以推断,任意两个 f 函数只相交于一点,那么g(x)= min( f(x) )。那么我们可知,g(x)其实是由f函数中的全部,或者几个函数,在这些 f 函数中选取片段,拼接出 g 函数,
AC code
#define N 2000000
typedef long long ll;
using namespace std;
int n, cnt;
ll a[N], b[N], l[N];
double x[N];
int read(){ int p=0, q=1; char ch=getchar(); while (ch<'0' || ch>'9') (ch=='-'?q=-1:0), ch=getchar(); while (ch>='0' && ch<='9') p=p*10+ch-'0', ch=getchar(); return p*q;}
int main(){
n=read();
for (int i=1;i<=n;i++) a[i]=read();
for (int i=1;i<=n;i++) b[i]=read();
int cnt=1;
l[1]=1;
x[1]=-99999999;
for (int i=2;i<=n;i++)
{
int flag=1;
while (cnt)
{
int id=l[cnt];
if ( a[id]==a[i] )
{
if (b[id]>=b[i])
{
cnt--;
continue;
}
flag=0;
break;
}
x[i]=( (double)(b[id]-b[i])/(a[id]-a[i]) + a[i] + a[id] )/2;
if (x[i]<=x[id]) cnt--;
else break;
}
if (!cnt) x[i]=-99999999;
if (flag) l[++cnt]=i;
}
for (int i=read();i;i--)
{
ll xx=read();
int le=1, ri=cnt+1;
while (le<ri-1)
{
int mid=le+ri>>1;
if (x[l[mid]]<=xx) le=mid;
else ri=mid;
}
ll ans=(xx - a[ l[le] ] )*( xx-a[l[le]] )+b[ l[le] ];
printf("%lld%s", ans, (i==1?"\n":" "));
}
return 0;
}
代码解释
cnt :有cnt个F函数组成了G函数,我所有对cnt的修改操作都是为了维护cnt的意义。
l数组:有cnt个F函数,必然有先后顺序,必然有编号,如果,第 i 个 F函数的一部分在G函数里面,那么 i 所对应的输入 F 函数的编号就是 l[i] .
x数组: 有cnt个F函数,他们组成一段G函数,相交于cnt-1个点,第i个交点的x坐标就是x[ i+1 ]。令所有F函数组成G的过程中,我一共枚举了,四种情况。
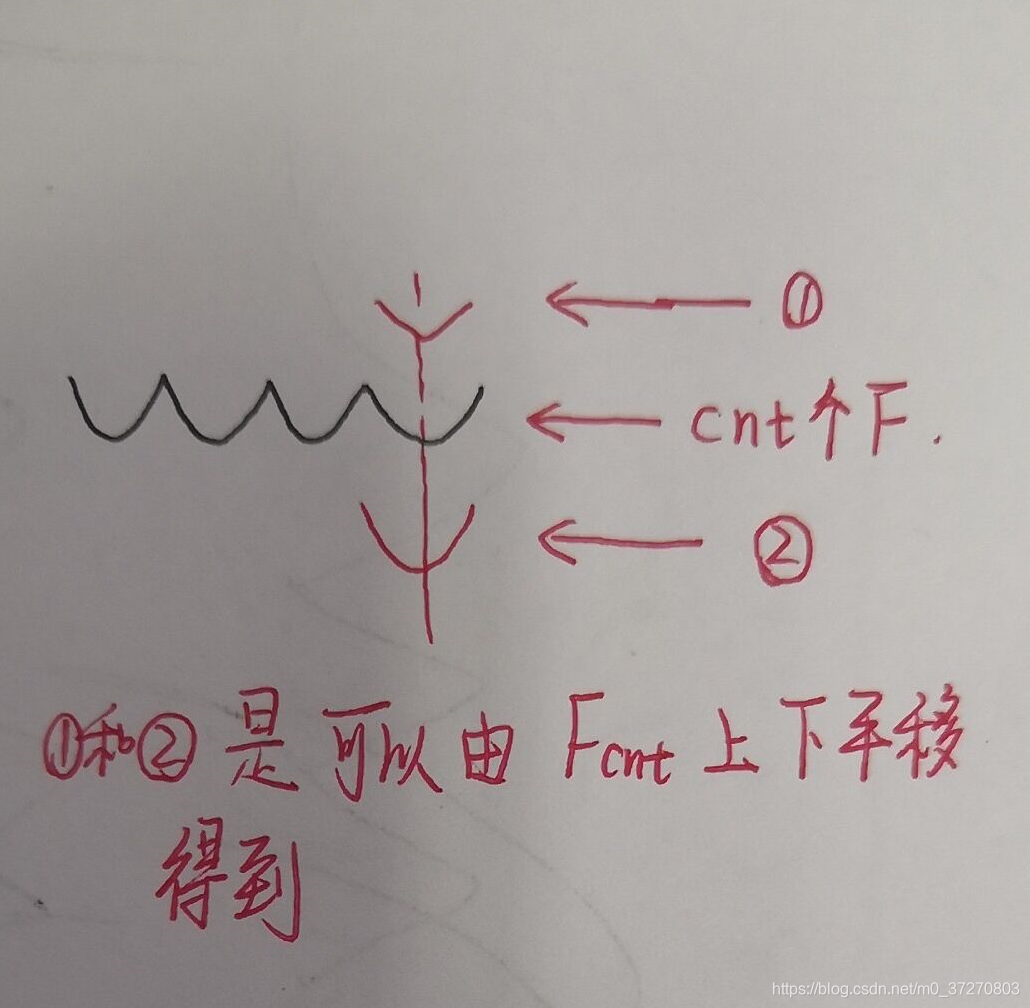
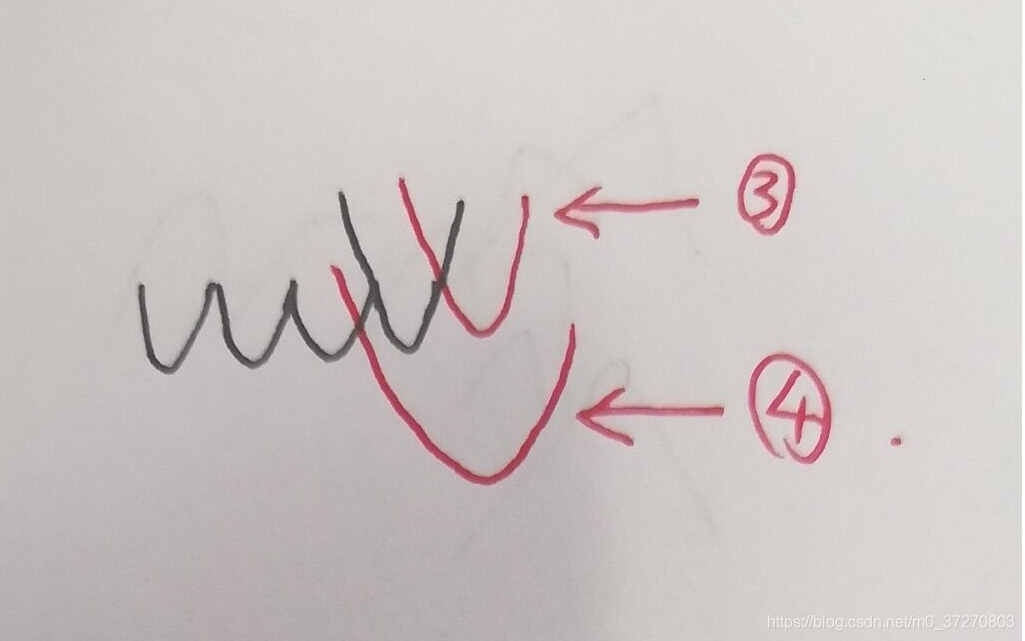








 本文深入解析比赛通道中的算法题目,包括VIPKID大数据黑科技、语音评测系统等多个问题的解决方案,涉及栈、队列、二次函数等数据结构与数学概念,提供AC代码并详细解读。
本文深入解析比赛通道中的算法题目,包括VIPKID大数据黑科技、语音评测系统等多个问题的解决方案,涉及栈、队列、二次函数等数据结构与数学概念,提供AC代码并详细解读。
















 1063
1063

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








