计算智能——蚁群算法

最新推荐文章于 2025-06-01 14:33:56 发布

lzydelyc

最新推荐文章于 2025-06-01 14:33:56 发布

阅读量1.7k

点赞数

CC 4.0 BY-SA版权

本文链接：https://blog.youkuaiyun.com/lzydelyc/article/details/102918999

本文详细介绍了蚁群算法的原理，探讨了信息素重要程度因子、启发函数重要程度因子和信息素挥发因子如何影响算法效果，通过实例展示了不同参数设置下最短路径的计算，并得出了各项参数对算法收敛性和全局搜索能力的影响结论。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

蚁群算法

1.算法原理

蚁群算法是模拟蚂蚁觅食的原理，设计出的一种群集智能算法。蚂蚁在觅食过程中能够在其经过的路径上留下一种称之为信息素的物质，并在觅食过程中能够感知这种物质的强度，并指导自己行动方向，它们总是朝着该物质强度高的方向移动，因此大量蚂蚁组成的集体觅食就表现为一种对信息素的正反馈现象。某一条路径越短，路径上经过的蚂蚁越多，其信息素遗留的也就越多，信息素的浓度也就越高，蚂蚁选择这条路径的几率也就越高，由此构成的正反馈过程，从而逐渐的逼近最优路径，找到最优路径。

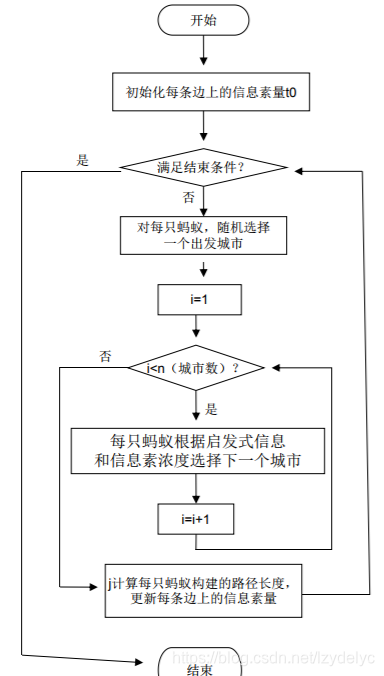
2.基本流程

在这里插入图片描述

3.数据获取

3.1信息素重要程度因子改变时

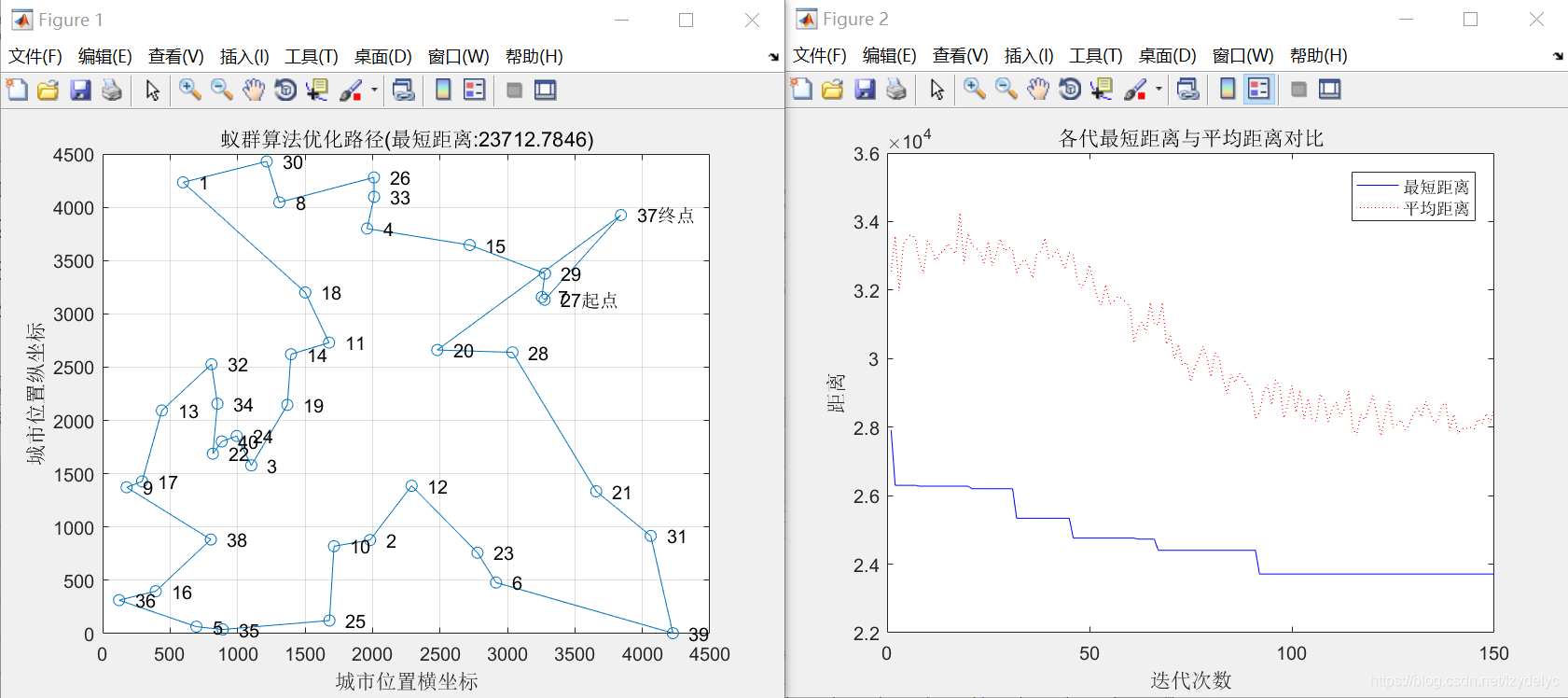
3.1.1
alpha = 1;
beta = 5;
rho = 0.1;
最短距离:23712.7846
最短路径:27 7 29 15 4 33 26 8 30 1 18 11 14 19 3 24 40 22 34 32 13 17 9 38 16 36 5 35 25 10 2 12 23 6 39 31 21 28 20 37 27
在这里插入图片描述
3.1.2
alpha = 3;
beta = 5;
rho = 0.1;
最短距离:24330.1047
最短路径:15 4 33 26 8 30 1 18 11 14 19 24 40 22 3 34 32 13 17 9 38 16 36 5 35 25 10 2 12 23 6 21 31 39 28 20 27 7 29 37 15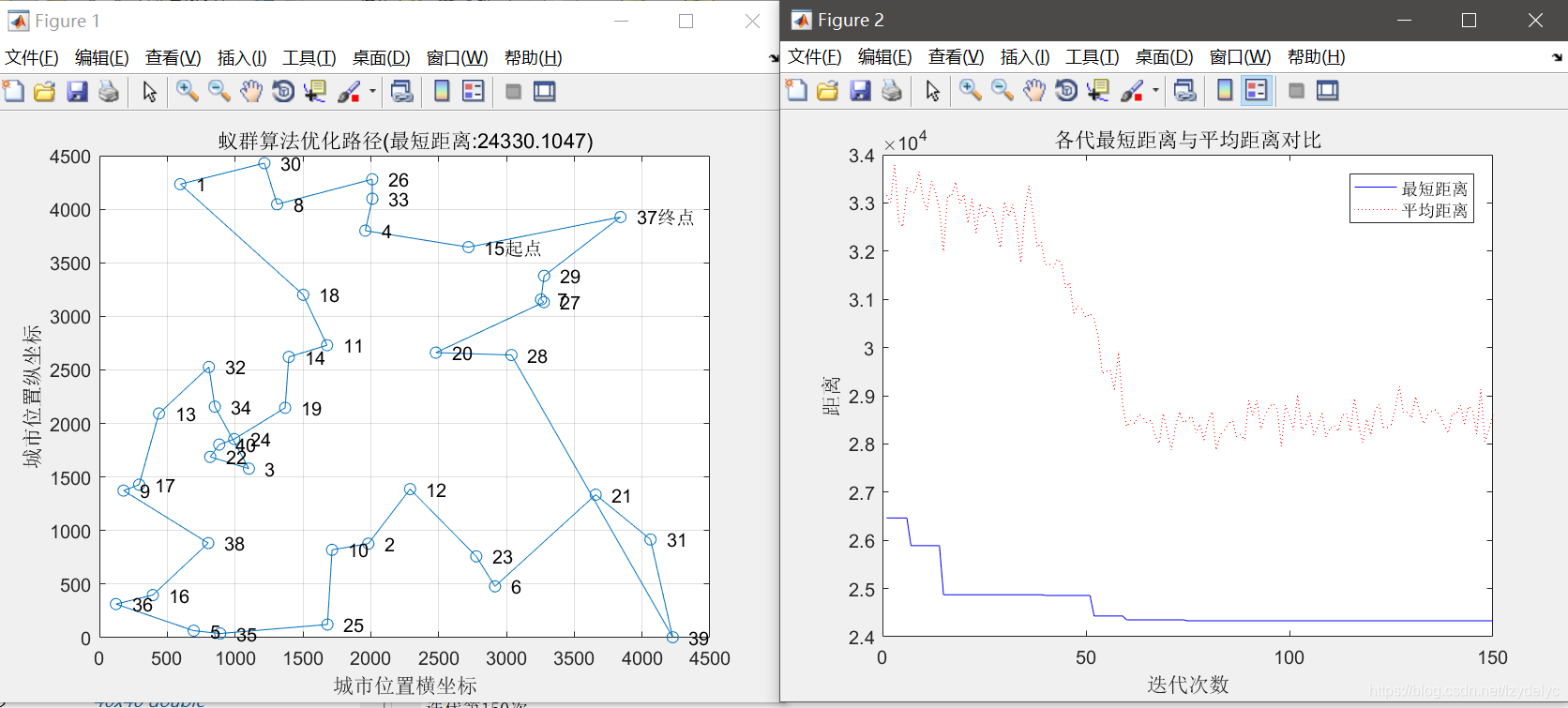
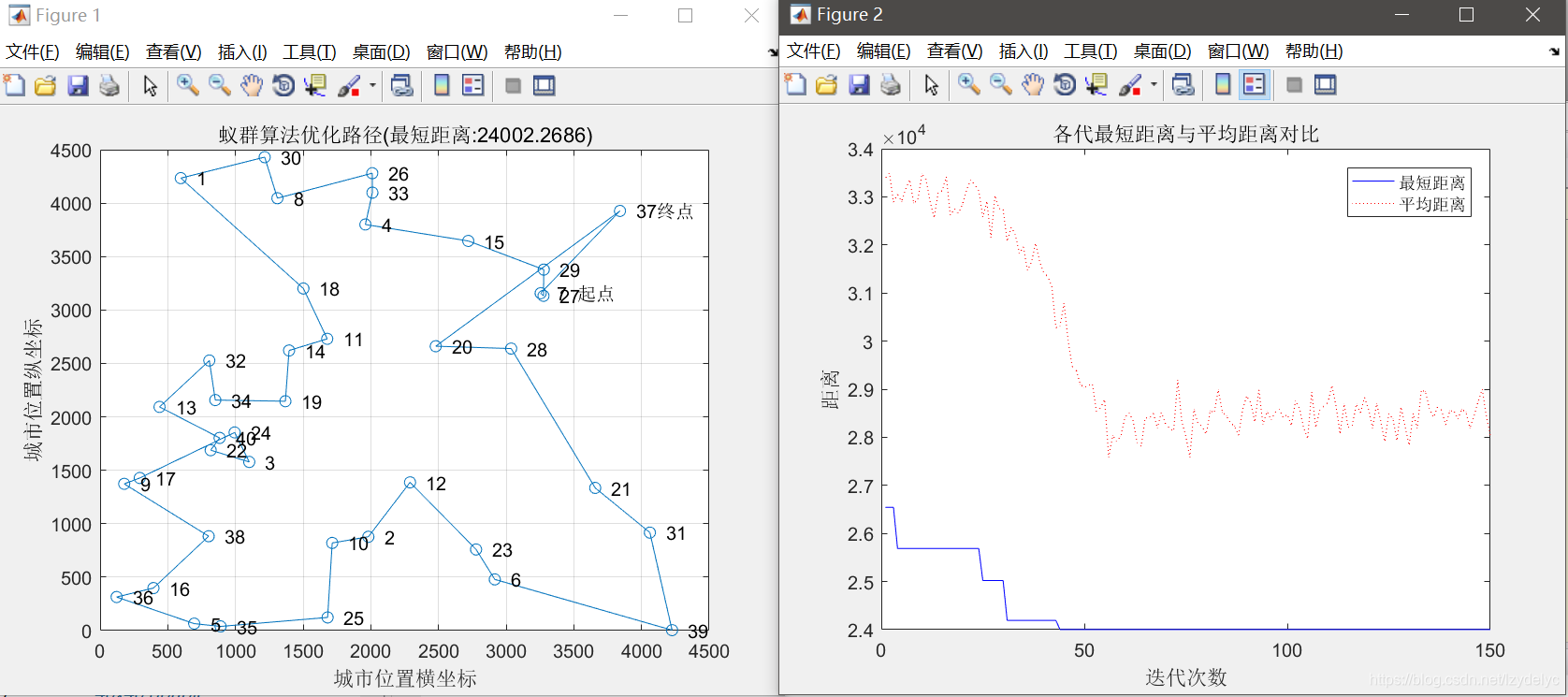
3.1.3
alpha = 5;
beta = 5;
rho = 0.1;
最短距离:24002.2686
最短路径:7 27 29 15 4 33 26 8 30 1 18 11 14 19 34 32 13 40 22 3 24 17 9 38 16 36 5 35 25 10 2 12 23 6 39 31 21 28 20 37 7
在这里插入图片描述

3.2启发函数重要程度因子改变时

3.2.1
alpha = 1;
beta = 5;
rho = 0.1;
最短距离:23712.7846
最短路径:27 7 29 15 4 33 26 8 30 1 18 11 14 19 3 24 40 22 34 32 13 17 9 38 16 36 5 35 25 10 2 12 23 6 39 31 21 28 20 37 27
在这里插入图片描述
3.2.2
alpha = 1;
beta = 4;
rho = 0.1;
最短距离:23163.2512
最短路径:24 40 22 3 34 32 13 17 9 38 16 36 5 35 25 10 2 12 23 6 39 31 21 28 20 7 27 29 37 15 4 33 26 8 30 1 18 11 14 19 24

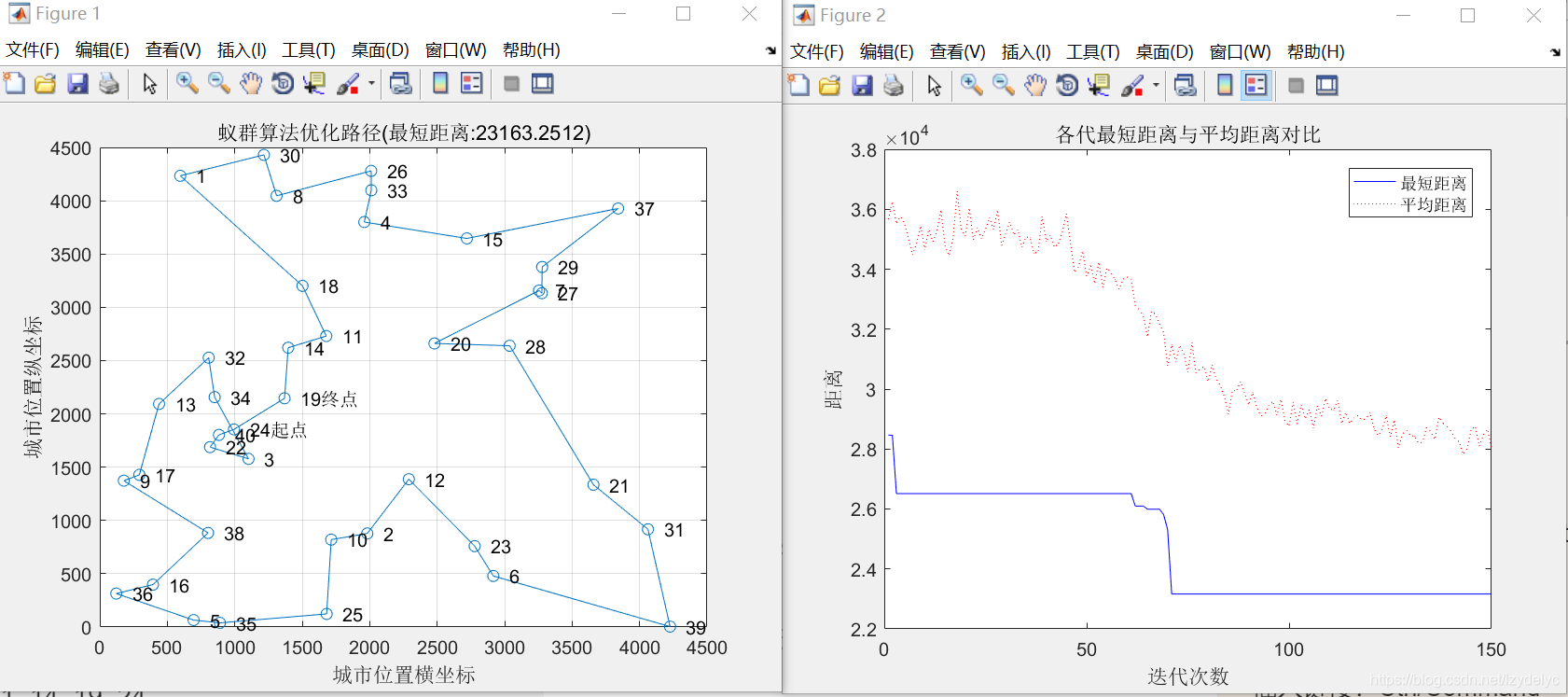
3.2.3
alpha = 1;
beta = 3;
rho = 0.1;
最短距离:23144.2149
最短路径:27 7 29 37 15 4 33 26 8 30 1 18 11 14 19 24 40 22 3 34 32 13 17 9 38 16 36 5 35 25 10 2 12 23 6 39 31 21 28 20 27
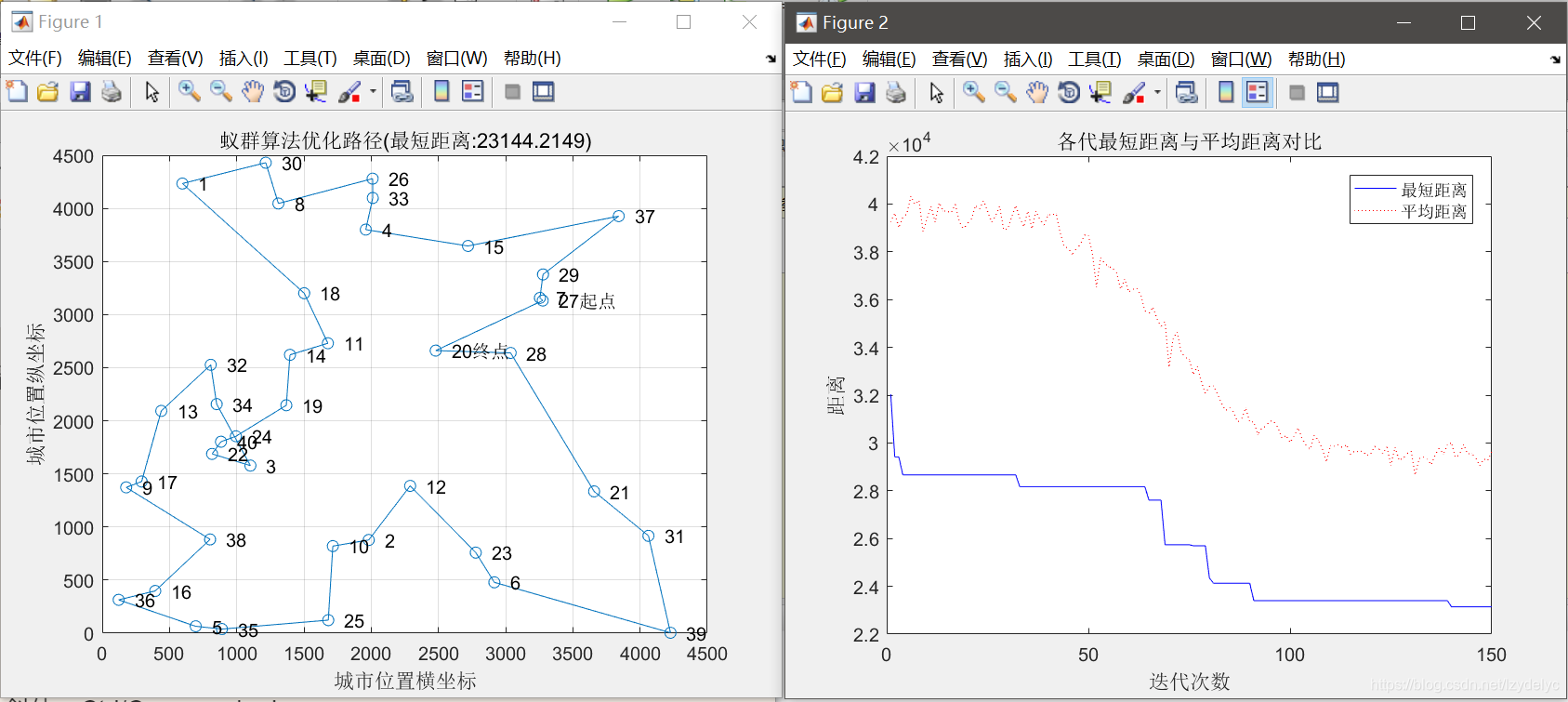
在这里插入图片描述
3.2.4
alpha = 1;
beta = 2;
rho = 0.1;
最短距离:23795.7455
最短路径:20 28 27 7 29 37 15 4 33 26 8 30 1 18 11 14 19 24 40 22 3 34 32 13 17 9 38 16 36 5 35 25 10 2 12 23 6 31 39 21 20

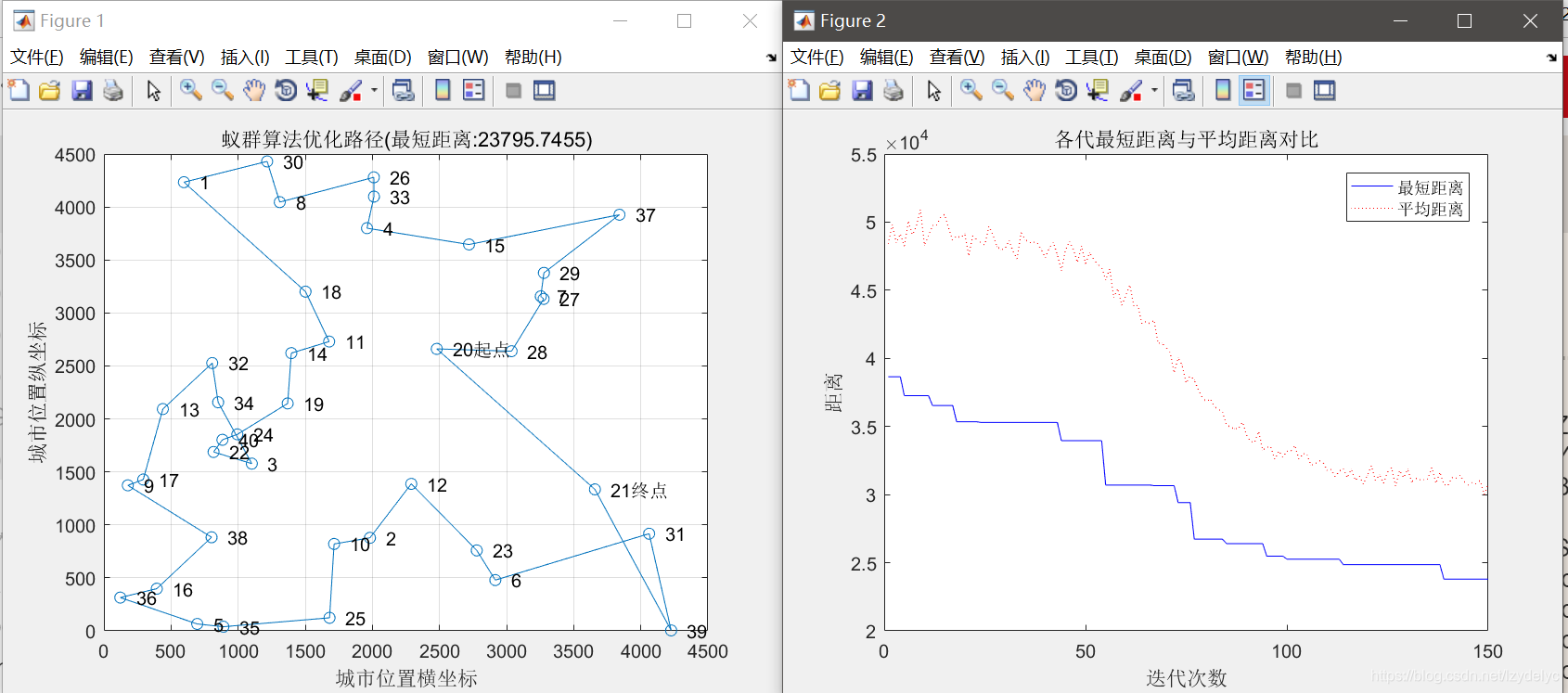
3.3信息素挥发因子改变时

3.3.1
alpha = 1;
beta = 5;
rho = 0.1;
最短距离:23712.7846
最短路径:27 7 29 15 4 33 26 8 30 1 18 11 14 19 3 24 40 22 34 32 13 17 9 38 16 36 5 35 25 10 2 12 23 6 39 31 21 28 20 37 27
在这里插入图片描述
3.3.2
alpha = 1;
beta = 5;
rho = 0.3;
最短距离:23679.5938
最短路径:39 31 21 28 20 37 29 7 27 15 4 33 26 8 30 1 18 11 14 19 24 40 22 3 34 32 13 17 9 38 16 36 5 35 25 10 2 12 23 6 39
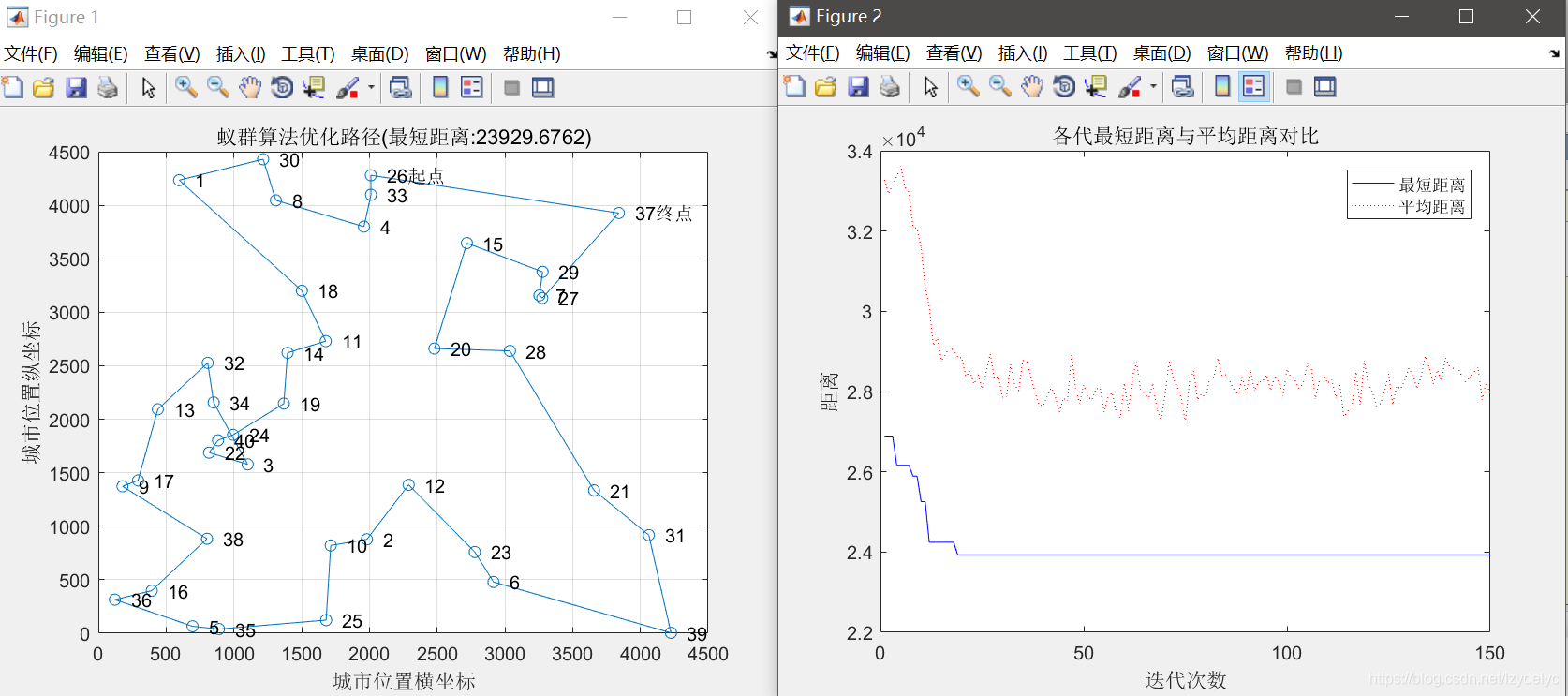
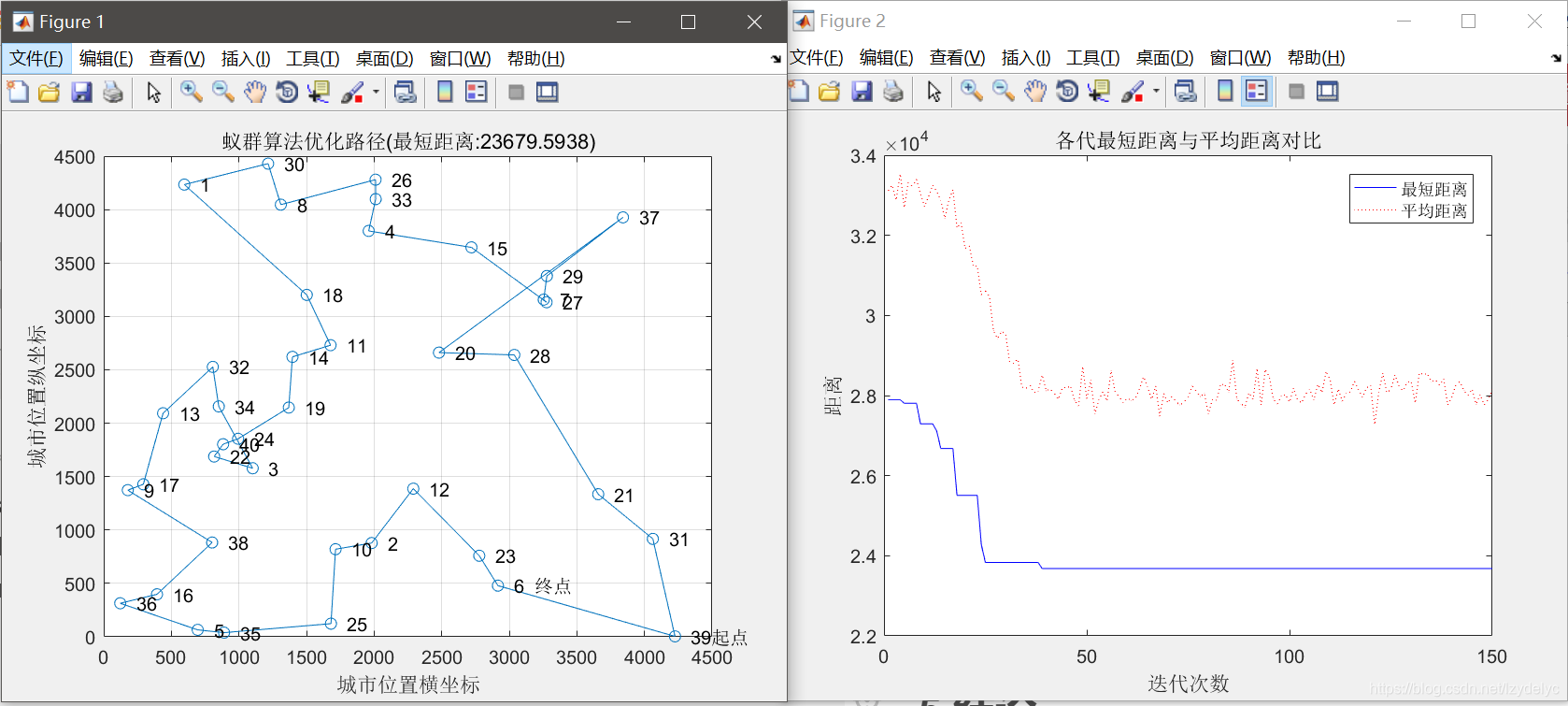3.3.3
alpha = 1;
beta = 5;
rho = 0.6;
最短距离:23929.6762
最短路径:26 33 4 8 30 1 18 11 14 19 24 40 22 3 34 32 13 17 9 38 16 36 5 35 25 10 2 12 23 6 39 31 21 28 20 15 29 7 27 37 26
在这里插入图片描述

4.算法实现（matlab）

4.1
城市40座通过随机函数生成，再将其导入citys.mat中使用
在这里插入图片描述
4.2代码实现

%% 旅行商问题(TSP)优化
%% 清空环境变量
clear all
clc

%% 导入数据
load citys.mat

%% 计算城市间相互距离
fprintf('Computing Distance Matrix... \n');
n = size(citys,1);
D = zeros(n,n);
for i = 1:n
    for j = 1:n
        if i ~= j
            D(i,j) = sqrt(sum((citys(i,:) - citys(j,:)).^2));
        else
            D(i,j) = 1e-4;      
        end
    end    
end

%% 初始化参数
fprintf('Initializing Parameters... \n');
m = 50;                              % 蚂蚁数量
alpha = 1;                           % 信息素重要程度因子
beta = 5;                            % 启发函数重要程度因子
rho = 0.6;