文章详细阐述了递推和递归的概念，通过数列的例子解释了两者的区别和联系。递推通常用循环实现，效率较高，而递归则用函数实现，可能消耗更多时间和空间。接着，文章提供了从循环控制语句转换到递推算法的示例，计算阶乘和阶乘之和，并进一步展示了如何用递归算法解决相同问题。最后，给出了斐波那契数列的递推和递归解法，以及一个关于桃子数量的递推和递归问题。
1.递推和递归的概念
1、递推算法：
- 打个比方：以数列为例，我们已经知道或者观察出数列的后一项是前一项或者前几项的某个固定的函数关系（即递推公式），并且知道数列的第一项或者前几项。如果不通过求数列通项公式的方式，问：该如何求数列的第n项，以及前n项的和呢？
- 递推的特点：由低到高，由初值到终值，由简单到复杂。从初值出发，确定递推公式，每次重复都在旧值的基础上推出新值。
2、递归算法：
- 打个比方：还是数列的例子：“已知数列的某一项或几项的值，并且知道数列的递推公式，该如何求数列的第n项呢”。我们换个思路，既然我们都已经知道了递推公式，何不直接将递推公式写成一个函数？比方说我们用 f(n)代表数列的通项公式，然后递推公式比方说是 f(n) = f(n-1) + f(n-2)，那么我们就可以构造一个函数F(n)，在函数体内部，函数会调用自身，即F(n) = F(n-1) + F(n-2)。然后我们不是知道了函数的某一项或者某几项的值吗，那么，我们可以在递归函数F(n)中做判断，当我们调用到这些确定的项时，就结束函数内部的自身调用。函数的返回值就是我们最后想要得到的结果。
- 递归的特点：由高到低，由终值到初值，由复杂到简单。递归是算法自我调用的过程，先将问题难度由高到低进行分解，然后由低到高解决它。
3、递推法和递归法的区别和联系：
- 递归算法一般用函数实现，递推算法一般用循环实现，二者表达的其实是一个意思。
- 在简单问题中，递推法能解决的，使用递推法效率比使用递归法效率要高。因为，递归缺点是有太多函数调用，运行时耗费时间和空间。
- 递归过程要有一个递归出口，递归出口也就是递推入口，递归出口需要在一开始进入函数时就确定，递推入口需要在进入循环前就确定。
2.从循环控制语句到递推算法
我们在学习循环控制语句的时候，我们的循环变量都比较简单：
- 有的是只表示循环次数的变量，它们在循环末尾通过自加减运算改变自身的值；
- 有的是参与简单循环运算的变量，它们在每次循环末尾通过赋值运算来改变其他循环变量的值，来方便下一次运算；
- 有的是用于循环遍历的变量，它们在已知的结果范围内变化。
例题1：用循环嵌套计算阶乘n!，以及阶乘之和：1! + 2! + ········· + n!
- 思路：
1. 输入一个正整数n /* 计算n! */ 2. for循环，循环变量i从1开始，<=n 时进入循环 2.1 改变循环变量item的值，item = item * i;（item最后保存n!） 3. 打印n!的值 /* 计算1!+...+n! */ 4. for循环，循环变量i从1开始，<=n 时进入循环 4.1 进入内层循环前令item=1（item后面表示第i项，即i!） /* 计算级数1!+...+n!中第i项 */ 4.2 for循环，循环变量j从1开始，<=i 时进入循环 4.2.1 改变循环变量item，item = item * j;（这里可以看出为什么写4.1） 4.2 改变用于求和的循环变量sum，sum=sum+第i项 5. 打印sum的值 - 代码：
#include <stdio.h> int main(int argc, char const *argv[]) { int i, j; //i是外层循环变量，j是内层循环变量 int n; //用户输入值 int sum = 0; //求和循环变量 int item = 1; //用来计算n!的循环变量 puts("请输入一个正整数"); scanf("%d", &n); for ( i = 1; i <=n ; i++){ item = item * i; } printf("%d!=%d\n", n, item); for ( i = 1; i <= n; i++){ item = 1; for ( j = 1; j <= i; j++){ item = item * j; } sum = sum + item; } printf("1!+...+%d!=%d\n", n, sum); return 0; }
例题2：用递推算法计算阶乘n!，以及阶乘之和：1! + 2! + ········· + n!
- 思路：我们发现递推公式是“第n项 = 第n-1项 × n”
1. 输入一个正整数n /* 计算n!和1!+...+n! */ 2. 设置递推入口: item_0 = 1; 3. for循环，循环变量i从1开始，<=n 时进入循环 3.1 用递推公式：“第n项=第n-1项×n”，改变循环变量item的值：item_1 = item_0 * i; 3.2 改变用于求和的循环变量sum 3.3 改变循环变量item_0的值，上一次的item_1作为下一次的item_0 4. 打印n!的值 5. 打印sum的值 - 代码：实际上item_0可以和item_1写成一项，这里写成两项是为了方便理解，实际写代码时两者皆可
#include <stdio.h> int main(int argc, char const *argv[]) { int i; //循环变量 int n; //用户输入值 int sum = 0; //求和循环变量 int item_1; //用于递推的循环变量，代表第i项 int item_0 = 1; //用于递推的循环变量，代表第i-1项 puts("请输入一个正整数"); scanf("%d", &n); for( i = 1; i <= n; i++){ item_1 = item_0 * i; sum = sum + item_1; item_0 = item_1; } printf("%d!=%d\n", n, item_1); printf("1!+...+%d!=%d\n", n, sum); return 0; }
3.从函数调用到递归算法
例题3：用递归算法计算阶乘n!，以及阶乘之和：1! + 2! + ········· + n!
- 思路：函数只能返回一个值
f1. 定义求阶乘n!的递归函数: int factorial(int n){... return item;} f1.1 设置递归出口，判断n是否等于1 f1.1.1 如果是， 那么，令出口值item=1 f1.1.2 否则， 那么，写递推函数：item=factorial(n-1)*n; f1.2 返回结果item 1. 输入一个正整数n 2. 使用函数f1获取n!，并打印n!的值 3. for循环，循环变量i从1开始，<=n 时进入循环 3.1 改变用于求和的循环变量sum: sum=sum+第i项 4. 打印sum的值 - 代码：
#include <stdio.h> int factorial(int n){ int item; if (n == 1){ item = 1; }else{ item = factorial(n-1) * n; } return item; } int main(int argc, char const *argv[]) { int n; //用户输入的值 int sum = 0; //1!+...+n!的和 int i; //循环变量 puts("请输入一个正整数"); scanf("%d", &n); printf("%d!=%d\n", n, factorial(n)); for ( i = 1; i <= n; i++){ sum = sum + factorial(i); } printf("1!+...+%d!=%d\n", n, sum); return 0; }
4.习题
习题1：已知斐波那契数列的递推公式为：F（0）= 0；F（1）= 1；F（n）= F（n-1）+ F（n-2）。容易看出本题用递归法容易求解，问：用递推法如何求解？
- 思路：用递推法的时候，循环时涉及到三个变量，我们秉承着先计算再改变循环变量的思路，在改变循环变量时，需要注意书写次序，这与我们之前练习GCD算法时一样，因此注意以下步骤4.2和4.3不能对调。
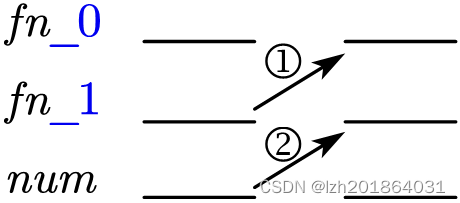
1. 输入整数n（第几项） 2. 设置递推入口：fn_0 = 0; fn_1 = 1; 3. 判断n是否为0（因为第0项比较特殊） 3.1 如果是， 那么，num = 0;（num表示斐波那契数列的第n项） 4. for循环，循环变量i从1开始，<=n 时进入循环 4.1 用递推公式：“第n项=第n-1项+第n-2项”，改变循环变量num的值:num=fn_0+fn_1; 4.2 改变循环变量fn_0的值，上一次fn_1作为下一次的fn_0 4.3 改变循环变量fn_1的值，上一次num作为下一次的fn_1 5. 打印num的值 - 代码：
#include <stdio.h> int main(int argc, char const *argv[]) { int n; //用户输入的值 int num; //斐波那契数列第n项的值 int i; //循环变量 int fn_0 = 0, fn_1 = 1; //求斐波那契数列第n项时，用于递推的循环变量 printf("请输入斐波那契数列的第几项(>=0):\n"); scanf("%d", &n); if (n == 0){ num = 0; } for ( i = 1; i <= n; i++){ num = fn_0 + fn_1; fn_0 = fn_1; fn_1 = num; } printf("斐波那契数列的第%d项是:%d\n", n, num); return 0; }
习题2：猴子每天都吃掉上一天剩下桃子总数的一半多一个，已知第6天只剩一个桃子，问第1天有几个桃子？分别用递推法和递归法实现。
- 思路：我们用x_1代表今天的桃子数，用x_0代表昨天的桃子数，由于今天吃掉了昨天的一半多一个，因此今天还剩下 x_1 = x_0 - (x_0 / 2 + 1)个桃子，化简得x_1 = x_0 / 2 - 1，故递推公式为 x_0 = (x_1 + 1) * 2这里用递推算法时，我们也可以只定义一个变量x。
/* 递推法实现 */ 1. 设置递推入口：x_1 = 1; 2. for循环，循环5次即可 2.1 用递推公式：“昨天的桃子数=(今天的+1)*2”，改变循环变量x_0的值:x_0=(x_1+1)*2 2.2 改变循环变量x_1的值，上次的x_0作为下次的x_1 3. 打印第6天的桃子数x_0 /* 递归法实现 */ f1. 定义求第一天桃子数的递归函数：int peach(int day){... return x_0;} f1.1 设置递归出口，判断day是够等于6 f1.1.1 如果是， 那么，令出口值x_0=1 f1.1.2 否则，判断day是否介于0和6之间 f1.1.2.1 如果是， 那么，写递推函数：x_0=(peach(day+1)+1)*2 f1.1.3 否则，打印出错 f1.2 返回结果x_0 1. 使用函数f1获取第一天的桃子数，并打印 - 代码：
/* 递推法实现 */ #include <stdio.h> int main(int argc, char const *argv[]) { int x_0; //用于递推的循环变量，代表昨天的桃子数 int x_1 = 1; //用于递推的循环变量，代表今天的桃子数 int i; //循环变量 for ( i = 1; i < 6; i++){ //注意循环5次就够了 x_0 = (x_1 + 1) * 2; x_1 = x_0; } printf("第1天的桃子数是%d个\n", x_0); return 0; } /* 递归法实现 */ #include <stdio.h> int peach(int day) { int x_0; if (day == 6){ x_0 = 1; }else if (day > 0 && day < 6){ x_0 = (peach(day+1) + 1) * 2; }else{ puts("wrong"); } return x_0; } int main(int argc, char const *argv[]) { printf("第1天的桃子数时%d个\n", peach(1)); return 0; }
扫一扫
3896
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
