【机器学习】琴生不等式(Jensen’s inequality):
凸/凹函数概述
“琴生不等式描述的是积分的凸/凹函数值和凸/凹函数的积分值间的关系。”
以上定义来自维基百科,虽然晦涩难懂,但是我们可以得出结论:在学习琴生不等式的时,必须要对与之相关凸/凹函数有一个大概的认识。
什么是凸/凹函数?
“凸函数是具有如下特性的一个定义在某个向量空间的凸子集CCC(区间)上的实值函数fff:对其定义域CCC上的任意两点x1x_1x1, x2x_2x2,总有f(x1+x22)≤f(x1)+f(x2)2f(\frac{x_1+x_2}{2})\leq\frac{f(x_1)+f(x_2)}{2}f(2x1+x2)≤2f(x1)+f(x2)。”
“凹函数是具有如下特性的一个定义在某个向量空间的凹子集CCC(区间)上的实值函数fff:对其定义域CCC上的任意两点x1x_1x1, x2x_2x2,总有f(x1+x22)≥f(x1)+f(x2)2f(\frac{x_1+x_2}{2})\geq\frac{f(x_1)+f(x_2)}{2}f(2x1+x2)≥2f(x1)+f(x2)。”
以上定义依然来自维基百科,依然晦涩难懂,重要的是了解以下结论。
结论一:凸/凹函数的二阶导数恒大于/小于零
结论二:一个凸/凹函数上任意两点所作割线一定在这两点之间的函数图像的上/下方
琴生不等式概述
1、若f(x)f(x)f(x)是区间(a,b)(a,b)(a,b)上的凸函数,则对任意的x1,x2,x3, ......,xn∈(a,b)x_1,x_2,x_3,\ ......,x_n\in(a,b)x1,x2,x3, ......,xn∈(a,b),有不等式:
f(x1+x2+x3+......+xnn)≤f(x1)+f(x2)+f(x3)+......+f(xn)nf(\frac{x_1+x_2+x_3+......+x_n}{n})\leq\frac{f(x_1)+f(x_2)+f(x_3)+......+f(x_n)}{n}f(nx1+x2+x3+......+xn)≤nf(x1)+f(x2)+f(x3)+......+f(xn)
有当且仅当x1=x2=x3=......=xnx_1=x_2=x_3=......=x_nx1=x2=x3=......=xn时等号成立。
2、若f(x)f(x)f(x)是区间(a,b)(a,b)(a,b)上的凹函数,则对任意的x1,x2,x3, ......,xn∈(a,b)x_1,x_2,x_{3,\ }......,x_n\in(a,b)x1,x2,x3, ......,xn∈(a,b),有不等式:
f(x1+x2+x3+......+xnn)≥f(x1)+f(x2)+f(x3)+......+f(xn)nf(\frac{x_1+x_2+x_3+......+x_n}{n})\geq\frac{f(x_1)+f(x_2)+f(x_3)+......+f(x_n)}{n}f(nx1+x2+x3+......+xn)≥nf(x1)+f(x2)+f(x3)+......+f(xn)
有当且仅当x1=x2=x3=......=xnx_1=x_2 =x_3=......=x_nx1=x2=x3=......=xn时等号成立。
3、若f(x)f(x)f(x)是区间(a,b)(a,b)(a,b)上的凸函数,则对任意的x1,x2,x3......,xn∈(a,b)x_1,x_2,x_3......,x_n \in(a,b)x1,x2,x3......,xn∈(a,b),∑i=1nan=1\sum_{i=1}^{n}a_n = 1∑i=1nan=1,a1,a2,a3......ana_1,a_2,a_3......a_na1,a2,a3......an为正数,则有:f(a1x1+a2x2+a3x3+......+anxn)≤f(a1x1)+f(a2x2)+f(a3x3)+......+f(anxn) (α){f(a}_1x_1+a_2x_2+a_3x_3+......+a_nx_n)\leq f(a_1x_1)+f(a_2x_2)+f(a_3x_3)+......+f(a_nx_n)\ \ \ \ \ \ \ \ \ \ (\alpha)f(a1x1+a2x2+a3x3+......+anxn)≤f(a1x1)+f(a2x2)+f(a3x3)+......+f(anxn) (α)
4、若f(x)f(x)f(x)是区间(a,b)(a,b)(a,b)上的凹函数,则对任意的x1,x2,x3......,xn∈(a,b)x_1,x_2,x_3......,x_n \in(a,b)x1,x2,x3......,xn∈(a,b),∑i=1nan=1\sum_{i=1}^{n}a_n = 1∑i=1nan=1,a1,a2,a3......ana_1,a_2,a_3......a_na1,a2,a3......an为正数,则有:f(a1x1+a2x2+a3x3+......+anxn)≥f(a1x1)+f(a2x2)+f(a3x3)+......+f(anxn) (β){f(a}_1x_1+a_2x_2+a_3x_3+......+a_nx_n)\geq f(a_1x_1)+f(a_2x_2)+f(a_3x_3)+......+f(a_nx_n)\ \ \ \ \ \ \ \ \ \ (\beta)f(a1x1+a2x2+a3x3+......+anxn)≥f(a1x1)+f(a2x2)+f(a3x3)+......+f(anxn) (β)
琴生不等式在概率学中的应用
通过观察(α)(\alpha)(α)式左式(a1x1+a2x2+a3x3+......+anxn){(a}_1x_1+a_2x_2+a_3x_3+......+a_nx_n)(a1x1+a2x2+a3x3+......+anxn),我们知道∑i=1nan=1\sum_{i=1}^{n}a_n = 1∑i=1nan=1。符合随机变量X的概率方程。因此该式所表达的正好是随机变量XXX的期望,E(X)E(X)E(X)。
我们重写(α)(\alpha)(α)式,其中ppp代表probability:
f(p1x1+p2x2+p3x3+......+pnxn)≤f(p1x1)+f(p2x2)+f(p3x3)+......+f(pnxn){f(p}_1x_1+p_2x_2+p_3x_3+......+p_nx_n)\le f(p_1x_1)+f(p_2x_2)+f(p_3x_3)+......+f(p_nx_n)f(p1x1+p2x2+p3x3+......+pnxn)≤f(p1x1)+f(p2x2)+f(p3x3)+......+f(pnxn)
左式=f(∑i=1npnxn)=f(E(X))=f(\sum_{i=1}^{n}p_nx_n)=f(E(X))=f(∑i=1npnxn)=f(E(X))
右式=∑i=1npnf(xi)=E(f(X))=\sum_{i=1}^{n}{p_nf(x_i})=E(f(X))=∑i=1npnf(xi)=E(f(X))
综上且同理(β)(\beta)(β),我们可以得出以下结论。
结论三:对于凸函数,随机变量X∈[x1,xn]X∈[x_1,x_n]X∈[x1,xn],则在[x1,xn][x_1,x_n][x1,xn]区间内任意一点,f(E(x))≤E(f(x))f(E(x))\leq E(f(x))f(E(x))≤E(f(x))
结论四:对于凹函数,随机变量X∈[x1,xn]X∈[x_1,x_n]X∈[x1,xn],则在[x1,xn][x_1,x_n][x1,xn]区间内任意一点,f(E(x))≥E(f(x))f(E(x))\geq E(f(x))f(E(x))≥E(f(x))
琴生不等式的证明
我们可以用以下一般式来表达琴生不等式(以凸函数为例):
f(θx1+(1−θ)x2)≤θf(x1)+(1−θ)f(x2);θ∈[0,1]f(\theta x_1+(1-\theta)x_2)\le\theta f(x_1)+(1-\theta)f(x_2);\theta∈[0,1]f(θx1+(1−θ)x2)≤θf(x1)+(1−θ)f(x2);θ∈[0,1]
则:
f(x2−θ(x2−x1))≤f(x2)−θ(f(x2)−f(x1));θ∈[0,1]f(x_2-\theta(x_2-x_1))\le f(x_2)-\theta(f(x_2)-f(x_1));\theta∈[0,1]f(x2−θ(x2−x1))≤f(x2)−θ(f(x2)−f(x1));θ∈[0,1]
等式两边都只与θ\thetaθ有关,并且变化比例相同(下面给出证明)。
设x∗=x2−θ(x2−x1),x∗∈[x1,x2]x^*=x_2-\theta\left(x_2-x_1\right), x^*∈[x_1,x_2]x∗=x2−θ(x2−x1),x∗∈[x1,x2]
设f(x)∗=f(x2)−θ(f(x2)−f(x1)),f(x)∗∈[f(x1),f(x2)]f(x)^*=f\left(x_2\right)-\theta(f\left(x_2\right)-f(x_1)), f(x)^*∈[f\left(x_1\right),f\left(x_2\right)]f(x)∗=f(x2)−θ(f(x2)−f(x1)),f(x)∗∈[f(x1),f(x2)]
只需证明在下图中,lqlp=lalb\frac{l_q}{l_p}=\frac{l_a}{l_b}lplq=lbla 即可。
lqlp=x2−[x2−θ(x2−x1)][x2−θ(x2−x1)]−x1)=θ1−θ\frac{l_q}{l_p}=\frac{x_2-[x_2-θ(x_2-x_1)]}{[x_2-θ(x_2-x_1)]-x_1)}=\frac{θ}{1-θ}lplq=[x2−θ(x2−x1)]−x1)x2−[x2−θ(x2−x1)]=1−θθ
lalb=f(x2)−[f(x2)−θ(f(x2)−f(x1))][f(x2)−θ(f(x2)−f(x1))]−f(x1)=θ1−θ\frac{l_a}{l_b}=\frac{f(x_2)-[f(x_2)-θ(f(x_2)-f(x_1))]}{[f(x_2)-θ(f(x_2)-f(x_1))]-f(x_1)}=\frac{θ}{1-θ}lbla=[f(x2)−θ(f(x2)−f(x1))]−f(x1)f(x2)−[f(x2)−θ(f(x2)−f(x1))]=1−θθ
证毕
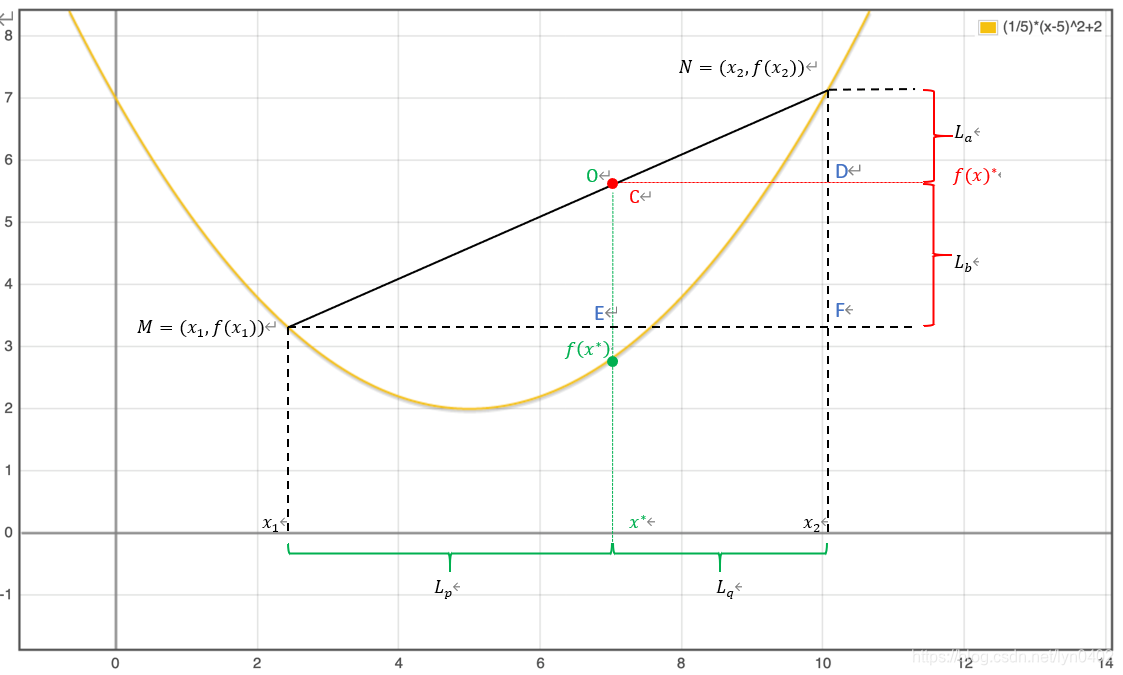
上图所示,正是琴生不等式在凸函数上的证明:在随机变量x∗∈[x1,x2]x^*∈[x_1,x_2]x∗∈[x1,x2]的这个区间内任意一点向X轴引垂线,f(x∗) ≤ f(x)∗f\left(x^*\right)\ \le\ f(x)^*f(x∗) ≤ f(x)∗恒成立。
为什么非要强调是在同一条垂线上f(x∗) ≤ f(x)∗f\left(x_*\right)\ \le\ f(x)^*f(x∗) ≤ f(x)∗呢,因为如果无法证明是在同一垂线上满足f(x∗) ≤ f(x)∗f\left(x^*\right)\ \le\ f(x)^*f(x∗) ≤ f(x)∗, 那么琴生不等式的≤\le≤就不一定成立。
下面给出f(x∗)f\left(x^*\right)f(x∗)与 f(x)∗\ f(x)^* f(x)∗在一条垂线上的证明,证明两点是在同一条垂线上(采用反证法):
首先,过f(x)∗f(x)^*f(x)∗某点做一条X轴的平行线,交MN于点C,则得到∆NCD∗≅∆NMF∆ NCD^*≅∆ NMF∆NCD∗≅∆NMF,根据相似三角形定义,可得ab=NCCM\frac{a}{b}=\frac{NC}{CM}ba=CMNC;
其次,过x∗x^*x∗向Y轴作平行线,交MN于点O,则得到∆MOE≅∆MNF∆ MOE≅∆ MNF∆MOE≅∆MNF,相似三角形, 可证得, qp=NOOM\frac{q}{p}=\frac{NO}{OM}pq=OMNO。
接下, 只需要证明lqlp=lalb\frac{l_q}{l_p}=\frac{l_a}{l_b}lplq=lbla即可, 在上一证明中,我们已经证得该结论,这里就不再做赘述。
综上所证: NCCM=NOOM\frac{NC}{CM}=\frac{NO}{OM}CMNC=OMNO,故点C于点O属于同一点。
注意 琴生不等式等号成立的条件:
只有当x1与x2x_1与x_2x1与x2重合,导致随机变量x∗x^*x∗变为一个定数,MN最终会成为凸函数上一个点,等号成立。





 琴生不等式是关于凸/凹函数的重要性质,它在概率论中有广泛应用。文章介绍了凸/凹函数的概念,然后详细阐述了琴生不等式的定义和证明,并探讨了其在随机变量期望值上的不等式关系。
琴生不等式是关于凸/凹函数的重要性质,它在概率论中有广泛应用。文章介绍了凸/凹函数的概念,然后详细阐述了琴生不等式的定义和证明,并探讨了其在随机变量期望值上的不等式关系。

















 968
968

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








