答案---19

感谢洛谷的猪哥

peaneevall_kalaa和未来姚班zyl

先玩会儿坚果保龄球

把每个僵尸建立 33 个点，表示从哪个方向（水平/左上/左下）打入的，点之间如果打到点 xx 的坚果能滚到点 yy 那么 (x,y)(x,y) 连一条边，题意转化为，动态删点，求最长路。

直接模拟可以获得 2020 至 50pts50pts。

进一步发现，如果去掉表示水平的边，并且将 11 号轨和 nn 号轨上的点只拆点成一个方向，那么每个点的出度入度都 ≤1≤1，图转化为一堆链。

考虑删除点的过程。

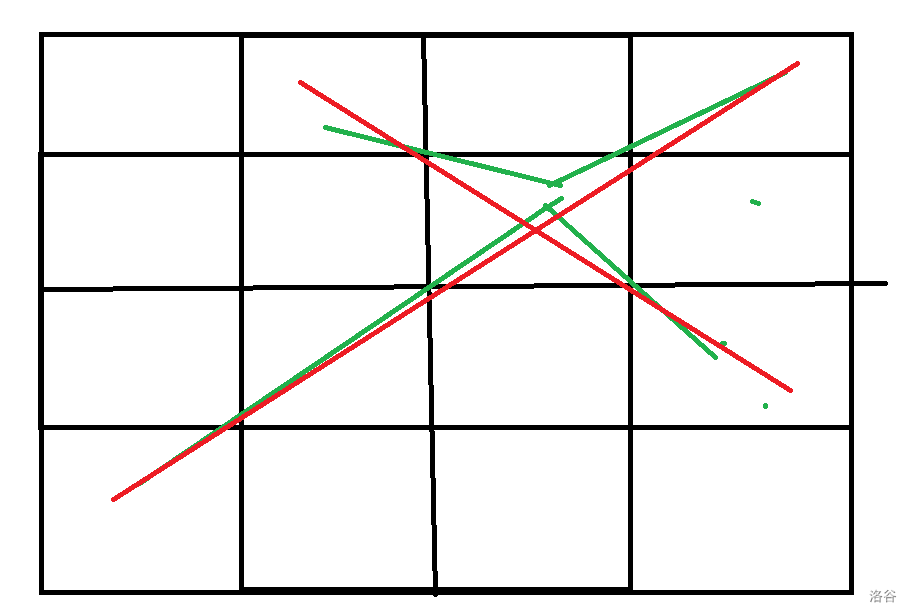
删除第二行第三列的僵尸会使绿线的轨迹变成红线的轨迹，发现就是交换了从左下打入的和左上打入的出边，然后前驱直接连向后继跳过该点。

特别的，如果是 11 号轨或 nn 号轨，前驱直接连向后继跳过该点即可。

怎么判断从最初哪个点打入？如果该点是水平轨道上的从左往右第一个点且打入后方向正确则可以打入。

每次删掉点之后可以打入的点的改变也是 O(1)O(1) 量级的。

在实现上，初始先把图建出来，图的建立方式可以画画轨迹理解一下。

于是，对于每根链可以使用平衡树维护，链的打入点就是从左往右第一个能打入的点（即不用维护链上每一个可以打入的点），每次找最长链可以用一个堆维护二元组 (ans,id)(ans,id) 表示答案和打入的点，每次拿出二元组时判定一下二元组信息是否正确，每次删点时放入新的二元组即可。

我代码因为调试所以显得很长很抽象，实际上是很好写的，我的代码实际上只有 3kb3kb 左右。

如果你在 lojloj 上 WA on #9WA on #9 且行判定有误，且你写的是堆加判定合法代替可删堆，那么你可能在判定合法时没有判定行号。

题目大意

有一个 nn 行的网格图，上面有 mm 个僵尸。

你可以选择一行扔出一个坚果，坚果会沿着这行水平滚出。

如果撞到了一个僵尸，则坚果会改变运动方向，如果水平撞上，则如果在前 n22n​ 行，坚果就会向右下 45°45° 方向滚出，否则向右上 45°45° 方向滚出。如果是以斜着的方向撞上，则会在这两种方向中切换。然后，这个僵尸就被击倒了，并不会再出现在网格图上。

出题人要选一行扔出坚果，满足能击倒最多的僵尸的前提下编号最小。请你模拟 kk 轮这样的操作，每轮输出扔出的行编号和击倒的僵尸数目。

题目分析

这种较为复杂的限制，往往用图论建模来描绘。

将每个点拆点，分为左上和左下两个点。然后连向往那个方向出发后会碰到的第一个点。很容易发现，图由若干条链构成。

如果一个僵尸被击倒，则相当于这个地方不会再改变方向。只需要将两条链在此处断开然后接到正确的位置。

考虑用平衡树维护这些链，map 维护每一行出发会碰到的第一个僵尸，称这些僵尸为关键僵尸，显然我们的链只需要维护最靠左端的关键僵尸。然后用线段树维护一下每一行扔出去会击倒多少僵尸就可以了。

复杂度 O((m+k)log⁡m)O((m+k)logm)。

到这都还是蓝题水平，但开始扣代码就知道这题有多 Hard 了。

#include<bits/stdc++.h>
#define ll long long
#define L(x) t[x].l
#define R(x) t[x].r
#define mid (l+r>>1)
#define lc x<<1,l,mid
#define rc x<<1|1,mid+1,r
#define OK Ll<=l&&r<=Rr
#define Root 1,1,n
#define rep(x,y,z) for(int x=(y);x<=(z);x++)
#define per(x,y,z) for(int x=(y);x>=(z);x--)
#define repn(x) rep(x,1,n)
#define repm(x) rep(x,1,m)
#define pb push_back
#define e(x) for(int i=h[x],y=to[i];i;i=nxt[i],y=to[i])
#define E(x) for(auto y:p[x])
#define Pi pair<int,int>
#define ui unsigned ll
inline int read(){int s=0,w=1;char c=getchar();while(c<48||c>57) {if(c=='-') w=-1;c=getchar();}while(c>=48&&c<=57)s=(s<<1)+(s<<3)+c-48,c=getchar();return s*w;}
inline void pf(int x){if(x<0) putchar('-'),x=-x;if(x>9)pf(x/10);putchar(x%10+48);}
using namespace std;
const int N =2e5+5,M=1e6+5,MM=N*2,inf=(1LL<<30)-1;
mt19937 rd(20080626);
int n,m,k,tot;
bool Tiao=1;
inline int idl(int x){
	return x;
}
inline int idr(int x){
	return x+tot; 
}
struct node{
	int x,y,id,ty;
}a[N<<1];
map<Pi,int>P;
int nxt[N<<1],pre[N<<1],Mx,root[N<<1];
struct seg{
	int mx,id;
}xd[N];
inline void getup(int x){
	xd[x]=xd[x<<1].mx>=xd[x<<1|1].mx?xd[x<<1]:xd[x<<1|1];
}
inline void modify(int x,int l,int r,int p,int k){
	if(l==r)return xd[x]={k,l},void();
	p<=mid?modify(lc,p,k):modify(rc,p,k),getup(x);
}
struct fhq{
	int l,r,key,siz,sm,p,k,mp,f,le,lp;
}t[MM];
int cnt;
inline void create(int id,int ty,int ex){
	a[id].ty>0?t[id+ty*tot]={0,0,(int)rd(),1,1,1,1,1,0,ex,ex}:t[id+ty*tot]={0,0,(int)rd(),1,0,inf,0,inf,0,ex,ex};
}
inline void Getup(int x){
	t[L(x)].f=t[R(x)].f=x;
	t[x].siz=t[L(x)].siz+t[R(x)].siz+1,t[x].sm=t[L(x)].sm+t[R(x)].sm+t[x].k;
	t[x].mp=min({t[L(x)].mp,t[L(x)].siz+t[x].p,t[L(x)].siz+1+t[R(x)].mp});
	t[x].le=min({t[L(x)].le,t[L(x)].siz+t[x].lp,t[L(x)].siz+1+t[R(x)].le});
} 
inline Pi split(int x,int k){
	if(!x)return {0,0};
	t[x].f=0;
	if(k<=t[L(x)].siz){
		Pi now=split(L(x),k);
		L(x)=now.second,Getup(x),t[now.first].f=0;
		return {now.first,x};
	}
	Pi now=split(R(x),k-t[L(x)].siz-1);
	R(x)=now.first,Getup(x),t[now.second].f=0;
	return {x,now.second};
} 
inline int merge(int x,int y){
	t[x].f=t[y].f=0;
	if(!x||!y)return x|y;
	if(t[x].key<t[y].key)return L(y)=merge(x,L(y)),Getup(y),y;
	return R(x)=merge(R(x),y),Getup(x),x;
}
inline int getrt(int x){
	int nw=x;
	while(t[nw].f)nw=t[nw].f;
	return nw;
}
inline int getps(int x){
	int ans=1+t[L(x)].siz;
	while(t[x].f){
		if(x==R(t[x].f))ans+=t[L(t[x].f)].siz+1;
		x=t[x].f;
	}
	return ans;
}
int st[MM],tp;
map<int,int>Q[20005];
bool v[MM];
inline int getid(int x){
	return !Q[x].size()?0:(*Q[x].begin()).second;
}
inline void build(int s){
	tp=0;
	while(s)st[++tp]=s,s=nxt[s];
	int rt=st[1],k=0,id=0;
	rep(i,2,tp)rt=merge(rt,st[i]);
	rep(i,1,tp)if(v[st[i]])return modify(Root,a[st[i]].y,tp-i+1),void();
}
inline int getr(int x){
	while(R(x))x=R(x);
	return x;
}
inline int getl(int x){
	while(L(x))x=L(x);
	return x;
}
inline int got(int rt){
	if(!rt)return rt;
	int fir=t[rt].mp;
	if(fir>t[rt].siz)return rt;
	Pi now=split(rt,fir); 
	st[++tp]=getr(now.first);
	if(st[tp]>tot)st[tp]-=tot;
	return merge(now.first,got(now.second));
}
inline void del(int rt){
	if(!rt)return;
	int x=t[rt].le;
	if(x>t[rt].siz)return;
	Pi now=split(rt,x);
	modify(Root,a[getr(now.first)].y,0),merge(now.first,now.second);
}
inline void ins(int rt){
	if(!rt)return;
	int x=t[rt].le;
	if(x>t[rt].siz)return;
	Pi now=split(rt,x-1);
	int y=getl(now.second);
	if(y>tot)y-=tot;
	modify(Root,a[y].y,t[now.second].sm),merge(now.first,now.second);
}
inline void Clear(int x,int rt){
	int ps=getps(x);
	Pi A=split(rt,ps-1),B=split(A.second,1);
	t[x].k=t[x].sm=0,t[x].le=t[x].lp=t[x].mp=t[x].p=inf;
	merge(A.first,merge(B.first,B.second));
}
inline void Update(int x){
	if(!x)return;
	int rt=getrt(x),ps=getps(x);
	del(rt);
	Pi A=split(rt,ps-1),B=split(A.second,1);
	t[x].k=t[x].sm=t[x].le=t[x].lp=t[x].mp=t[x].p=1,merge(A.first,merge(B.first,B.second));
}
inline void Delete(int x){
	int pid=getid(a[x].y),nid; 
	v[x]=v[x+tot]=0,Q[a[x].y].erase(a[x].x),nid=getid(a[x].y);
	if(a[x].y<=n/2&&nid)nid+=tot;
	int rtl=getrt(x),rtr=getrt(x+tot);
	del(rtl),del(rtr),Clear(x,rtl),Clear(x+tot,rtr);
	if(pid==x)Update(nid);
	if(a[x].y!=1&&a[x].y!=n){
		int psl=getps(x),psr=getps(x+tot);
		Pi A=split(rtl,psl-1),B=split(rtr,psr-1);
		rtl=merge(A.first,B.second),rtr=merge(B.first,A.second);
	}
	ins(rtl),ins(rtr);
	if(pid==x){
		if(nid)ins(getrt(nid));
	}
}
inline void solve(int s){
	if(a[s].y<=n/2)s+=tot;
	tp=0;
	int rt=getrt(s),ps=getps(s);
	Pi now=split(rt,ps-1);
	now.second=got(now.second),rt=merge(now.first,now.second);
	rep(i,1,tp){
		int x=st[i];
		a[x].ty--;
		if(!a[x].ty)Delete(x);
	}
}
vector<int>p[N]; 
inline bool cmp(int x,int y){
	if(x>tot)x-=tot;if(y>tot)y-=tot;
	return a[x].x<a[y].x;
}
signed main(){
	n=read(),m=read(),k=read(),t[0].p=t[0].mp=t[0].le=t[0].lp=inf; 
	repm(i){
		int x=read(),y=read();
		P[{x,y}]++,Mx=max(Mx,x);
	}
	repm(i)modify(Root,i,0);
	for(auto y:P)tot++,a[tot]={y.first.first,y.first.second,tot,y.second},Q[a[tot].y][a[tot].x]=tot;
	repn(i){
		int id=getid(i);
		if(!id)continue;
		if(i<=n/2)v[idr(id)]=1;
		else v[idl(id)]=1;
	}
	rep(i,1,tot){
		if(a[i].y!=1)p[(a[i].x+a[i].y-1)%(n*2-2)].pb(i);
		if(a[i].y!=n)p[((a[i].x-a[i].y+1)%(n*2-2)+n*2-2)%(n*2-2)].pb(i+tot);
	}
	rep(i,1,tot)a[i+tot]=a[i];
	rep(i,0,n*2-3){
		sort(p[i].begin(),p[i].end(),cmp);
		int siz=p[i].size();
		rep(j,0,siz-2){
			int y=p[i][j+1];
			if(a[p[i][j+1]].y!=1&&a[p[i][j+1]].y!=n)y+=y<=tot?tot:-tot;
			nxt[p[i][j]]=y,pre[y]=p[i][j];
		}
	}
	rep(i,1,tot)create(i,0,v[i]?1:inf),create(i,1,v[i+tot]?1:inf);
	rep(i,1,tot*2)if(!pre[i])build(i);
	int sum=0;
	while(k--){
		printf("%d %d\n",xd[1].id,xd[1].mx);
		sum+=xd[1].mx;
		if(xd[1].mx>=1)solve(getid(xd[1].id));
	}
	cout<<sum;
	return 0;
}