【C++】二叉搜索树

1. 二叉搜索树的概念

二叉搜索树又叫二叉排序树，它或者是一颗空树，或者是具有以下性质的二叉树：

• 若它的左子树不为空，则左子树上的所有结点都小于根节点上的值
• 若它的右子树不为空，则右子树上的所有结点都大于根节点上的值
• 它的左右子树也分别是二叉搜索树

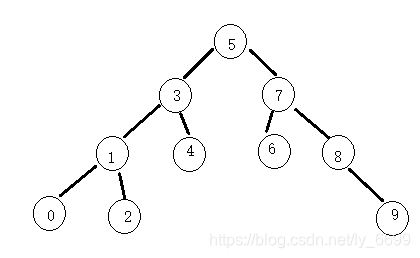
例：int a [ ]={5，3，4，1，7，8，2，6，0，9}构成的二叉搜索树如下：

二叉搜索树的特点：中序遍历后会得到一个升序排列的数组。

2. 二叉搜索树的操作

2.1 查找 key

其中：右树的值 > 根节点的值 > 左树的值
若根节点不为空：
若根节点的值value==key 则返回当前节点
若根节点的值value > key 则在其左树继续查找
若根节点的值value < key 则在其右树继续查找
否则返回空值 nullptr

Node* Find(const K& value)//查找一个元素，时间复杂度为O(logN)
		{
   
   
			Node* cur = _root;
			while (cur)
			{
   
   
				if (value > cur->_val)
					cur = cur->_right;
				else if (value < cur->_val)
					cur = cur->_left;
				else
					return cur;   //找到返回当前结点
			}
			return nullptr;      //找不到返回空值
		}

2.2 插入

若树为空则直接插入
若树不为空，则按二叉搜索树的性质确定插入位置，再进行插入
插入成功返回true，插入失败（插入相同的值）返回false

bool Insert(const K& value)//插入一个元素
		{
   
   
			if (_root == nullptr)//若树为空时，可