Arrangement of lines

1. 定义：A(L)是由顶点/边/面组成的细分平面

2. max vertices=n(n-1)/2

max edges = n^2

 

增量算法：

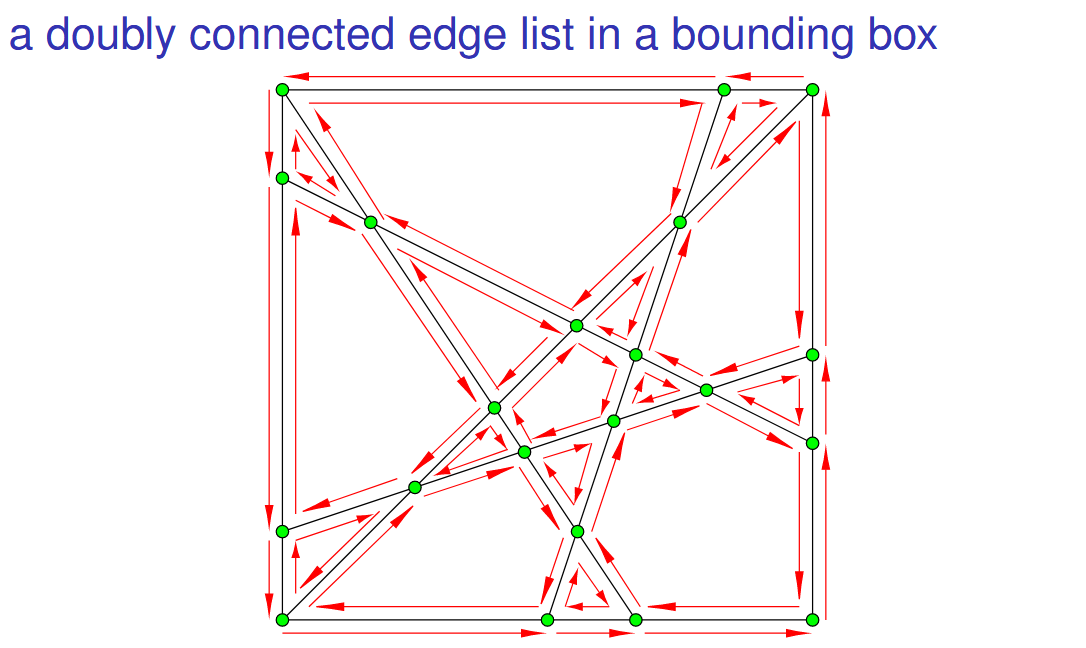
①计算交点，时间复杂度O()

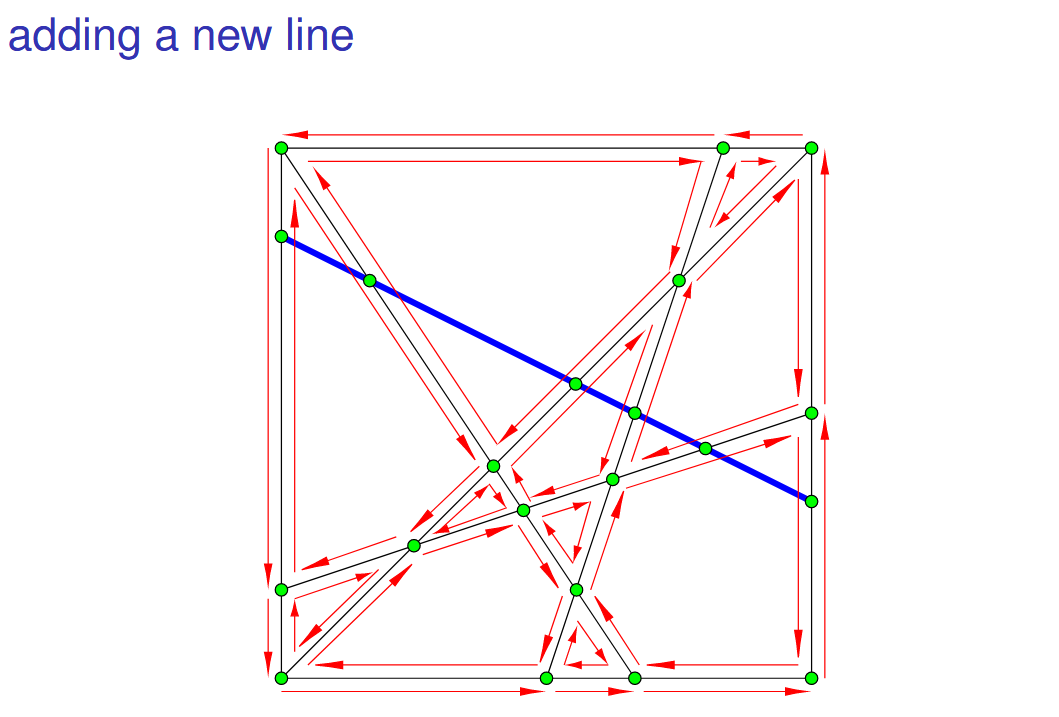
②添加新线

延新线从左到右走，通过边e 进入face，next指针指向出边e'

找到e'的邻接面，继续....

如果从existing vertex v离开，寻找v附近的面直到找到l穿过的下一个面

总步骤：

Exercise：

Consider the face f where the new line leaves through a vertex. Describe the finding of the face adjacent to f.

查找包含当前vertex的face，判断该face和li是否会相交。