前缀异或和与位运算

前缀异或和与位运算的算法解析

原创已于 2025-08-12 15:50:01 修改 · 1.2k 阅读

17 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #前缀异或+位运算 #蓝桥杯

于 2025-08-12 15:49:20 首次发布

算法同时被 2 个专栏收录

5 篇文章

订阅专栏

蓝桥杯题集

4 篇文章

订阅专栏

前言：相信学习算法的人都听说过前缀和，但是前缀异或和也是算法题所常考的内容，并且前缀异或和常常与位运算联系在一起，下面我来细讲一下这两个知识的原理，让大家真正搞懂该知识点。

2.1比如：有一个数组：1 2 3 4 5 6 求从3到5的子段异或和

一、关于异或和前缀异或和

1.异或的运算：

二进制位运算，如果两个数字的二进制位在该位相同，则运算结果为0，如果两个数字的二进制位在该位是不同的，那么运算结果为1.

1.1比如：计算2^3:

2的二进制： 1 0

3的二进制： 1 1

2^3的二进制位：0 1

所以2^3=1

所以可以将异或的运算看成为：二进制下的不进位加法

2.子段异或和

2.1比如：有一个数组：1 2 3 4 5 6 求从3到5的子段异或和

常规方法：从3到5遍历一遍，得到异或和，但是时间复杂度大：O(n)

所以引入前缀异或和可以将O(n)的时间复杂度提高到O(1)

2.2前缀异或和

2.2.1异或运算的小结论：

1. A^A=0;//两个相同的数异或在一起结果为零

2. 任意两个数异或都可以得到另外一个数

A^B=C

B^C=A

C^A=B

2.2.2前缀和和前缀异或和

数组a： 1 2 3 4 5

前缀和数组s：1 3 6 10 15 s[i]=s[i-1]+a[i]

前缀异或和s：s[i]=s[i-1]^a[i]

2.3优化：

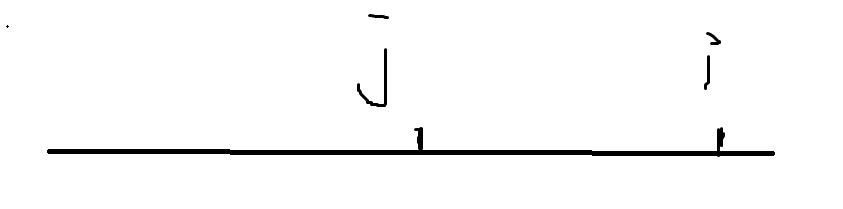假设：要求j--i这一段区间的异或和：公式：sum[i,j]=s[i]^s[j-1]

证明：因为：s[i]=s[j-1]^sum[j,i] 用到 异或运算的小结论：任意两个数异或都等于另外一个数

所以：可以通过预处理出前缀异或和数组，直接求出任意一段的前缀异或和

二、关于位运算

首先先拿一个蓝桥杯真题：P9236 [蓝桥杯 2023 省 A] 异或和之和 - 洛谷

[蓝桥杯 2023 省 A] 异或和之和

## 题目描述

给定一个数组，分别求其每个子段的异或和，并求出它们的和。或者说，对于每组满足 1≤L≤R≤n 的 L,R，，求出数组中第 L 至第 R 个元素的异或和。然后输出每组 L,R 得到的结果加起来的值。

输入格式

输入的第一行包含一个整数 n。

第二行包含 n个整数Ai，相邻整数之间使用一个空格分隔。

输出格式

输出一行包含一个整数表示答案。

输入输出样例

输入

```
5
1 2 3 4 5
```

输出：

```
39
```

对于 30% 的评测用例，n≤300；

对于 60% 的评测用例，n≤5000;

对于所有评测用例，1≤n≤105，0≤Ai≤220。

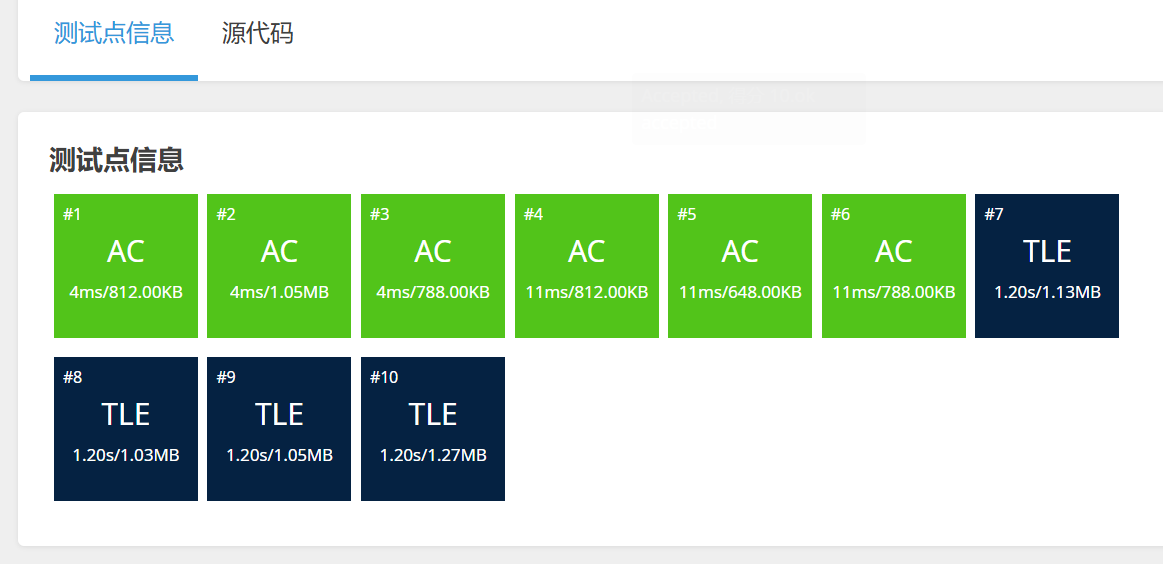
首先根据上面讲的前缀异或和的方法，我们可以用暴力解，得到60%的分数：暴力代码如下：

#include<iostream>

using namespace std;
const int N=1e5+10;
int n,arr[N],sum[N];
int main(void)
{
    cin>>n;
    for(int i=1;i<=n;i++)
    {
        cin>>arr[i];
        sum[i]=sum[i-1]^arr[i];
    }
    long long ans=0;
    for(int i=1;i<=n;i++)
    {
        for(int j=i;j<=n;j++)
        {
            ans+=(sum[i-1]^sum[j]);
        }
    }
    cout<<ans<<endl;
    return 0;
}

但是过不了全部的测试用例：

所以我们引入位运算的解法：（下面都是根据这个题来思考的）

2.1处理位运算常用方法：

2.1.1拆位法

将一个数拆成二进制位

假设将一段区间中的数字进行拆位之后进行异或：

00110101010

00101010101

10101011101

01010001010

11000001000

2.1.2贡献法

题目问的是区间异或和，但是从区间去考虑的话，时间复杂度会超，所以我们换一种思路，从每个元素对最终答案的贡献值去考虑。

所以：我们发现通过拆位只有1对结果会有贡献，当每一位的1的数目为偶数是结果为0，当每一位的1的数目为奇数时结果为1,

如果有贡献，贡献又是多少呢？---2^i

总结：当一个区间，这一位所对的1的个数是奇数时，这一位就产生了贡献，贡献为2^i(i表示第几位)，如果一个区间内，这一位所对的1的个数为偶数，这一位就不产生贡献

所以最优解决上面那道题的思路就很清晰了：

首先求前缀异或和数组
两层循环，一层枚举30个位，一层枚举前缀异或和数组
定义两个变量，c0和c1，记录遍历到的前缀异或和之后的每个数的第i位为0的个数和为1的个数
分两种情况：一种是遍历到的前缀异或和数组中的元素的第i位为1：用前面0的个数乘上2的i次方；一种是遍历到的前缀异或和数组中的元素的第i位为0：用前面1的个数乘上2的i次方

代码如下：

#include<iostream>

using namespace std;
const int N=1e5+10;
#define int long long
int n,arr[N];
signed main(void)
{
    cin>>n;
    for(int i=1;i<=n;i++)
    {
        cin>>arr[i];
        arr[i]=(arr[i]^arr[i-1]);
    }
    int ans=0;
    for(int i=0;i<=30;i++)
    {
        int c1=0,c0=1;
        for(int j=1;j<=n;j++)
        {
            if(((arr[j]>>i)&1)==1)
            {
                c1++;
                ans=ans+c0*(1<<i);
            }
            else 
            {
                c0++;
                ans=ans+c1*(1<<i);
            }
        }
    }
    cout<<ans<<endl;
    return 0;
}

如果想巩固这个算法推荐大家做一下这道题：

码蹄集

最后祝大家多多AC！！！！