一道小题带你入门dfs算法：递归实现指数型枚举

题目：从1--n这n个整数中随机选取了任意多个，输出所有可能的选举方案

输入格式：

输入一个整数n

输出格式：

每行输出一种方案

同一行内的数必须升序排列，相邻两个数用恰好1个空格隔开

对于没有选任何数的方案，输出空行。

数据范围：

1<=n<=15

输入样例：

3

输出样例：

3

2

2 3

1

1 3

1 2

1 2 3

一、分析这道小题

首先它考察的相当于高中的数学题--集合，比如当n=3时，就相当于求1--3的子集有几个各有多少，它也可以换一种问法：从1--n这n个整数中随机选取任意多个，输出所有可能的选择方案？我们都知道有2的n次方种  但是如何将每一个都输出出来这是一个大问题。

二、利用递归搜索树来辅助理解dfs的原理

我拿n=3为例子：搜索树如下：

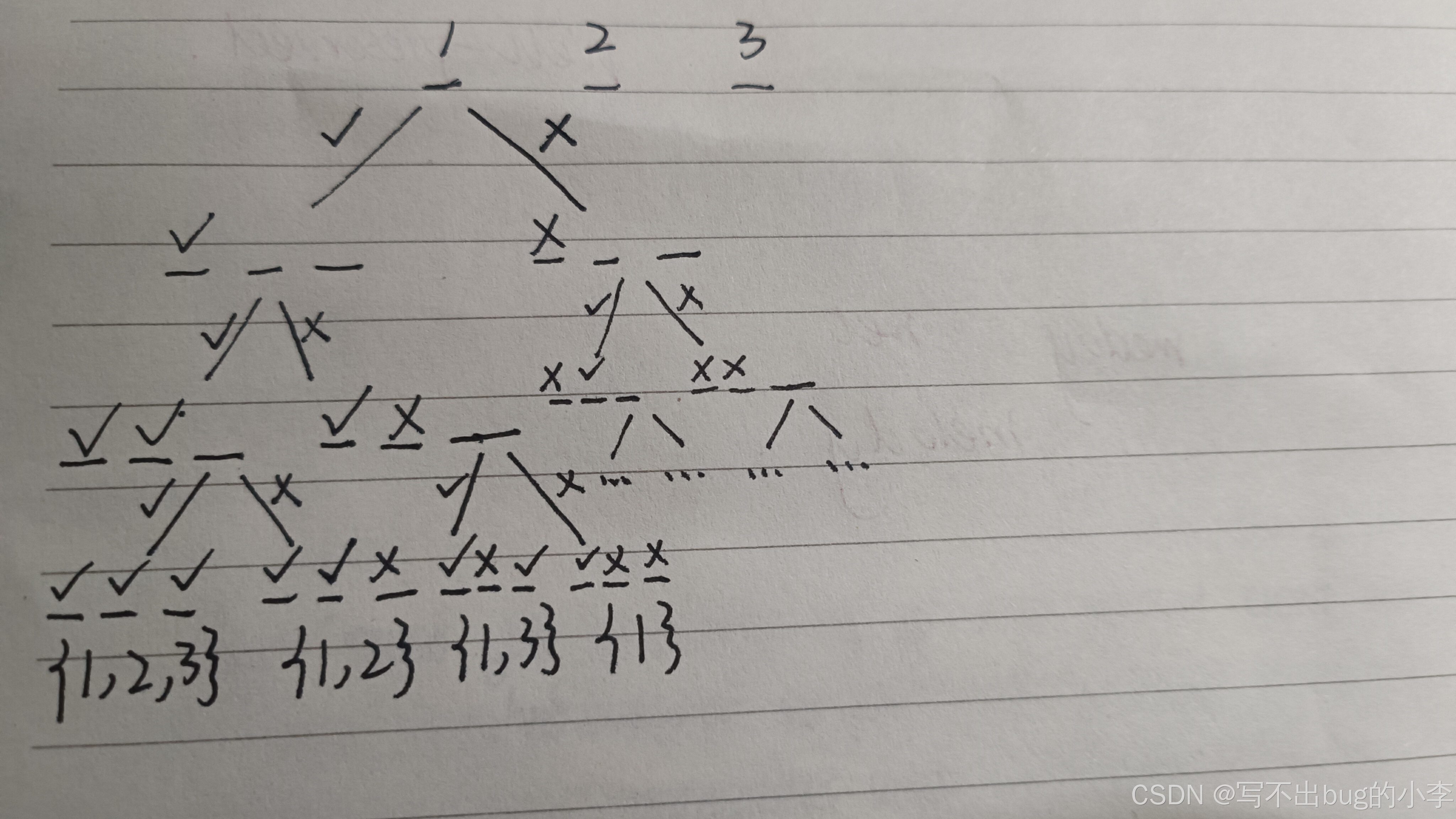
大家都应该知道：dfs算法是深度优先搜索

深度优先搜索的规则和过程就是：从图中的某个初始点v出发，首先访问初始点v，然后选择一个与顶点v相邻且没被访问过的顶点w，以w为初始顶点，再从它出发进行深度优先遍历，直到图中与顶点v邻接的所有顶点都被访问过为止，显然这个遍历过程是一个递归过程

三、代码实现

在用代码实现之前先搞明白我们怎么记录一个状态：一个数是选择还是不选还是待定

我们可以借助一个长度为n的数组来记录每个数是选还是不选

#include<iostream>
#include<algorithm>
#include<string>
using namespace std;
const int N = 25;
int n;
int state[N];//记录每个数的状态，0表示还没考虑，1表示选这个数，2表示不选这个数
void dfs(int x)//x表示当前枚举到了哪个位置
{
	if (x > n)
	{
		for (int i = 1; i <= n; i++)
		{
			if (state[i] == 1)
			{
				cout << i << " ";
			}
		}
		cout << endl;
		return;
	}
	//选
	state[x] = 1; 
	dfs(x + 1);
	state[x] = 0;//恢复现场

	//不选
	state[x] = 2;
	dfs(x + 1);
	state[x] = 0;
}
int main(void)
{
	cin >> n;
	dfs(1); 
	return 0;
}

运行结果你会发现：和答案的结果相反，留一个小问题你们可以思考一下：怎样修改运行结果才能和答案的顺序一样？？

解答：我们直接将选和不选的代码调换一下位置就可以了

总结：算法中我认为递归算是比较难理解的问题了，尤其是递归中的回溯问题，但是只要沉下心来，无论什么算法，一个小时不能解决的那我们就花费两个小时，一天解决不了的我们就花费一个星期，当理解之后就会发现我们的逻辑和思维又上升了一个阶段，关关难过关关过，事事难成事事成！！！共勉！！！