线段树 POJ2528

POJ：http://poj.org/problem?id=2528

这两天在学习线段树算法，参考了网上许多线段树的资料，用Google搜一下，就能搜到很多，这里就不详细解释什么事线段树了。

线段树在解决区间重合问题，比如求一段区间，最大值，最小值，求和等问题非常有效，一次查询的时间复杂度是log(n)，时间复杂度非常理想。

题目大意：在墙壁上贴广告，广告的版面有大有小，并且贴广告有先后之分，后面贴的广告会覆盖前面的广告，求解最后能看到的广告面，如下图所示：

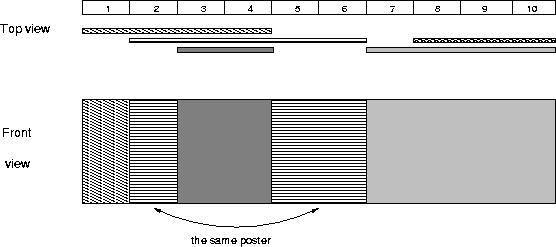
两种视图，最后从From View能看见的广告数目是4。

题目分析：这里面不仅用到了线段树，还用到了离散化方法，意思是将区间范围很大的数据集映射到较小的数据集，这样构造线段树更加高效，具体方法就是把所有线段的端点排序，从左至右，一次编号（两条线段相同的端点，用同一个编号），并且将新的编号替代原来的端点值，这样既不改变各个线段的性质，同时能够缩小数据范围。

具体代码如下：

/*
 * my_poj2528.cpp
 *
 *  Created on: 2012-6-15
 *      Author: ict
 */

#include <cstring>
#include <cstdlib>
#include <cstdio>
#include <algorithm>
using namespace std;

#define MAX 20010

#define LC(x) ((x) << 1)	//计算左孩子位置
#define RC(x) (((x) << 1) + 1)	//计算右孩子位置

struct Node
{
	int l;	//线段左端点值
	int r;	//线段右端点
	int c;	//线段的颜色
}nodes[MAX * 5];

int map[MAX][2];	//记录输入线段的左右两个端点
int record[MAX];	//记录颜色是否已经出现
int total;

//用于离散化
struct Line
{
	int point;	//记录端点的坐标
	int num;	//记录原来的编号
}line[MAX * 2];

int mycmp(const Line &a, const Line &b)
{
	return a.point < b.point;
}

void buildTree(int l, int r, int position)
{
	nodes[position].l = l;
	nodes[position].r = r;
	nodes[position].c = 0;	//初始化颜色都为0
	if(l == r)
		return ;

	int mid = (l + r) >> 1;
	buildTree(l, mid, LC(position));	//构造左子树
	buildTree(mid + 1, r, RC(position));	//构造右子树

	return ;
}
/*
 * @para l, r: 线段的左、右端点
 * @para position: 插入树的位置
 * @para color: 线段的颜色
 */

void insert(int l, int r, int position, int color)
{
	if(nodes[position].l == l && nodes[position].r == r)	//刚好覆盖，修改颜色，直接返回
	{
		nodes[position].c = color;
		return ;
	}

	if(nodes[position].c > 0)	//如果当前线段已经有颜色，先将颜色复制给左右两个子树，非常重要
	{
		nodes[LC(position)].c = nodes[position].c;
		nodes[RC(position)].c = nodes[position].c;
		nodes[position].c = 0;	//标记线段没有颜色
	}

	if(l >= nodes[RC(position)].l)	//完全在右子树
		insert(l, r, RC(position), color);
	else
		if(r <= nodes[LC(position)].r)	//完全在左子树
			insert(l, r, LC(position), color);
		else		//两个子树都有
		{
			insert(l, nodes[LC(position)].r, LC(position), color);
			insert(nodes[RC(position)].l, r, RC(position), color);
		}
}

/*
 * @para position: 查询指定线段的颜色
 */
void update(int position)
{
	if(nodes[position].c != 0)	//如果当前线段有颜色，记录，并且直接返回
	{
		if(!record[nodes[position].c])
		{
			total++;
			record[nodes[position].c] = 1;
		}
		return ;
	}
	//如果当前线段没有颜色，递归调用左右子树，查询颜色
	update(LC(position));
	update(RC(position));
	return ;
}

int main()
{
	int number;
	int n;
	int i;
	scanf("%d", &number);
	while(number--)
	{
		scanf("%d", &n);

		for(i = 0; i < n; i++)
		{
			scanf("%d%d", &map[i][0], &map[i][1]);
			line[2*i].point = map[i][0];	//记录数据，用于离散化
			line[2*i + 1].point = map[i][1];
			line[2*i].num = -(i + 1);	//线段第一个端点用负数记录
			line[2*i + 1].num = i + 1;	//线段第二个端点用正数记录
		}

		//首先将所有端点排序
		sort(line, line + 2*n, mycmp);
		int temp = line[0].point;
		int count = 1;	//重新开始编号，从1开始
		for(i = 0; i < 2*n; i++)
		{
			if(temp != line[i].point)	//如果当前端点和前面的端点不一样，编号值+1
			{
				count++;
				temp = line[i].point;
			}

			if(line[i].num < 0)
				map[-line[i].num - 1][0] = count;
			else
				map[line[i].num - 1][1] = count;
		}

		buildTree(1, count, 1);

		for(i = 0; i < n; i++)
			insert(map[i][0], map[i][1], 1, i + 1);

		memset(record, 0, sizeof(record));
		total = 0;
		update(1);
		printf("%d\n", total);
	}

	return 0;
}