本文介绍了使用分治策略解决最大子段和问题的伪代码描述，通过将数组二分并计算左右及跨边界的最大和，递归确定最大子段和的位置。时间复杂度分析表明该方法为O(N)，其中N为数组长度。分治法在处理大型问题时展现出高效和独立性，但空间需求较大。
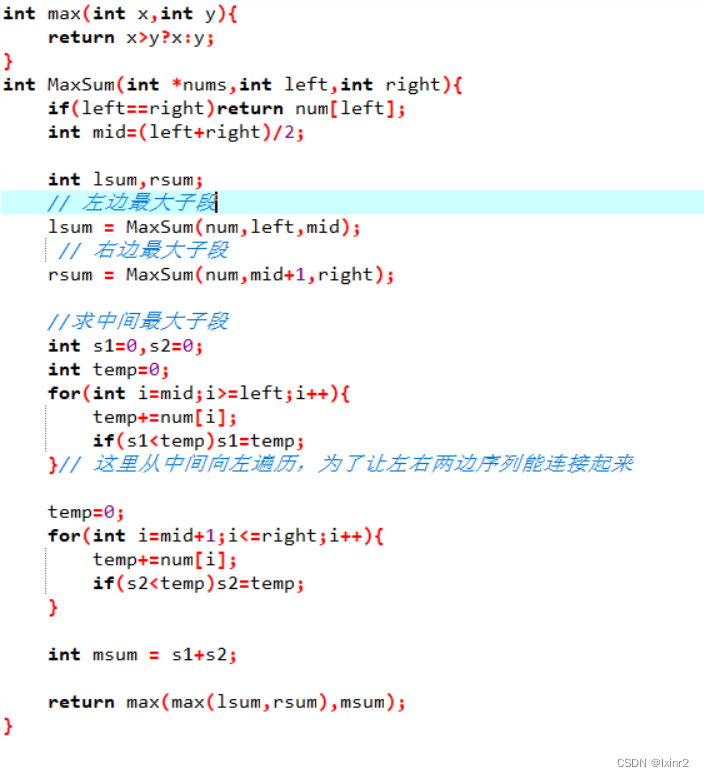
一、以伪代码描述最大字段和的分治算法
所谓分治法，就是将大问题划分为多个小问题进而更容易解决，最后将多个小问题凑在一起就将大问题解决了。所以在这里也要将大型数组二分，同时就需要面临，最大子段和的位置问题：
在最左边数组中
在正中间，包含两数组
在最右边数组中
所以只需要将两边数组的和求出，以及整体的和进行相互对比就可以知道最大子段和所在的位置。进而不断递归就可以求出具体位置了。
二、分析时间复杂度
在（left+right）/2处，把大问题分成了两个部分的小问题
在跨边界求和的时候，我们需要计算 从center出发的到 left方向的最大和，每次增加一个元素，通过比较，得到最大的和，时间复杂度为O（N）
同样， 从center+1 出发的到 right 方向的最大和，每次增加一个元素，通过比较，得到最大的和，时间复杂度 为 O(N) 。所以，时间复杂度为 O(N)
三、对分治法的体会和思考
分治法对于大型问题的解决，提供了一种可靠且快速的思维方式。并且同级各小部分之间是互相独立的，所以不会出现牵一发而动全身的情况。因为相同元素的顺序不会颠倒，是稳定排序。只是分治法需要的空间复杂度相对要求较大，需要数组的辅助。
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
