生成模型初探：从PCA到AE

最新推荐文章于 2023-02-19 10:06:46 发布

corgi_xx

最新推荐文章于 2023-02-19 10:06:46 发布

阅读量717

点赞数 1

分类专栏： ML python 文章标签： machine learning PCA generative model

本文链接：https://blog.youkuaiyun.com/lxhdy12345/article/details/102679980

版权

python 同时被 2 个专栏收录

4 篇文章

订阅专栏

2 篇文章

订阅专栏

生成模型初探：从PCA到AE

人类较机器蕴含智能，其中最重要的是一种创造性。无论是作诗绘画还是音乐，艺术家都得在一定规则的限定下带着脚镣舞蹈，但是他们却可以跳出少数几个机械的规则，创造出无穷无尽的作品，这便是机械难以做到的事情。传统的机械学习，仅仅从数据库中检索答案似乎与创造新信息相去甚远；后来的统计学习，将随机性引入，但是面对庞大的参数空间却无能为力。直到神经网络的出现，才初步解决了这个问题，基于神经网络强大的非线性拟合能力可以对输入数据分布进行学习，只要对学习到的分布进行采样，就可以生成新的数据，这就是生成模型的基本形式。但是将随机性与采样引入深度学习还有很多其他的问题（比如采样这个操作是不可导的），对这些问题的研究衍生了现在很多生成模型，比如VAE、GAN、pixelCNN等等，这些将在后续的文章进一步补充，本文作为生成模型的初探，主要将顺着传统机器学习的轨迹，去解构“生成与创造”智能的本质。

PCA

乍看上去，PCA 是传统的数据挖掘手段，好像与生成模型这种“先进”概念相去甚远。而本文要说的是PCA做的不仅仅是降维，更是自编码器一个基本的雏形，其意义不仅在于压缩参数，更在通过压缩后的参数重现原始信息。

PCA(principal component analysis)，主成分分析法，是KL变换在协方差矩阵下的引申，KL变换是最优的正交变换，PCA也是这样一个正交变换。正如线性代数中的施密特正交化方法，将一个矩阵做正交变换是很有必要的，因为变换之后的矩阵在新的空间中可以由正交基分解，而每个正交基之间有最小的相关性：因为它们两两垂直。因此，PCA的目的是降低离散随机变量的相关性，使得数据在一个正交变换之后的新空间中具有最小的相关性，这样独立成分就可以被最大化分离，这是直观定性理解。

考虑这样一个数据集 $X$_{n*m}$$ （有m个样本，每一个样本有n个属性，组成一个n维度列向量），我们假设样本矩阵X已经归一化了（X的协方差矩阵和自相关矩阵相同）。我们的操作就是想通过一个正交变换矩阵 $D$_{n*l}$$ 将一个l维度的向量c变换回x而且要求变换回的x具有真实数据的最多的信息。显然这是一个最优化问题：

$$ \mathop{argmin}\limits_{\textbf{D}} $\left \| \textbf{X}-\textbf{D}\textbf{D}$^{T}$ \textbf{X}||\right \|$^{2}$,s.t.\textbf{D}^{T}\textbf{D}=\textbf{I}$

为了要求c变换回的x具有最大的信息保留我们还必须有：

$\textbf{c}$^{*}$=$ \mathop{argmin}\limits_{\textbf{c}} $\left \| \textbf{x}-\textbf{Dc}\right \|$^{2}$ \quad for \quad \textbf{x} \quad in \quad \textbf{X}$

在这个最优化问题中对c求导可以得到满足最大信息的c满足 $\textbf{c}=\textbf{D}^T\textbf{x}$ ，将这个代入第一个最优化问题有：

$$ \mathop{argmin}\limits_{\textbf{D}} $\left \| \textbf{X}-\textbf{D}\textbf{D}$^{T}$ \textbf{X}||\right \|$^{2}$,s.t.\textbf{D}^{T}\textbf{D}=\textbf{I}\\ =$\mathop{argmin}\limits_{\textbf{D}}$\,tr(\textbf{D}^T\textbf{XX}^T\textbf{D})$

这个是个二次型最大值的求解，显然，二次型最大值与 $\textbf{XX}^T$ 的特征值的最大值息息相关。而D也应该是 $\textbf{XX}^T$ 特征值对应的特征向量组成的矩阵，其中特征值越大，D作为分解的正交基占的比重越大。而那些小的特征值对于原始矩阵X信息贡献最小，完全可以忽略，这样就达到了降维的目的。具体的操作是对归一化的数据矩阵X求其协方差矩阵 $\textbf{XX}^T$ ，然后对其做特征分解并将特征值排序，得到D，只要取前l个最大的，就可以降维到c了。

具体的代码如下：

# -*- coding: utf-8 -*-
"""
Created on Thu Oct 17 21:32:37 2019

@author: lenovo
"""

import matplotlib.pyplot as plt # plt 用于显示图片
import matplotlib.image as mpimg # mpimg 用于读取图片
import numpy as np

imag = mpimg.imread('1.jpg') 
#将rbg转换为灰度图
def rgb2gray(rgb):
  return np.dot(rgb[...,:3], [0.299, 0.587, 0.114])
gray = rgb2gray(imag)
plt.subplot(211)
plt.imshow(imag) # 显示图片
plt.axis('off') # 不显示坐标轴
plt.show()
plt.subplot(212)
plt.imshow(gray,cmap='Greys_r') # 显示图片
plt.axis('off') # 不显示坐标轴
plt.title('original image')
plt.show()

'''
PCA 
图片是1200*1920的，可以看作是1920个1200维的数据
'''
#归一化：
N = 10 #降维的目标维度数目100
mean = np.mean(gray,axis = -1)
norm_gray = gray - mean.reshape([1200,1])
cov = np.dot(norm_gray,norm_gray.T)      #求出协方差矩阵，维度是1200*1200，相当于每一个维度互相的关系
e_vals,e_vecs = np.linalg.eig(cov)       #对协方差矩阵进行特征分解，得到特征值与特征向量

D = e_vecs[:,:N]                         #由于特征值已经排列好大小了，取其中最大的N个对应的特征向量组成D

encoded = np.dot(D.T,norm_gray)          #数据降维
print('降维后的维度：',encoded.shape)

decoded = np.dot(D,encoded)               #数据重建                                      

plt.figure(2)
plt.imshow(decoded,cmap ='Greys_r')
plt.title('encode in 10 dim')

#%%
#下面是不同的降维维度对应的恢复效果
plt.figure(3)
N = [5,10,15,20]
for i in range(4):
    D = e_vecs[:,:N[i]]
    encoded = np.dot(D.T,norm_gray)  
    decoded = np.dot(D,encoded)   
    plt.subplot(2,2,i+1)
    plt.imshow(decoded,cmap ='Greys_r')
    plt.title('_{}_dim'.format(N[i]))

下图是一个对新垣结衣图片压缩的演示，我们把图片看作X矩阵，就可以进行PCA降维，图中给了不同压缩维度l的压缩复原效果：

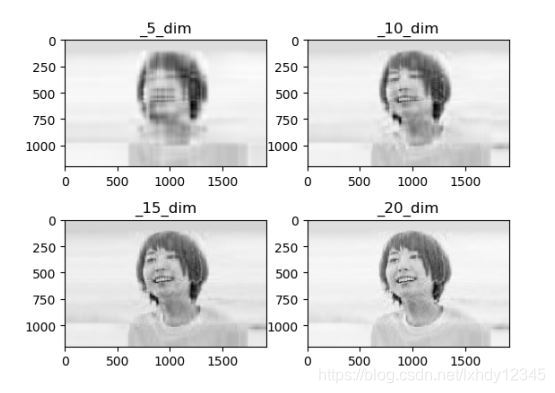
可以发现，在降维至5，基本就是人鬼模辩状态，随着l上升，可以看到更多的细节，当l=n，就可以完美复原，这个时候c也就成了完备编码。当然实际的图像压缩肯定不能用PCA，因为PCA对不同的数据压缩都要求不同的变换矩阵D，而且在传输时，也必须吧码表D传输，所以实际的音频或是图像的压缩常采用的是DCT（离散余弦变换），它是固定变换矩阵的，而且一定条件下是KL变换的最好近似。此外大规模求解特征值是一件极其消耗计算资源的事情，特别是在维度很高的情况下，一般对于高维数据，PCA的求解是通过奇异值分解（SVD），比如在sklearn库中就可以快速进行PCA,一般这种标准库中的PCA求解特征值是以求解奇异值来快速计算的。

将一幅图分解，然后复原好像有点模糊的图，好像除了能让存储空间小一点就没啥用了，这又与我们所述的创造性与人工智能有什么关系？我们再仔细观察这几个图片，当l=5时就是选取了前5个最大的特征值，而这个时候人脸的基本轮廓就初步有了，而后面的10、20乃至更高维，就是在这个基础上修修补补一些细节而已。这时候我们已经发现了一些压缩变量维度的规律，就是前几个变量代表图片中主要的轮廓，而后面的多数维度，都仅仅是一些细节。从信号处理的角度来说，就是前几维是图片信息的低频，而后面都是高频信息，说到低频高频，很多小朋友都会联想到一个著名的变换：傅里叶变换，而且巧合的是，离散傅里叶变换的矩阵也是正交的，它是一个正交变换，只不过在复数域上，叫做酉变换；更进一步，离散傅里叶变换的变换矩阵来自于数据的循环矩阵的特征值分解（这里请翻看具体的信号处理书籍），看来它也很类似PCA嘛。到这里，知道压缩后的维度对应轮廓还是细节、低频还是高频意味着什么呢？意味着，我们可以通过操纵这些维度，去控制生成的不同的图案。珊珊来迟，终于到了生成的时候。

我们想要生成新的图片，一般来说就是生成不同的轮廓以及不同的细节，但是多数人脸轮廓基本一致，而其细节千变万化，所以我们真正需要改变的就是那些后面的维度，而这些维度不但对应着细节，更多还对应着噪声（正是因为如此，忽略后面的维度可以降维而去除了噪声干扰），给不同的噪声好像就可以生成不同的细节？事实上，即使到现在类似VAE亦或是GAN的模型，其实也基本上实现的就是给不同噪声的操作，因为我们可以认为图案的细节就是分布被严格限制的噪声。当然要学习到这种噪声的分布需要拟合能力很强的神经网络。

当然，真实世界的多数数据没有像声音、图像这么有完备的解释，压缩出的维度既不对应低频也不对应高频，相互杂糅着，存在于我们这些小脑瓜难以想象的高维中。为了拟合复杂的分布，我们可以想到的方法就是用多次PCA，每次降维一小点，提取足够的信息再降维一小点，这就是AE（自编码器的雏形），实际上PCA就是只有一个隐层的线性自编码器，只要误差函数一致优化结果是等效的，只不过，自编码器由于激活函数的存在，被赋予了更多的非线性拟合能力，这也是PCA所难以企及的，也为其真正用于真实数据奠定基础。