第6章 向量处理机

向量处理机是有向量数据表示的处理机，分向量流水处理机和阵列处理机两类。

向量流水处理机是以时间重叠途径开发的，而阵列处理机是以资源重复途径开发的。

6.1 向量的流水处理与向量流水处理机

6.1.1 向量的处理和向量的流水处理

例：求向量D=Ax(B+C)

如果采用逐个求D向量元素的方法，即访存取a_i、b_i、c_i元素求得d_i，再取a_i+1、b_i+1、c_i+1元素求得d_i+1，这种处理方式称为横向（水平）处理方式。

横向（水平）处理方式：逐个求向量元素的方法，宜在标量处理机上用循环程序实现，但却难以使流水线连续流动。

纵向（垂直）处理方式：向量各个元素一起处理。先整体处理B+C，得到结果为向量K，再处理AxK，得到向量D。

分组纵横处理：若向量的长度太长，超出寄存器数，则可将向量分割成若干组，每组都可以装入寄存器中，这样，每一组内均按纵向方式处理，而组和组之间则采用软件方法编制循环程序的方式依次循环处理。

结论：向量横向处理是向量的处理方式，但不是向量的流水处理方式；而向量的纵向处理和分组纵横处理既是向量的处理方式，也是向量的流水处理方式。

• 向量内部各元素很少相关
• 一般执行同一个操作
• 容易发挥流水效能

向量数据表示+流水线=向量流水处理机

6.1.2 向量流水处理机的结构举例

CRAY-1

支持4种向量指令：

• 向量和向量计算
• 向量和标量计算
• 从主存里面取数据放入向量寄存器（访存 LOAD）
• 从向量寄存器写入主存 （STORE）

6.1.3 通过并行、链接提高性能

一般可采用让多个流水线功能部件并行，流水线链接，加快条件语句和稀疏矩阵处理，加快向量的归约操作等办法来提高向量流水处理的性能。

只要不出现Vi冲突和功能部件冲突，各个Vi和功能部件之间都能并行工作，大大加快了向量指令的处理。

Vi冲突：指的是并行工作的各向量指令的源向量或结果向量使用了相同的Vi。

V4 <- V1 + V2;
V5 <- V1 ∧ V3；

这两条向量指令的源向量之一都取自V1，但首元素和向量长度可能不同，难以同时由V1来提供。

功能部件冲突：指的是同一个功能部件被要求并行工作的多条向量指令所使用

V4 <- V2 * V2;
V5 <- V1 * V6；

两条指令都要用浮点乘功能部件，那就需要第一条向量指令执行完释放出功能部件之后，第二条向量指令才能开始执行。

链接：CRAY-1由机器自动检查每一条向量指令是否可以与它前一条向量指令链接。如果满足条件，则在前一条指令的第一个结果分量到达向量寄存器组病可以用作本条向量指令的源操作数时，立即启动本条指令工作而形成链。

【1510真题】求向量D=Ax(B+C)，向量元素为浮点数，各向量元素个数均为N，参照CRAY-1方式分解为3条向量指令。
①V3<-存储器：访存取A送入V3寄存器组；
②V2<-V0+V1: B+C->K;
③V4<-V2XV3: KxA->D当采用下列3种方式工作时，各需多少拍才能得到全部结果？
(1)①、②和③串行执行。
(2)①和②并行执行后，再执行③；
(3)采用链接技术。

☆CRAY-1特点：

*启动访存：1拍；
*访存：6拍；（从存储器取）；
*送入流水线：1拍；
*存入寄存器：1拍；
整数加：3拍；
*浮点加：6拍；
*浮点乘：7拍；
浮点迭代求倒数：14拍；
逻辑运算(和、或、异或）：2拍
位运算：4拍

答：

(1)如题，
①需要启动访存+访存+存V3到寄存器=1+6+1=8(拍)，之后每个分量在流水线中只需要1拍即可流出，所以总时间为8+n-1=n+7(拍)
②需要送浮加部件+浮点加+存V2到寄存器=1+6+1=8(拍)，之后每个分量在流水线中只需要1拍即可流出，所以总时间为8+n-1=n+7(拍)；
③需要送浮乘部件+浮点乘+存V4到寄存器=1+7+1=9(拍)，之后每个分量在流水线中只需要1拍即可流出，所以总时间为9+n-1=n+8(拍)；
所以串行执行，总拍数为n+7+n+7+n+8=3n+22(拍)。
(2)由于各个向量的元素个数一样，所以，①和②并行，启动访存与送浮加部件并行，访存和浮加并行，存V3和存V2并行，一共需要1+6+1=8(拍)，之后每个分量在流水线中只需要1拍即可流出，所以总时间为8+n-1=n+7(拍)；
之后再执行③，所以总时间为n+7+n+8=2n+15(拍)。
(3)采用链接技术，也就是①和②并行，再和③链接，也就是直接把①和②执行的结果送入流水线，和③一起构成流水线，根据(2)中分析，①和②并行，需要1+6+1=8(拍)，然后③需要送浮乘部件+浮点乘+存V4到寄存器=1+7+1=9(拍),总的需要8+9=17(拍)，之后每个分量在流水线中只需要1拍即可流出，所以总时间为17+n-1=n+16(拍)；

6.2 阵列处理机的原理

6.2.1 阵列处理机的构型和特点

1. 阵列处理机的构型

阵列处理机有两种构型，差别主要在于存储器的组成方式和互联网络的作用不同。

构型1 分布式存储器阵列处理机

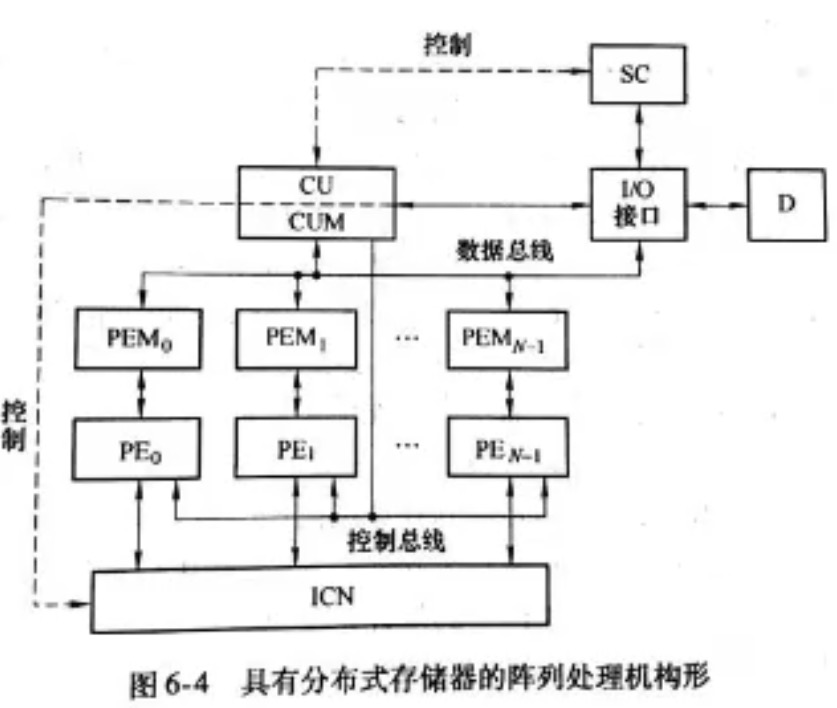
各处理单元（PE）有局部存储器（PEM）存放被分布的数据，只能被本处理单元直接访问。

PE之间通过互连网络（ICN）来交换数据。

所有PE由控制部件（CU）控制。

控制部件链接到管理处理机（SC）上。

管理处理机是一种通用机，用于管理系统资源，完成系统维护、输入/输出、用户程序的汇编及向量化编译、作业调度、存储分配、设备管理、文件管理等操作的功能。因此，处理单元阵列、互联网络和控制部件在内的阵列处理部分，可以看成了系统的后端处理机。

构型2 集中式共享存储器阵列处理机

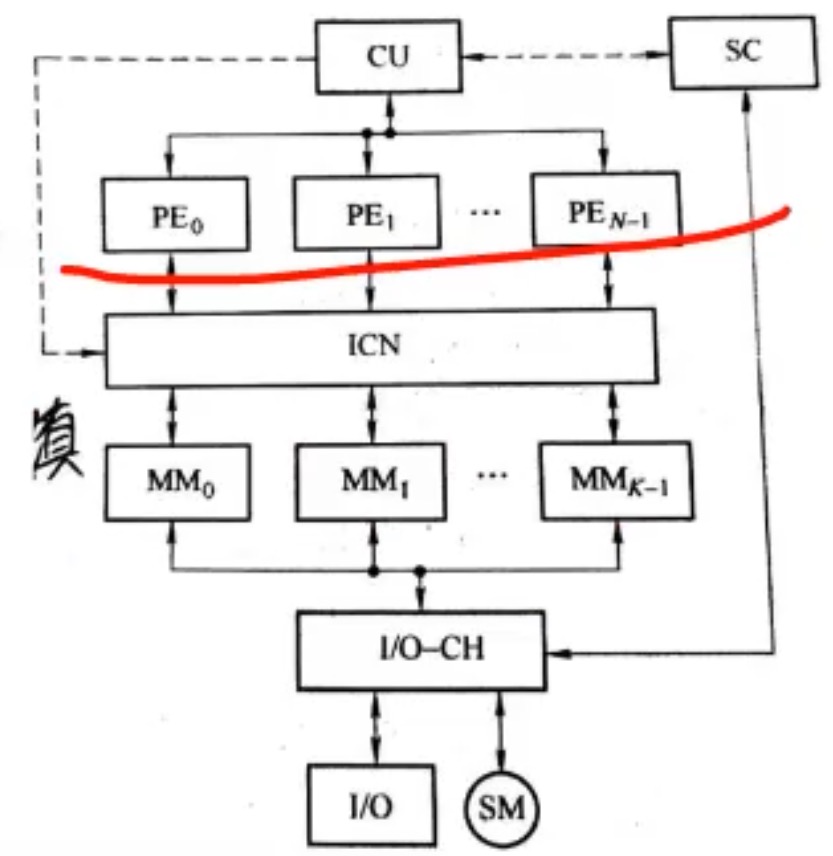
系统存储器由K个存储分体（MM₀ – MM_k-1)集中组成，经ICN为全部N个处理单元（PE₀ – PE_n-1)所共享。K >= N

2.阵列处理机的特点

• 1. 基于有限差分、矩阵、信号处理、线性规划等问题为背景，这些问题的共通特点是可以通过各种途径把它们转化为对数组或向量的处理
• 2. 单指令流多数据流处理 SIMD
• 3. 资源重复，而不是时间重叠
• 4. 利用并行性中的同时性，而不是并发性
• 5. 并行处理机主要是靠增大处理单元个数来提高运行速度，比起向量流水线处理机主要依靠缩短时钟周期来说，速度提高的潜力要大得多

阵列处理机实质上是由专门应对数组运算的处理单元阵列组成的处理机、专门从事处理单元阵列的控制及标量处理的处理机和专门从事系统输入/输出及操作系统管理的处理机组成的一个异构型多处理机系统。

6.2.2 ILLIAC Ⅳ的处理单元阵列结构

采用这种构型的阵列处理机是SIMD。

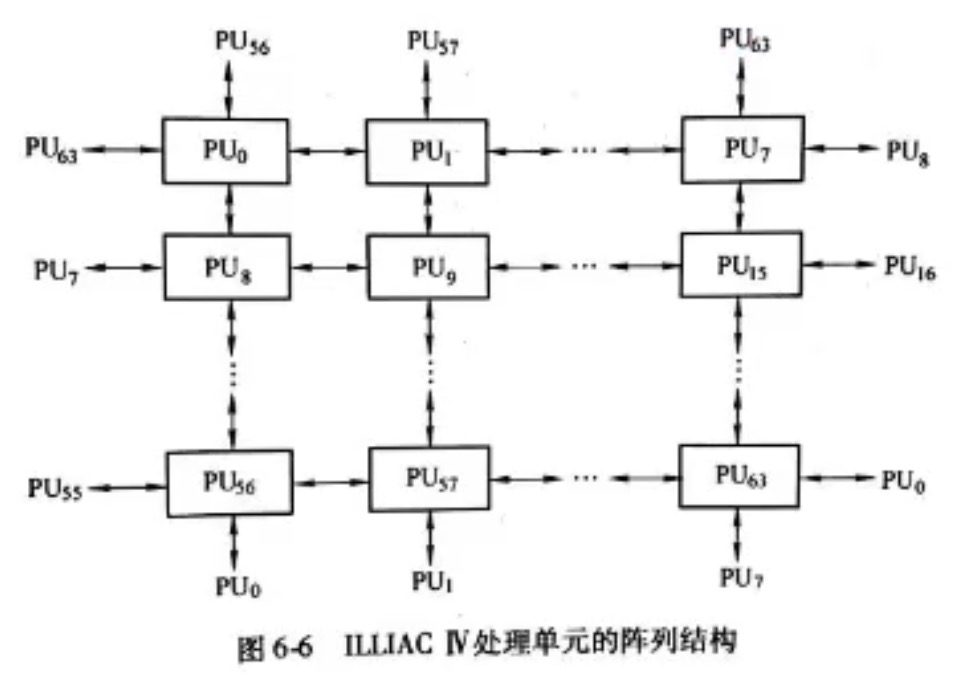
6.2.3 ILLIAC Ⅳ的并行算法举例

1.矩阵加

阵列处理机解决矩阵加是最简单的一维情况。

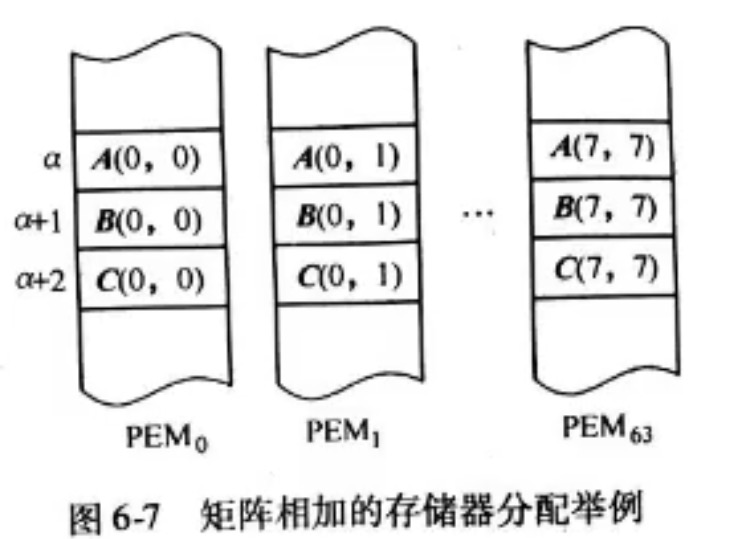
2.矩阵乘

矩阵乘是二维数组运算，比矩阵加要复杂。设A、B和C为3个8x8的二维矩阵，给定A和B，计算C=AxB的64个分量可用公式：

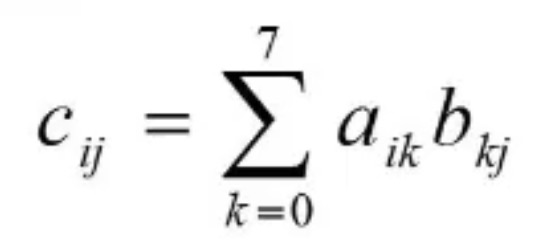
其中，0≤i≤7且0≤j≤7。

3.累加和

这是一个将N个数的顺序相加转为并行相加的问题。为得到各项累加的部分和与最后的总和，要用到处理单元中的活跃标志位。只有处于活跃状态的处理单元才能执行相应的操作。为叙述方便，取N=8，即有8个数A(I)顺序累加，其中0≤I≤7。
在SISD计算机上可以编写下列FORTRAN程序：
  C=0
  DO 10 I=0,7
10 C=C+A(I)

这是串行程序，需要8次加法时间，阵列处理机上，加这8次给两两细分到各个处理单元上处理，所以只需要log₂8=3次加时间即可。

6.3 SIMD计算机的互连网络

6.3.1 互连网络的设计目标与互连函数

在SIMD计算机中，无论是处理单元之间，还是处理单元与存储分体之间，都要通过互连网络进行信息交换。

SIMD系统的互连网络的设计目标是：

• 结构不要过分复杂，以降低成本；
• 互联要灵活，以满足算法和应用的需要；
• 处理单元间信息交换所需的传送步数要尽可能少，以提高速度性能；
• 能用规整单一的基本构件组合而成，或者经多次通过或者经多级连接来实现复杂的互连，使模块性好，以便于用VLSI实现并满足系统的可扩充性

简单背诵版

• 不过分复杂，以降低成本
• 灵活，以满足算法和应用的需要；
• 传送步数越少越好；
• 用基本构件组合而成，支持多级扩展

互连函数

互连函数表示互联网络的出端号和入端号的一一对应关系。

所有入端x和出端f(x)都用二进制编码，从两者的二进制编码上找出其函数规律。

6.3.2 互连网络应抉择的几个问题

操作方式有同步、异步及同步与异步组合3种。阵列处理机采用同步，多处理机采用异步或组合操作方式。

控制策略有集中和分布两种，多数现有的SIMD互连网络采用由集中控制部件对全部开关单元执行集中控制的策略。

交换方法有线路交换、包交换、线路与包交换3种。SIMD互连网络多采用硬连的线路交换，包交换多用于多处理机和计算机网络中。

网络拓扑结构有静态和动态两种，本书只讨论动态网络。

动态网络有单级和多级两类。动态单级网络只有有限的几种连接，必须经循环多次通过，才能实现任意两个处理单元之间的信息传送，故称动态单级网络为循环网络。动态多级网络是由多个单级网络串联组成的，以实现任意两个处理单元之间的连接。将多级互连网络循环使用，可实现复杂的互连，称循环多级网络或多级循环网络。

6.3.3 基本的单级互连网络

1. 立方体（Cube）单级网络

N个结点的立方体单级网络共有n=log₂N种互联函数，即：

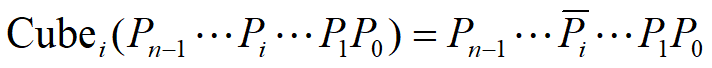
如0000，变换第二位，则变成0100

显而易见，单级立方体网络的最大距离为n，即反复使用单级网络，最多经n次传送就可以实现任意一对入、出端间的连接。而且任意两个结点之间至少有n条不同的路径可以走，容错性强，只是距离小于n的两个结点之间各条路径的长度可能不等。

编号为0,1,…,15的16个处理器，当互联网络函数为Cube₃时，计算13号处理器连接到的处理器的号数是多少？

答：16个结点，每个节点则有n=log₂16=4位
13转化为二进制为1101,Cube₃表示第3位取反，即Cube₃(1101)=0101,
转化为十进制即是和5号处理器连接

2. PM2I单级网络

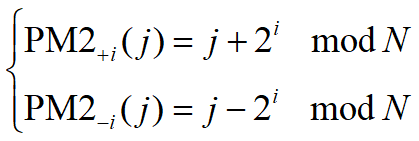
PM2I是加减2单级网络的简称。其中，0≤j≤N-1,0≤i≤n-1,n=log₂N。它共有2n个互联函数。由于PM2_+(n-1)=PM2_-(n-1),因此PM2I互联网络只有2n-1种互联函数是不同的。对于N=8的三维PM2I互联网络的互联函数，有PM2₊₀、PM2_-0、PM2₊₁、PM2_-1、PM2_±2等5个不同的互联函数，它们分别为：
PM2₊₀ : (0 1 2 3 4 5 6 7)
PM2_-0 : (7 6 5 4 3 2 1 0)
PM2₊₁ : (0 2 4 6) (1 3 5 7)
PM2_-1 : (6 4 2 0) (7 5 3 1)
PM2_±2 : (0 4) (1 5) (2 6) (3 7)

以PM2₊₀为例，(0 1 2 3 4 5 6 7)表示0连接到1，1连接到2，2连接到3…，7连接到0。可见在PM2I种，0可以直接连到1、2、4、6、7上，比Cube单级网络只能直接连到1、2、4要灵活。

PM2I单级网络的最大距离为N/2向下取整。由三维PM2I互连网络可以看出，最多只要两次使用，即可实现任意一对入、出端号间的连接。

ILLIAC Ⅳ处理单元的互连也是PM2I的特例，采用了其中的PM2I~±0~和PM2I~±n/2~(即PM2I_±3)4个互连函数。

【1704真题】实现16个处理单元互连的PM2I单级网络。
1.写出所有各种单级PM2I互连函数的一般式
2.3号处理单元用单级PM2I网络可以将数据商传送到哪些处理单元上。

答：
1.
n=log₂16=4，所以一共有8个一般式
PM2₊₀(j)=(j+2⁰) mod 16;
PM2_-0(j)=(j-2⁰) mod 16;
PM2₊₁(j)=(j+2¹) mod 16;
PM2_-1(j)=(j-2¹) mod 16;
PM2₊₂(j)=(j+2²) mod 16;
PM2_-2(j)=(j-2²) mod 16;
PM2₊₃(j)=(j+2³) mod 16;
PM2_-3(j)=(j-2³) mod 16;

0≤j≤15

2.按照如上8个一般式，j=3时，可得出答案分别为4、2、5、1、7、15、11、11，所以3号处理单元可以直接送到1、2、4、5、7、11、15号处理单元上。

3. 混洗交换单级网络

混洗交换单级(Shuffle-Exchange)网络包含两个互联函数，一个是全混(Perfect Shuffle)，另一个是交换(Exchange)。

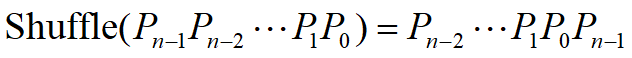
混洗交换其实就是把最高位放在最后去，其中，n=log₂N。

特性：经过n次全混，除全0和全1外，各个处理单元都遇到了与其它多个处理单元连接的机会。

由于单纯的全混互连网络不能实现二进制编号为全0或全1的处理单元与其它处理单元的连接，因此还需要增加Cube~0~交换函数。这就是全混交换单级网络。其中，实现表示交换，虚线表示全混。

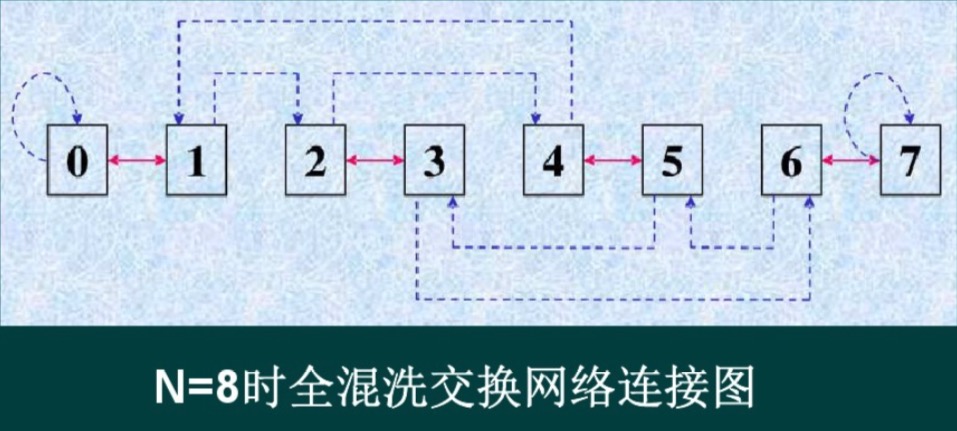
在混洗交换网络中，最远的两个入、出端是全0和全1，它们的连接需要n次交换和n-1次混洗，所以其最大距离为2n-1。

4. 蝶形单级网络

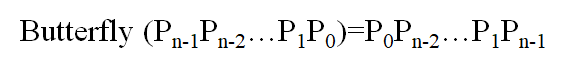
蝶形是将最高位和最低位相互交换位置

0->0,1->4,2->2,3->6,4->1,5->5,6->3,7->7
0->0:000 -> 000
1->4:001 -> 100 
2->2:010 -> 010
3->6:011 -> 110
4->1:100 -> 001
5->5:101 -> 101
6->3:110 -> 011
7->7:111 -> 111

6.3.4 基本的多级互连网络

不同的多级互连网络，在所用的交换开关、拓扑结构和控制方式上各有不同。

交换开关是具有两个入端和两个出端的交换单元，用作各种多级互连网络的基本构建。

无论入端或出端，如果令居于上方的都用i表示，居于下方的都用j表示，则可以定义下列4种开关状态或连接方式。

• 1. 直连，即（i_入）连（i出_），（j入_）连（j出~）
• 2. 交换，即（i_入）连（j_出），（j_入）连（i_出）
• 3. 上播，即（i_入）连（i_出）和（j_出），（j_入）悬空
• 4. 下播，即（j_入）连（i_出）和（j_出），（i_入）悬空

只有前两种功能的称二功能交换单元，有全部四种功能的称四功能交换单元。

拓扑结构是各级间出端与入端互联的模式。

控制方式是对各个交换开关进行控制的方式，以多级立方体网络为例，它可以有个3种：

• 1. 级控制–同一级的所有开关只用一个控制信号控制，同时只能处于同一种状态
• 2. 单元控制–每一个开关都由自己独立的控制信号控制，可各自处于不同的状态
• 3. 部分级控制–第i级的所有开关分别用i+1个信号控制,0<=i<=n-1，n为级数

1.多级立方体网络

多级立方体网络有STARAN网络、间接二进制n方体网络等。它们的共同特点是：第i级(0≤i≤n-1)交换单元处于交换状态时，实现的是Cube_i互连函数，且都采用二功能交换单元。两者的差别仅在于控制方式上，STARAN网络采用级控制(称交换网络)和部分级控制(其中可实现移数功能的称移数网络)，而间接二进制n方体网络用单元控制。因此，后者具有更大的连接灵活性。

STARAN网络用作交换网络时，采用级控制，实现的是交换函数。

2.多级混洗交换网络

多级混洗交换网络又称omega网络。它由n级相同的网络组成，每一级都包含一个全混拓扑和随后一列2^n-1个四功能交换单元，采用单元控制方式。通过比较发现，omega网络中各级编号的次序与多级立方体网络正好相反。如果把omega网络的入断和出端位置对调，它就等同于间接二进制n方体网络。因此，omega网络与间接二进制n方体网络只有两点差别：前者数据流向是级号n-1,n-2,…,1,0,用四功能交换单元；后者数据流向相反，是级号0,1,…,n-1,用二功能交换单元。

互联网络-单级互连网络

分别实现16个处理单元的立方体单级网络、PM2I单级网络、混洗交换单级网络、蝶形单级互连网络。
1)写出所有各种互连函数的一般式。
2)3号处理单元可将数据直接传送到哪些处理单元上？

答：
1)n=log₂16=4
立方体单级网络的一般式为：
Cube₀(P₃P₂P₁P₀)=P₃P₂P₁$\overline{P_0}$
Cube₁(P₃P₂P₁P₀)=P₃P₂$\overline{P_1}$P₀
Cube₂(P₃P₂P₁P₀)=P₃$\overline{P_2}$P₁P₀
Cube₃(P₃P₂P₁P₀)=$\overline{P_3}$P₂P₁P₀

PM2I单级网络的一般式为：
PM2₊₀(j)=j+2⁰ mod 16
PM2_-0(j)=j-2⁰ mod 16
PM2₊₁(j)=j+2¹ mod 16
PM2_-1(j)=j-2¹ mod 16
PM2₊₂(j)=j+2² mod 16
PM2_-2(j)=j-2² mod 16
PM2₊₃(j)=j+2³ mod 16
PM2_-3(j)=j-2³ mod 16
其中0≤j≤15

混洗交换单级网络的一般式为：
Shuffle(P₃P₂P₁P₀)=P₂P₁P₀P₃

蝶形单级网络的一般式为：
Butterfly(P₃P₂P₁P₀)=P₀P₂P₁P₃

2)根据1)中一般式来计算可得出，3号处理单元转换为二进制为0011，所以
立方体单级网络中，
Cube₀时，2号
Cube₁时，1号
Cube₂时，7号
Cube₃时，11号
所以立方体单级网络，3号处理单元可直接传送到的处理单元号为：1、2、7、11

PM2I单级网络中，
PM2₊₀时，4号
PM2_-0时，2号
PM2₊₁时，5号
PM2_-1时，1号
PM2₊₂时，7号
PM2_-2时，15号
PM2₊₃时，11号
PM2_-3时，11号
所以PM2I单级网络，3号处理单元可直接传送到的处理单元号为：1、2、4、5、7、11、15

混洗交换单级网络中，3号处理单元可直接传送到的处理单元号为：6

蝶形单级网络中，3号处理单元可直接传送到的处理单元号为：10

互连网络 - 多级立方体互连网络

阵列有0-7共8个处理单元互连，要求按(0,5),(1,4),(2,7),(3,6)配对通信。
1)写出实现此功能的互联函数的一般式。
2)画出用三级立方体网络实现互连函数的互连网络拓扑结构图，并标出各控制开关的状态。

答：
1)n=log₂8=3,通过观察得知，互连函数的一般式为：f(P₂P₁P₀)=$\overline{P_2}$P₁$\overline{P_0}$

2)图像如下所示：

若要从0入，从5出，则第0级是交换、第1级是直连、第2级是交换

互连网络 - 多级混洗互连网络

给出N=8的蝶式变换，对应关系为(0,0),(1,4),(2,2),(3,6),(4,1),(5,5),(6,3),(7,7)。
1)写出此互连函数的关系式。
2)如果采用omega网络，需几次通过才能完成此变换。
3)列出omega网络实现此变换的控制状态图。

答：n=log₂8=3
1)通过观察得知，互连函数的关系式为Butterfly(P₃P₂P₁P₀)=P₀P₂P₁P₃

如图所示，
(0,0): 0->A上->E上->I上->0
(1,4): 1->B下->H上->K上->4
(2,2): 2->C上->E下->J上->2
(3,6): 3->D下->H下->L上->6
(4,1): 4->A上->E上->I下->1
(5,5): 5->B下->H上->K下->5
(6,3): 6->C上->E下->J下->3
(7,7): 7->D下->H下->L下->7

如上所示，有四个冲突，0和4都要走A上,1和5都要走B下，2和6都要走C上，3和7都要走D下，所以至少需要分成两次通过才可完成此变换。

3)将2)中控制单元中的通路虚线连通即可

6.4 共享主存构型的阵列处理机种并行存储器的无冲突访问

在共享主存构型的阵列处理机种，存储器频宽要与多个处理单元的速率匹配，存储器就必须采用多体并行组成。此外，还要保证存储器无冲突地工作。

情况1

对一维数组而言，假定并行存储分体数m为4，交叉存放一维数组。那么，每次访问相连的m个元素，并依此不间断地访问下去，是不会发生访存冲突的。但是遇到按2变址（按2次幂寻址），访问奇数或偶数下标的元素时，则因访存冲突会使存储器的实际频宽降低一半。因此，并行存储器的分体数m应取成质数，才能较好地避免存储器访问的冲突。只要变址跳距与m互质，存储器访问就总能无冲突地进行。

情况2

对于二维数组（结论也适用于多维数组）而言，假设主存有m个分体并行，从中访问有n个元素的数组子集。这n个元素的变址跳距对于二维数组的行、列、主对角线、次对角线都是不一样的，但要求都能实现无冲突访问。

将二维数组中各元素在存储器中错位存放可以使行或列的各元素都能并行访问，但会造成主对角线上各元素的并行访问冲突。

存储方案：使并行存储器分体数m大于每次要访问的向量或数组元素的个数n（n在阵列处理机上就是处理单元数），且m是一个质数，同时在多维数组的行、列等方向上采取不同的错开距离。

情况3

并行存储器中存放的数组大小是不固定的，多维数组各维的元素个数也不一定相等，它们还可以超出已选定的分体数m的值。

解决方案：将多维数组或者非n x n方阵的二维数组按行或列的顺序变换成一维数组，形成一个一维线性地址空间，地址用a表示。然后，将地址a所对应的元素存放在体号地址j=a mod m,体内地址为i=a/n向下取整 的单元中

6.5 脉动阵列流水处理机

6.5.1 脉动阵列结构的原理

脉动阵列结构是由一组处理单元(PE)构成的阵列。每组PE的内部结构相同，可完成少数基本的算术逻辑运算操作。阵列内所有处理单元的数据锁存器都受同一个时钟控制。运算时数据在阵列结构的各个处理单元间沿各自的方向同步向前推进，就像血液受心脏有节奏地搏动在各条血管中间同步向前流动一样。因此，形象地称其为脉动阵列结构。实际上，为了执行多种计算，脉动型系统内的输入数据流和结果数据流可以在多个不同方向上以不同速度向前搏动。

特点：

• 1. 结构简单、规整，模块化强，可扩充性好，非常适合用超大规模集成电路实现；
• 2. PE间数据通信距离短、规则，使数据流和控制流的设计、同步控制等简单规整；
• 3. 脉动阵列中所有PE能同时运算，具有极高的计算并行性，可通过流水获得很高的运算效率和吞吐率。输入数据能被多个处理单元重复使用，大大减轻了阵列与外界的I/O通信量，降低了对系统主存和I/O系统频宽的要求。
• 4. 脉动阵列结构的构型与特定计算任务和算法密切相关，具有某种专用性，限制了应用范围，这对VLSI是不利的。

6.5.2 通用脉动阵列结构

途径一：增设附加的硬件，可以经程序重新配置阵列的结构。

途径二：用软件把不同的算法映像到固定的阵列结构上。

图中，正方形是控制开关。