并查集概述

并查集详解

最新推荐文章于 2025-08-06 18:21:08 发布

原创最新推荐文章于 2025-08-06 18:21:08 发布 · 451 阅读

0 ·

CC 4.0 BY-SA版权

数据结构专栏收录该内容

35 篇文章

订阅专栏

以前以为并查集是一个比较简单的东西，结果发现oi界啥都不简单。具体可以参见啥输入输出题。（输出自己的程序）。

好了，我们来讲并查集：P1551 亲戚

这是一道入门题，我们可以在有亲戚关系的两个人之间连一条边，然后查询可以从一个人出发看能否走到另一个人。这样我们就得到了一个 $O(mn)$ 的算法。这一道题我们就能过了。

但是并查集有什么卵用咧，其实并查集就是优化这种做法：对于每一块我们指定一个父亲，然后同一块的可以走到同一个父亲对不对？连接的时候就把两个的父亲连在一起。这样在数据随机的情况下，我们就做到了 $mlogn$ 。但是众所周知，出题人是不会让你过的。所以接下来还有两种优化：

1.在连接父亲的时候，把size小的接到size大的上面。这样很好理解，虽然有一个高大上的名字：启发式合并。不过启发式不都这么玄学么。

2.一般式的并查集都带有这么一个优化：路径压缩。假如每次都查询一个离父亲很远的两个点，我们的复杂度就爆表了。但是在从自己向父亲跳的步骤是没有什么卵用的，于是我们考虑既然我们已经找出了某一点的父亲，那我们可以直接把这个点连在父亲上了。画个图，我最喜欢画图了：

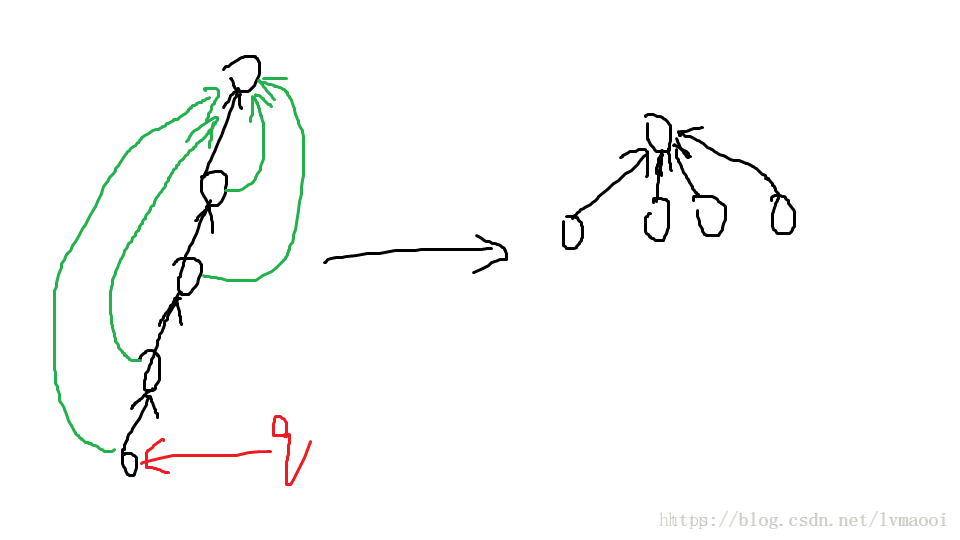
这里写图片描述

看，每次就把查询的一整条链拆开把链上所有的连到父亲上。下一次对这条链上的查询就可以做到 $O(1)$ 。然后这样我们就可以做到接近 $O(n)$ 完成所有操作。但是虽然这样做很快，但是有一个弊端，就是我们不能可持久化，不能撤销的。不过~~并查集本身就不怎么支持撤销操作，可持久化是非常蛋疼的，所以对于普通的并查集这么写就行了。

值得注意的是，写路径压缩我们最好使用递归写法，因为非递归确实比递归长得多。

另外可以使用并查集的每一个父节点记录整个并查集的信息。或者使用每一个节点记录它到父节点链上的信息。

贴一份代码：

#include<iostream>  
#include<cstdio>  
using namespace std;  
int fa[20005];  
int find(int p)//找父亲  
{  
    if(fa[p]==p)//如果是父亲，就返回自己  
      return p;  
    return fa[p]=find(fa[p]);//把这个点指向父亲，并返回父亲  
}  
void com(int a,int b)//连接  
{  
    a=find(a);  
    b=find(b);  
    fa[a]=b;  
}  
int main()  
{  
    int n,m,a,b,rt1,rt2,q;  
    cin>>m>>n>>q;  
    for(int i=1;i<=m;i++)//初始化，自己叫自己爸爸，有时候容易忘  
      fa[i]=i;  
    for(int i=1;i<=n;i++)  
    {  
        cin>>a>>b;  
        com(a,b);  
    }  
    for(int i=1;i<=q;i++)  
    {  
        cin>>a>>b;  
        rt1=find(a);  
        rt2=find(b);  
        if(rt1==rt2)  
          cout<<"Yes"<<endl;  
        else  
          cout<<"No"<<endl;  
    }  
}

特别短啊，有木有？真正有用的其实就是找爸爸那四行。
$\\$

这样就完了？naive！！！

并查集还有一种应用：P3865 【模板】ST表

对，我们拿着并查集的板子去干st表的板子，有没有很兴奋咧？

我们思考5分钟~~~

思考！！！

嗯，那你肯定会做了对不对？看看和标算一不一样。首先我们把所有询问按右端点从小到大排序。我们每次区间询问就把区间处理之后把区间中的每一个点连向右端点，每个节点记录它到它到祖宗中的最大值。

我们画个图看看：

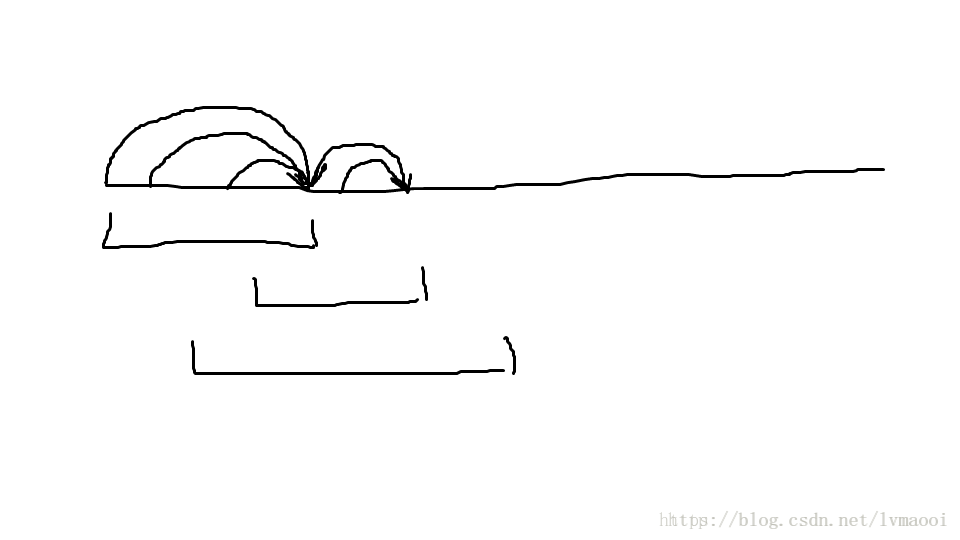
这里写图片描述

虽然我们一次的复杂度可能是 $O(n)$ 的，但是之后每一次查询可以从左端点跳到已经处理过的最远点。再画个图看看：

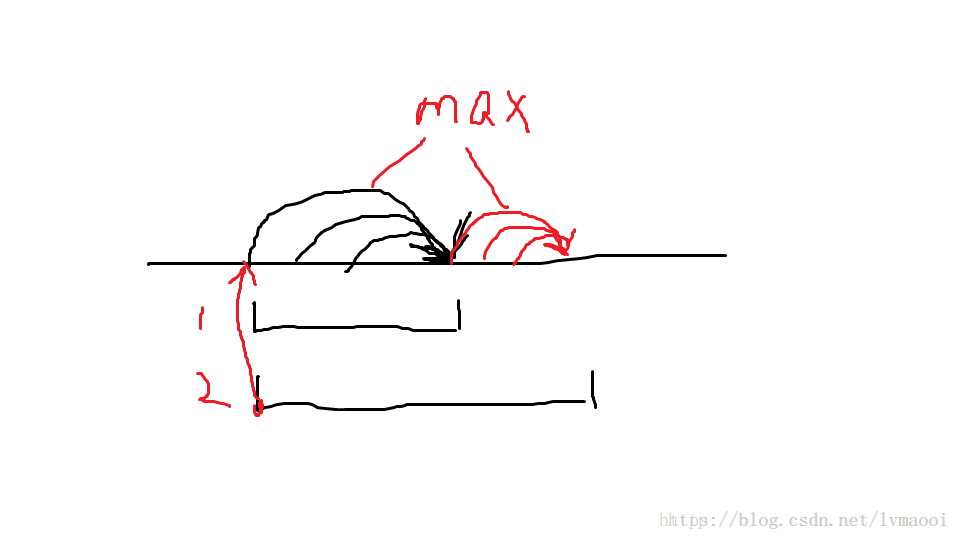
这里写图片描述

很容易可以看出，每个点最多处理1次，而并查集复杂度接近 $O(n)$ ，也就是说每跳一次复杂度可以看做 $O(1)$ 。所以如果基数排序的复杂度也是 $O(n)$ 的，那么总复杂度是 $O(n)$ 。

再理解一下，就是所有求过最大值的区间我们可以使用并查集 $O(1)$ 跳过。然后我们发现链上取最大值信息是可以合并的。所以我们可以做到路径压缩。

这就是并查集的另一种应用，在区间上可以 $O(1)$ 跳到最近的没有到达过的点，然后可以做到 $O(n)$ 对区间处理一些信息。

贴一下代码：

#include<iostream>  
#include<cstdio>  
#include<cstring>  
#include<cmath>  
using namespace std;  
struct lxy{  
    int id,l,r,ans;  
}b[1000005];  

int fa[100005];  
int num[100005];  
int n,m;  
lxy bi[1000005];  
int ret[1000005];  
int tax[100005];  

int readit()  
{  
    char x;int a=0;  
    x=getchar();  
    while(x<'0'||x>'9') x=getchar();  
    while(x>='0'&&x<='9') a=a*10+x-'0',x=getchar();  
    return a;  
}  

int findit(int x)//主要是这里，  
{  
    if(x==fa[x]) return x;  
    int y=findit(fa[x]);  
    num[x]=max(num[x],num[fa[x]]);  
    return fa[x]=y;  
}  

void rsort()  
{  
    for(int i=1;i<=m;i++) tax[bi[i].r]++;  
    for(int i=1;i<=n;i++) tax[i]+=tax[i-1];  
    for(int i=m;i>=1;i--) b[tax[bi[i].r]--]=bi[i];  
}  

int main()  
{  
    n=readit();m=readit();  
    for(int i=1;i<=n;i++) num[i]=readit(),fa[i]=i;  
    for(int i=1;i<=m;i++) bi[i].l=readit(),bi[i].r=readit(),bi[i].id=i;  
    rsort();  
    for(int i=1;i<=m;i++)  
    {  
        for(int j=b[i].l;j<=b[i].r;j++)//虽然说图上是直接连到右端点，但是不好写，我们选择常数大一点的方法，连向它右边的点，最后路径压缩就可以全部连向右端点  
        {  
            j=findit(j);//跳到父亲，只连父亲就相当于把前面的都连了  
            if(j!=b[i].r) fa[j]=j+1;  
        }  
        findit(b[i].l);//路径压缩  
        b[i].ans=num[b[i].l];  
    }  
    for(int i=1;i<=m;i++)  
      ret[b[i].id]=b[i].ans;  
    for(int i=1;i<=m;i++)  
      printf("%d\n",ret[i]);  
}

这样就完了？naive！！！

最近发现并查集还有一种应用：P1640 [SCOI2010]连续攻击游戏

虽然是一道省选题，然而要是会了并查集这种应用就很简单了。

“这个并查集做法真是把我惊呆了，完全没有想到”——蒟蒻的我

并查集怎么做呢，感觉和并查集没什么关系啊。但是我们先可以思考一个问题：用并查集判断是否存在环。

很简单可以发现如果一个并查集内有一个连边，在这个并查集内就会出现一个环（很显而易见对吧）。否则这个并查集就是一个类似于树的结构，除非它自己内部多出了一条连边。

然后我们观察这道题的性质，会发现一个结论：对一个装备的两个值连边，最后一个大小为p的并查集内有p-1个数可以被选到，另外的，如果并查集里有环，并查集里都可以选。

画一个图看看：

这里写图片描述

我们可以想象一个图是由“—O”这种符号组成的。所以这个性质很厉害的是：对于每一个无环图，我哪一个点不选都是可以做到的。所以我们维护并查集&并查集中是否有环。

然后从1向后查，判断是否可以在并查集中被取到，如果取不了就break；

附上代码：

#include<iostream>  
#include<cstdio>  
#include<cstring>  
using namespace std;  

int fa[10005],vis[10005],num[10005];  
int n,ans=1;  

int find(int x)  
{  
    if(x==fa[x]) return x;  
    return fa[x]=find(fa[x]);  
}  

int main()  
{  
    scanf("%d",&n);  
    for(int i=1;i<=10000;i++) fa[i]=i,num[i]=1;  
    for(int i=1;i<=n;i++)  
    {  
        int x,y;  
        scanf("%d%d",&x,&y);  
        x=find(x);  
        y=find(y);  
        if(x==y)  
        {  
            vis[x]=1;  
            continue;  
        }  
        else fa[x]=y,num[y]+=num[x];  
    }  
    while(ans<=10000&&(--num[find(ans)])+vis[find(ans)]) ans++;  
    printf("%d",ans-1);  
}