一、特殊关系
-
等价关系(类似于分类)

Eg:

-
等价类

Eg:
2.1)等价类的性质

-
商集

Eg:

-
集合的划分
4.1)定义

Tips:

4.2)集合划分->等价关系
Eg:

-
偏序(类似于排序)
5.1)定义

Tips:

Eg:

tips:

5.2)可比与覆盖
5.2.1)定义

Eg:

-
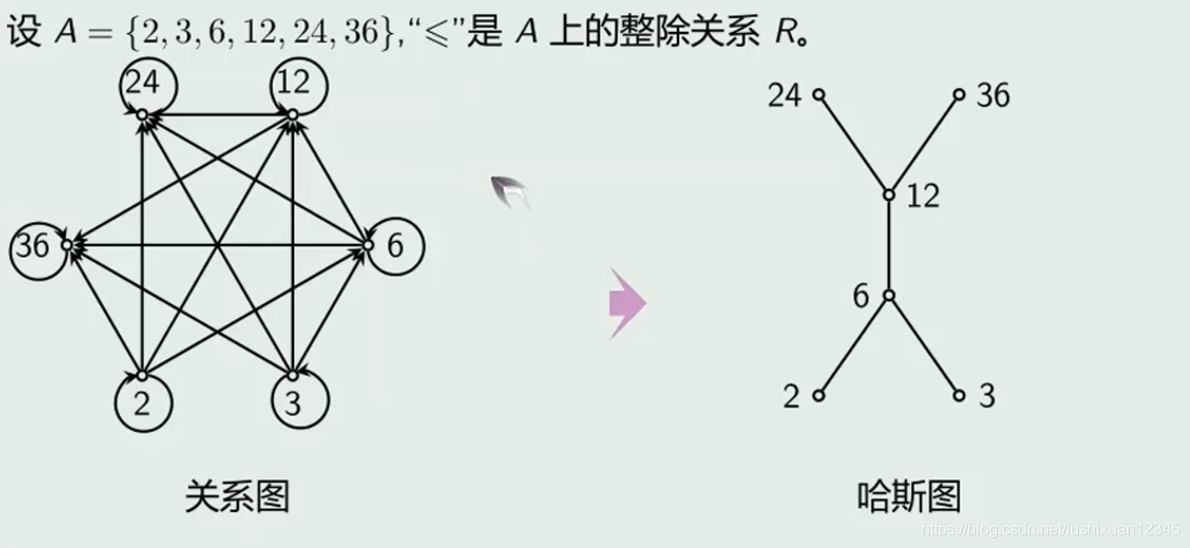
哈斯图
1)定义

Eg:
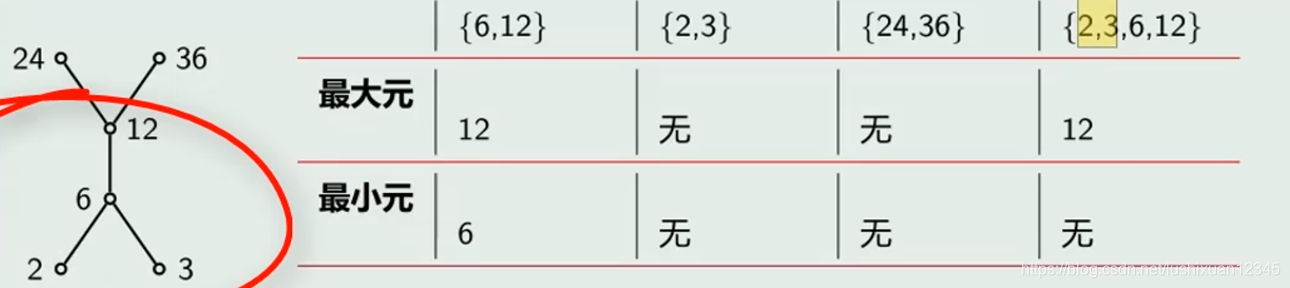
2)最大元与最小元
2.1)
Eg:
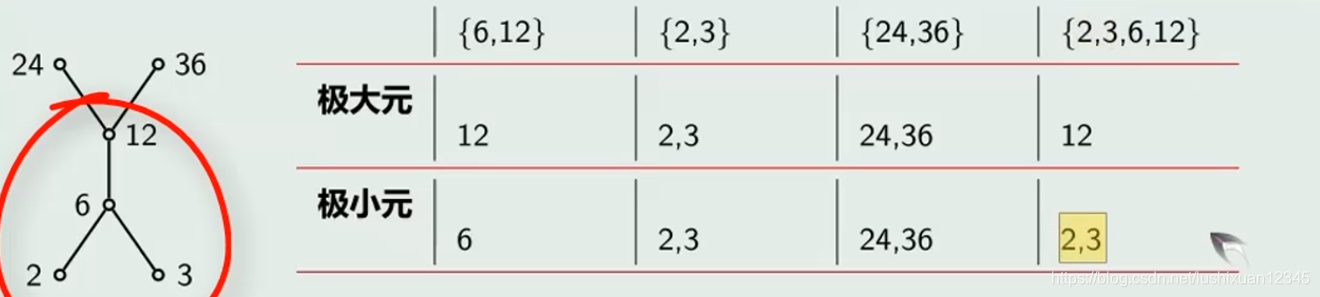
3)极大元与极小元
3.1)定义

Eg:
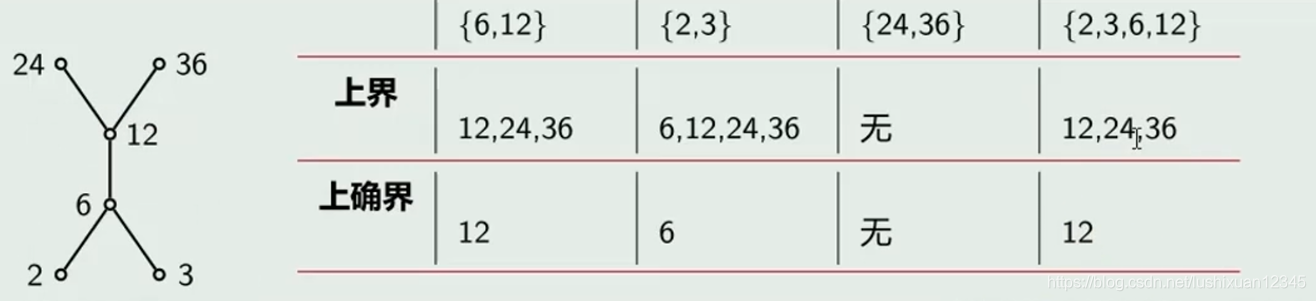
4)上界和上确界

Eg:
5)极大元与极小元
5.1)下界和下确界

Eg:
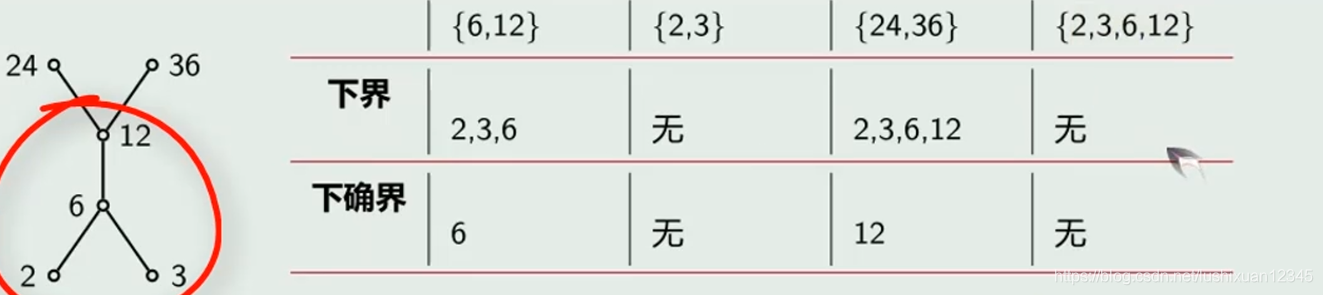
Tips:

-
其他次序关系
7.1)拟序关系
7.1.1)定义

Eg:

7.2)全序关系
7.2.1)定义
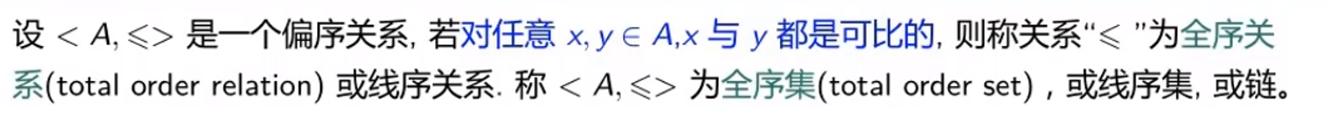
Eg:

7.2.2)全序关系的哈希图
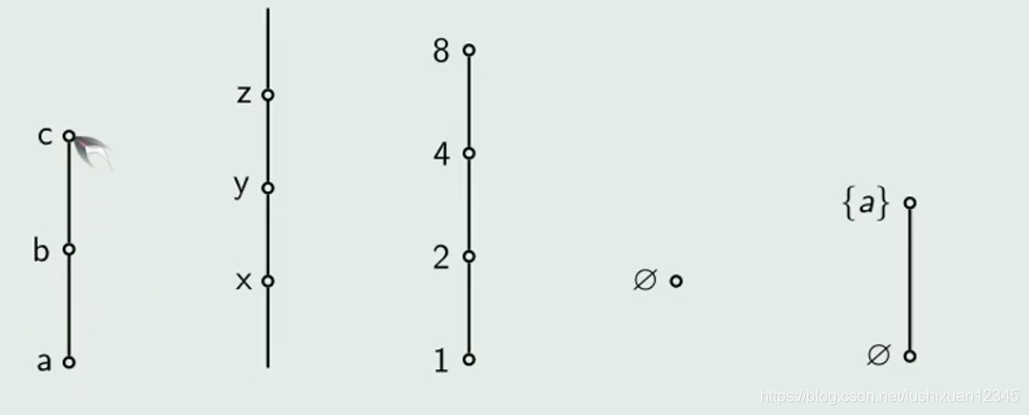
7.3)良序关系

Eg:

Tips:总结

二、图
-
无序对和无序积
1.1)定义
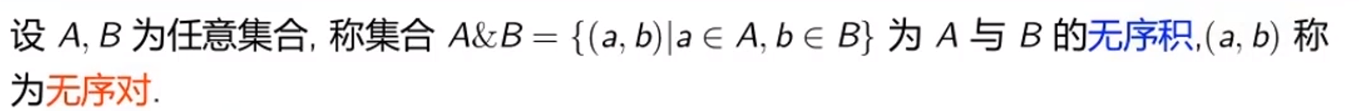
Tips:
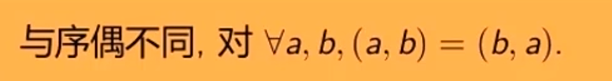
Eg:

-
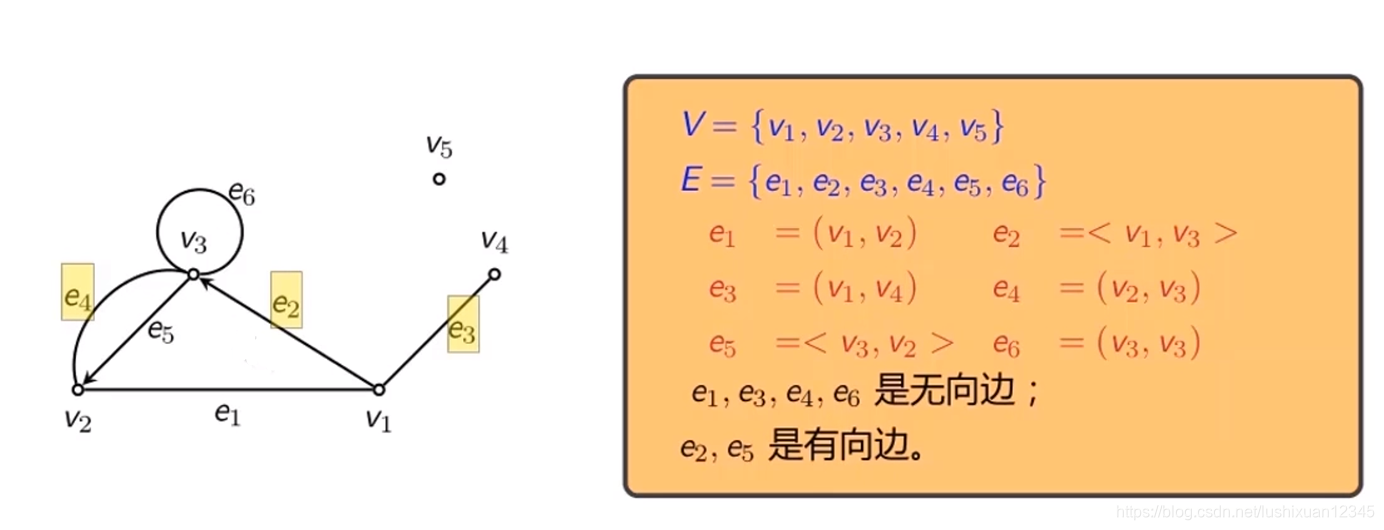
图
2.1)定义

Tips:

Eg:
-
图的表示
3.1)图的表示
Eg:
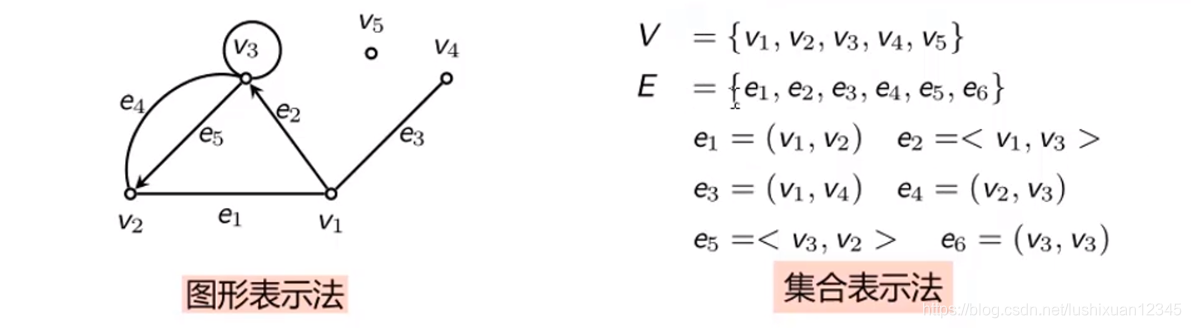
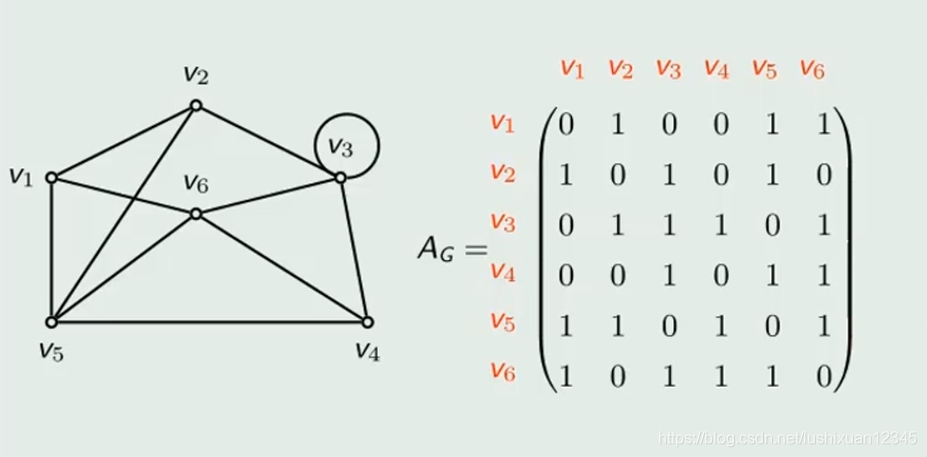
3.2)邻接矩阵

Eg:
3.3)邻接点与邻接边

Eg:

-
图的分类
4.1)定义

Eg:
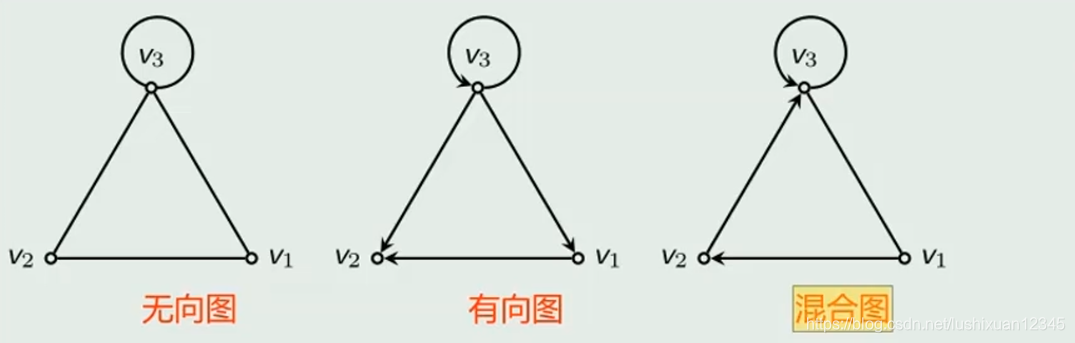
4.2)按照边来分

Eg:

4.3)按照权值来分

-
子图与补图
5.1)子图

Eg:
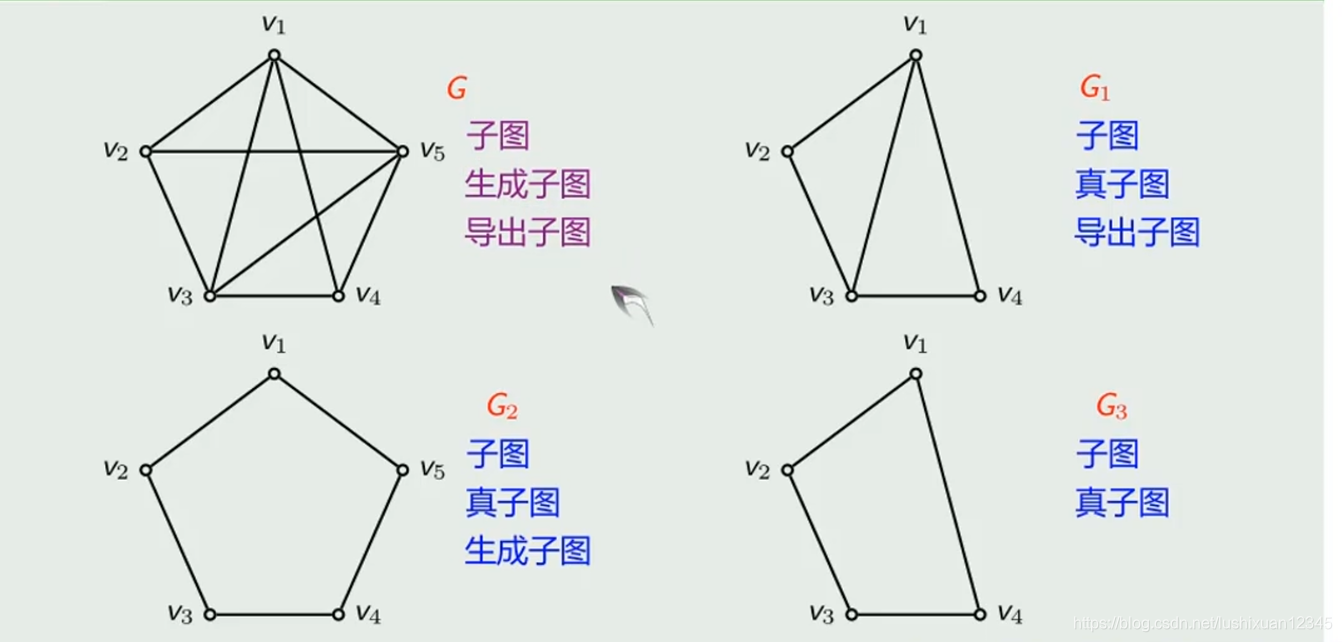
5.2)完全图

5.3)补图
5.1.1)

Tips;

Eg:
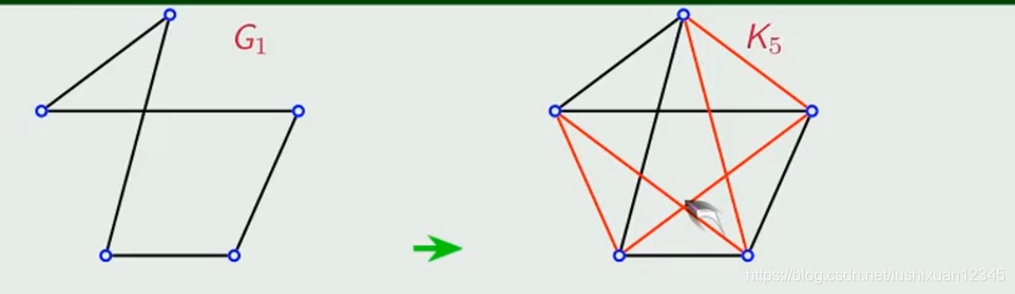
Tips:

5.2)补图的邻接矩阵
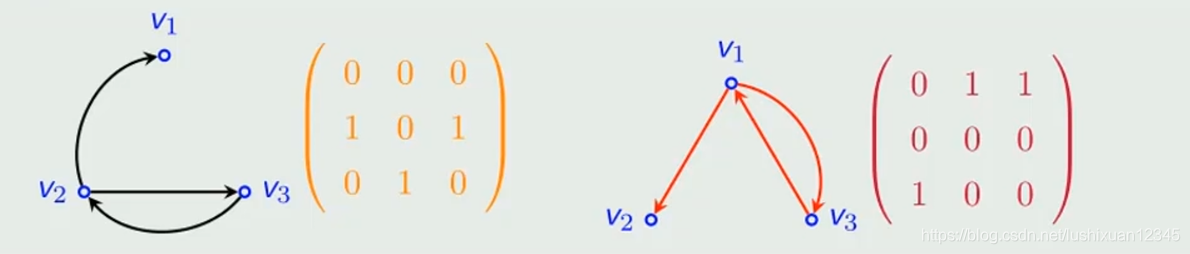
-
握手定理
6.1)结点的度数
6.1.1)定义


Eg:

6.1.2)

6.1.3)邻接矩阵计算度数
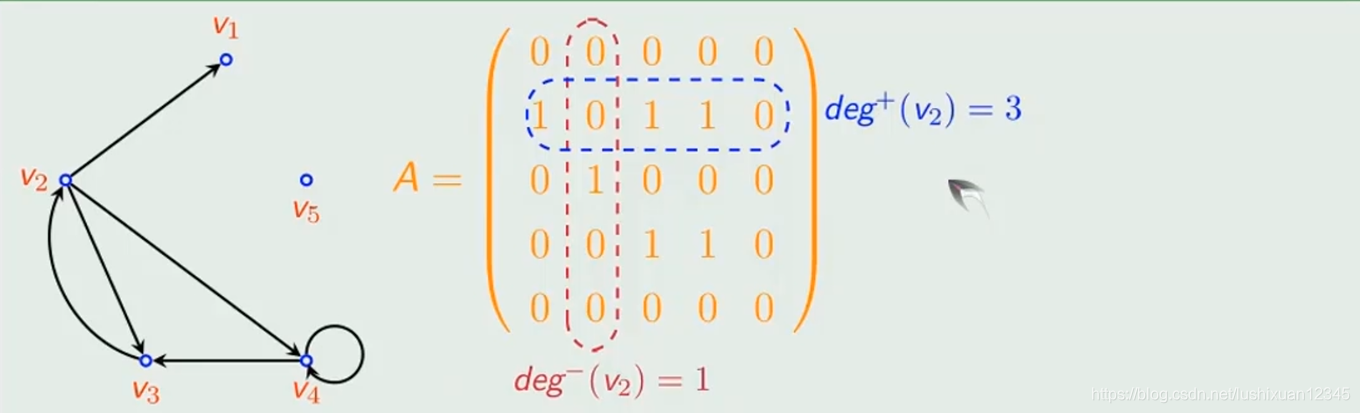
6.2)握手定理
6.2.1)定义

Eg:


6.3)握手定理
6.3.1)图的度数序列

Eg1:
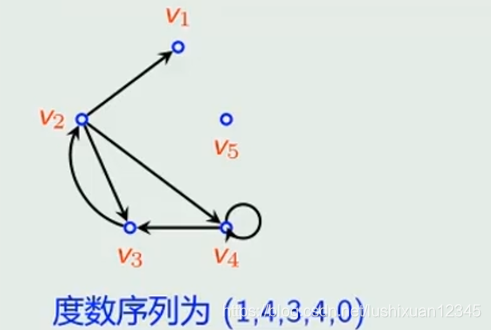
Eg2:

Tips:图的度数序列中奇结点的度数一定是欧式 -
图的同构

Tips:

Eg:
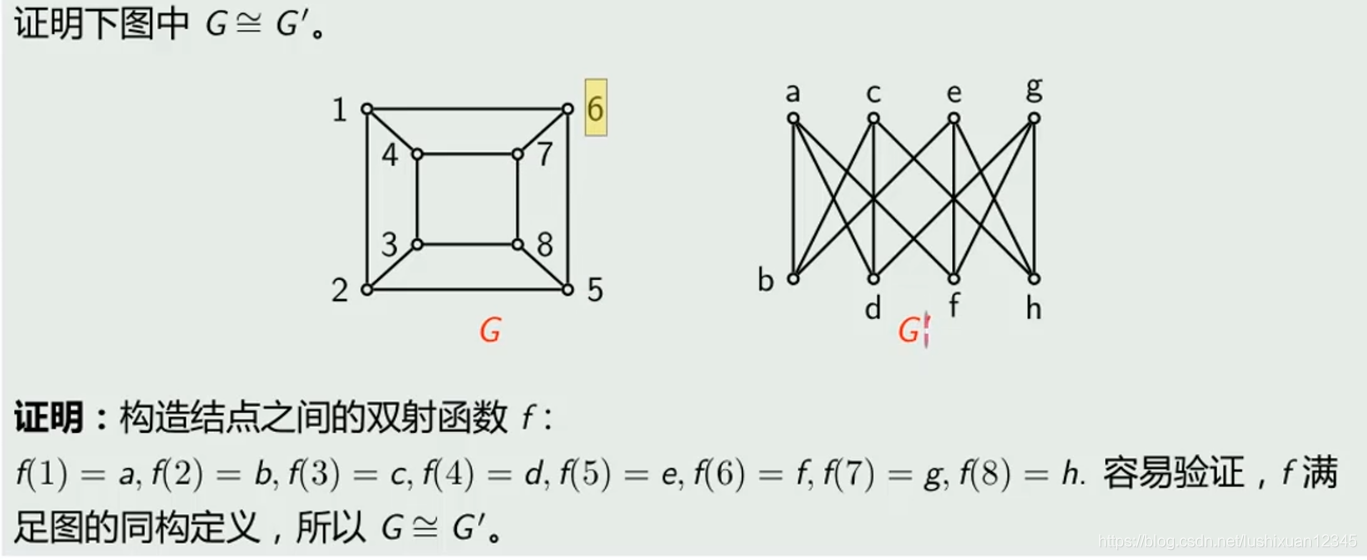
-
通路与回路
8.1)通路定义

Eg:

8.2)通路数量的计算

Eg:
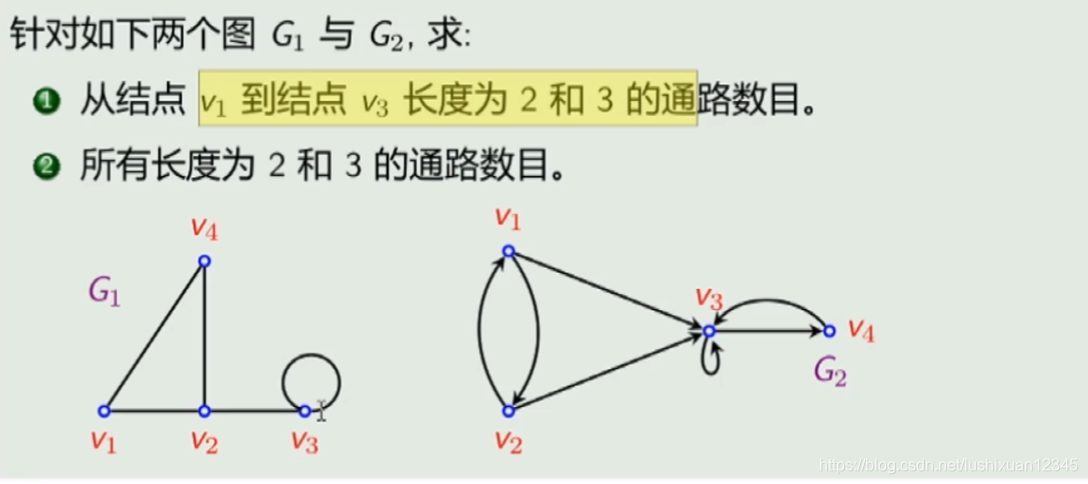

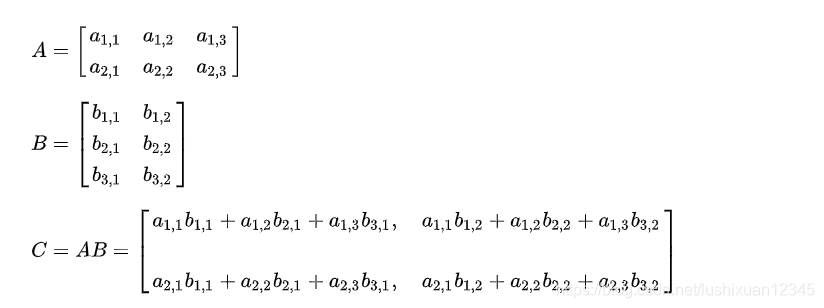
-
可达性与最短通路
9.1)可达性
9.1.1)定义

9.1.2)判定


Eg:

9.2)最短路程
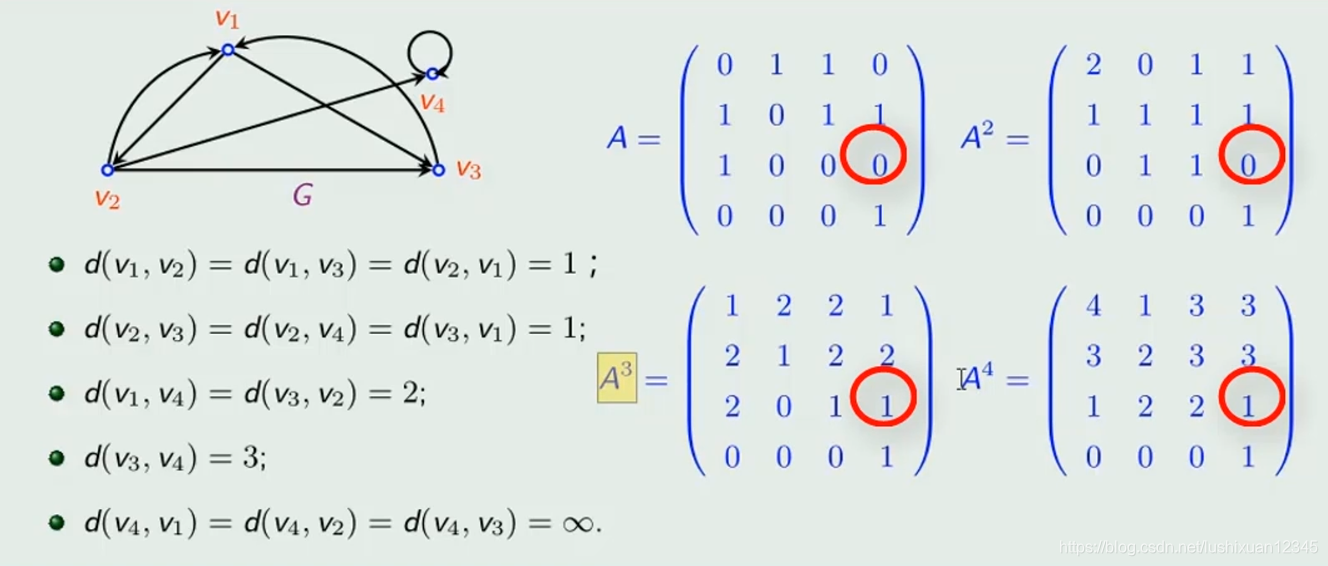
-
无向图的连通性
10.1)定义

10.2)连通分支

Eg:
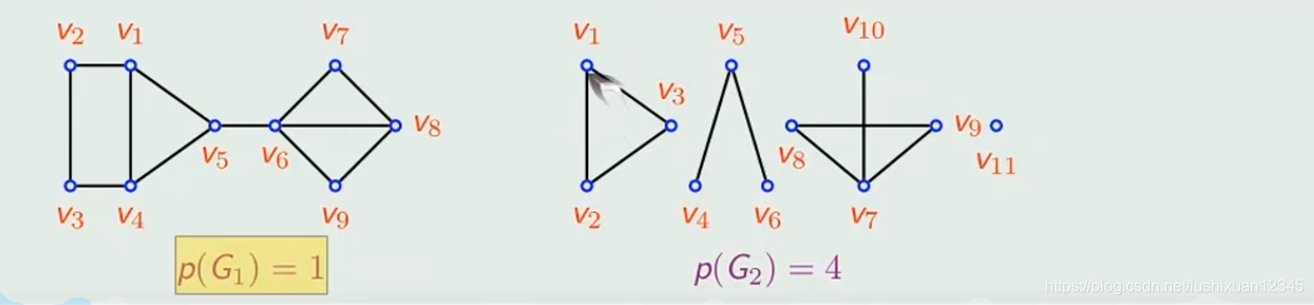
10.3)点割集、边割集
10.3.1)定义

Eg:


10.3.2)连通度

Eg:

-
有向图的连通性
11.1)定义

Eg:
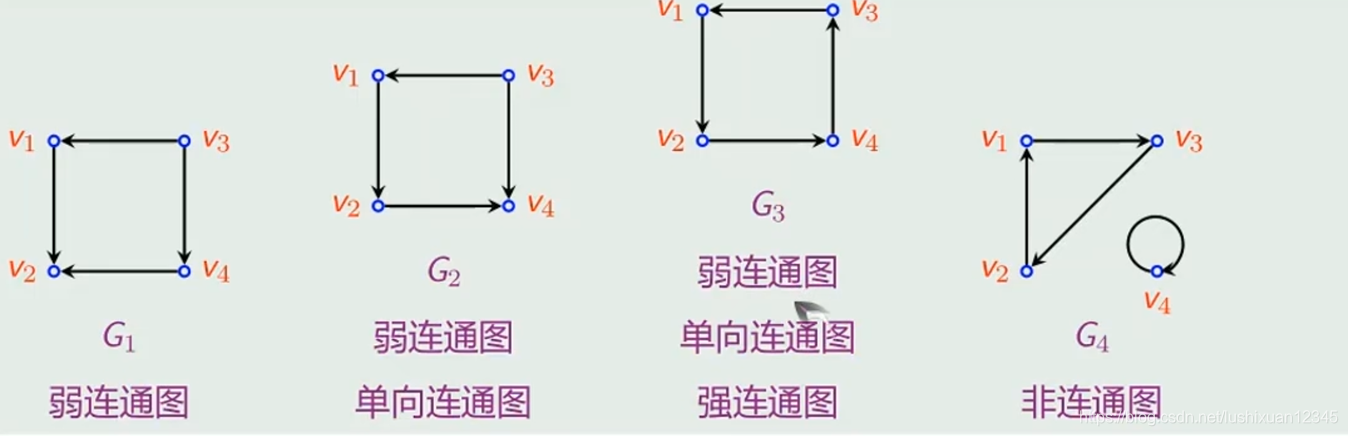
11.2)强连通图
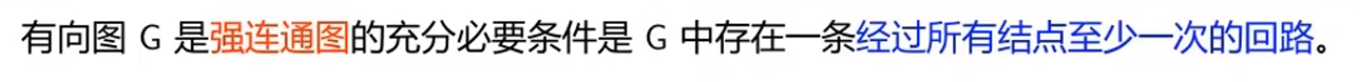
Eg:

Tips:

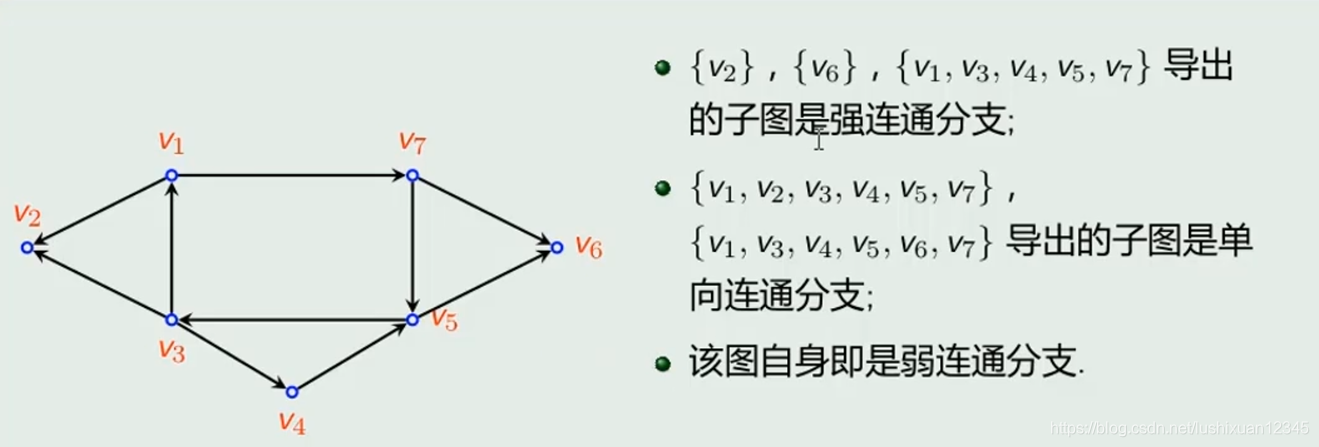
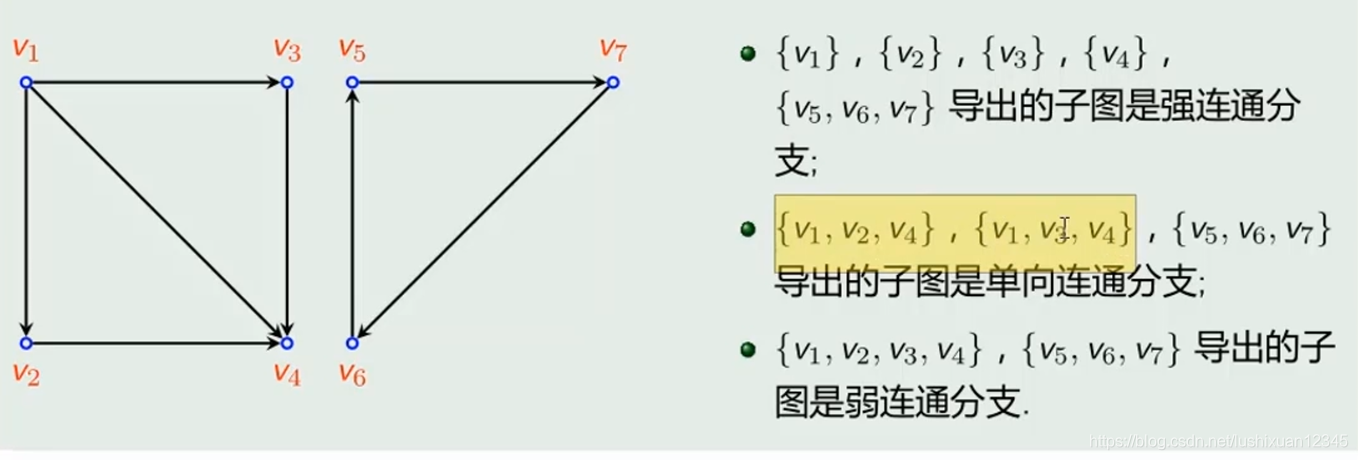
11.3)三类连通图
11.3.1)定义

Eg1:
Eg2:
























 2万+
2万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








