深度学习——单层感知器从原理到实践

单层感知器

首先我们从人工神经网络第一次兴起的单层感知器谈起。

1.工作原理

感知器（perceptron），有的也称其为感知机，是人工神经网络中最基础的网络结构（perceptron一般特指单层感知器，而多层感知器一般被称为MLP）。

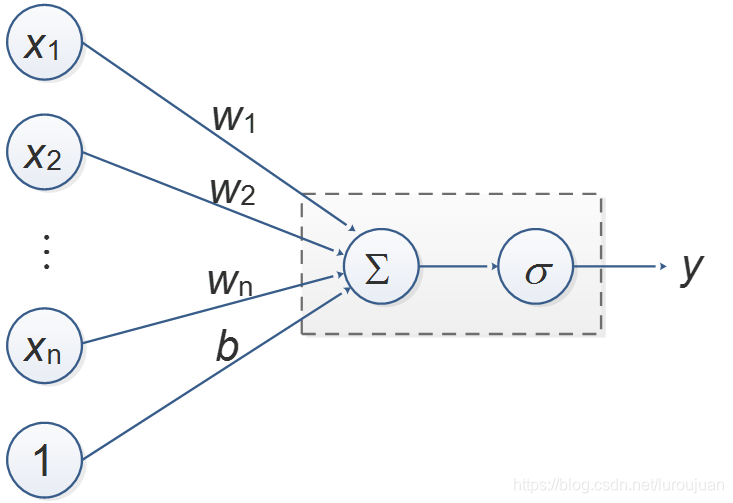
下图给出了一种单层感知器的模型，可以用公式表示为

其中X代表向量[x1,x2,…,xn,1]，W代表向量[w1,w2,…,wn,b]，σ代表激活函数。

对于一组输入值X，我们期望该网络的输出值为Y，而实际输出值为y，则我们定义损失函数（或者称为代价函数、目标函数）L为：

其中的X和Y都是已知值，可见L是关于W的函数。如果我们通过改变W，使得L等于0或者无线趋近于0，则此时可以认为网络的输出值y就等于期望值Y。那么如何更改W呢？一种方法是梯度下降法：先确定一个初始值，然后将W沿着梯度下降的方向进行调整，就会使得L的值向更小的方向进行变化。

为了更直观的理解，我们将上式中的X看做一个数3，Y也是一个数9，σ函数为y=x。则

用图像表示L与W的关系如下图

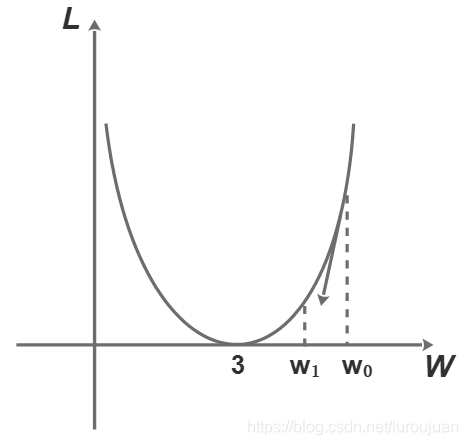
初始值W为w0=6，此时L值为40.5。而在w0处的梯度值d（导数值）为-3*(9-3w0)=27，则沿着梯度下降方向调整到w1处，w1= w0-0.1*d=3.3，将w1代入求得L为0.405。可见L的值