【每日文献阅读】Bridging the Gap: A Decade Review of Time-Series Clustering Methods

原创于 2025-10-24 09:39:20 发布 · 1.2k 阅读

14 ·

CC 4.0 BY-SA版权

文章标签：

#1024程序员节

文献阅读专栏收录该内容

75 篇文章

订阅专栏

Bridging the Gap: A Decade Review of Time-Series Clustering Methods

JOHN PAPARRIZOS, The Ohio State University, USA
FAN YANG, The Ohio State University, USA
HAOJUN LI, The Ohio State University, USA

摘要

时间序列作为序列数据最基础的表示形式之一，已在计算机科学、生物学、地质学、天文学和环境科学等多个学科领域得到广泛研究。先进传感、存储和网络技术的出现催生了高维时间序列数据，但这也为分析长期时间尺度下的潜在结构带来了重大挑战。时间序列聚类作为一种成熟的无监督学习策略，可将相似时间序列归为一类，有助于揭示这些复杂数据集背后的隐藏模式。本文综述了时间序列聚类方法从经典方法到神经网络最新进展的演变过程。以往综述多聚焦于特定方法类别，而本文则搭建了传统聚类方法与新兴深度学习算法之间的桥梁，为该研究领域提出了一个全面、统一的分类体系。此外，本文还重点阐述了该领域的关键进展，并为未来时间序列聚类研究提供了参考思路。

关键词：时间序列数据；聚类；数据挖掘；表示

1 引言

时间序列是由实值数据构成的有序序列，已被广泛认为是最基础的数据格式之一。随着传感、存储、网络和数据挖掘技术的发展，海量原始数据能够被实时获取、存储和处理[174, 181]。凭借时间上的先后表示优势，时间序列的应用几乎遍及所有科学领域或行业[74, 102, 126, 140, 151, 166, 185, 186, 249]，包括但不限于：环境领域[99, 123, 216]、生物学领域[220, 239, 268]、金融领域[4, 64, 79, 217]、心理学领域[129]以及人工智能领域[227]。然而，在信息时代，包含数千甚至数百万维度的大规模数据日益普遍。这不仅引入了新的复杂性，需要高效的自适应解决方案[53, 104, 105, 147, 148]，还为各类任务中时间序列间潜在关系的分析带来挑战，例如索引[54, 176, 182, 183, 187, 212]、异常检测[31–36, 149, 150, 175, 180, 222]、聚类[18, 178, 179, 184]、分类[177, 211]和预测[188]。

聚类是无监督机器学习领域最早提出的概念之一，被证明是揭示原始数据潜在结构的最有效工具之一。聚类的核心目标是对给定的多个对象进行划分，使同一类内部的相似性最大化，而不同类之间的相似性最小化。换句话说，一组“相似”的数据样本被视为一个簇。因此，每个簇内对象的特征构成了数据集中的模式，即簇内样本共有的特征。例如，在计算机视觉任务中，模式可能是相似对象的某种边缘或颜色特征[153]；而在时间序列领域，不同时间步上的快速增长或下降位置可能具有实际意义。一方面，具有相同模式的数据样本之间距离较小，因此会被划分到同一个簇中；另一方面，优良的聚类策略反过来也有助于寻找这些代表性特征。图1展示了不同领域和应用中的时间序列聚类示例。

在这里插入图片描述

（a.1）正常原型（a.2）局部缺血原型
（星光曲线数据集示例：造父变星（CEP）、食双星（EB）、天琴座RR型变星（RRL）的聚类结果）
（a）心电图（ECG）数据集示例

（左：异常检测，右：索引）
（c.1）异常示例（c.2）聚类结果
（c）用于异常检测的聚类
（d.1）簇I （d.2）簇II
（d）用于时间序列索引的聚类

图1 不同领域和应用中的时间序列聚类示例

k-Means算法[161]是最著名的聚类方法之一，它基于期望最大化（EM）策略，在每次迭代中通过欧氏距离寻找中心点（medoid）和聚类分配。其优良性能使其在电气工程、计算机科学、生物学和金融等多个领域得到应用。然而，k-Means等传统方法在时间序列领域的性能显著下降。研究表明，欧氏空间中的传统度量方法难以处理时间序列数据中的多种变形（包括偏移、缩放和遮挡）[178]，而这些变形在实际场景中十分常见。为解决这一问题，研究者提出了多种方法，这些方法能够对固有变形保持不变性，并对噪声或异常值具有鲁棒性。例如，动态时间规整（DTW）[46]提出了一种弹性度量方法，用于处理多对多对齐问题，并找到使两个序列总距离最小的最优规整路径。为进一步降低计算成本，k-Shape[178]引入了两部分创新：（1）时间复杂度为 $O(n\log(n))$ 的基于形状的距离（SBD）；（2）一种源于优化问题的新型质心计算方法，该方法在聚类任务中实现了显著性能提升[178, 184]。近年来，深度学习时代涌现出大量聚类方法，受到广泛关注。对比学习等多种无监督学习策略使神经网络能够在低维空间中生成具有代表性的特征，这极大地减轻了后续任务（如相异度度量和质心计算）的压力。借助并行计算策略和先进的GPU资源，聚类模型的训练和部署时间大幅缩短。

以往综述[3, 143]探讨了数十年间提出的时间序列聚类算法，并从数据表示、相异度度量、聚类方法和评估指标等多个角度提供了见解。然而，如前所述，许多综述要么仅讨论深度学习时代之前的传统时间序列聚类[3, 143]，要么主要聚焦于端到端深度表示学习[130]。文献[7]综述了传统时间序列聚类工作和早期深度聚类方法，但主要聚焦于生物时间序列聚类的案例研究，未对上述两方面进行全面探讨。据我们所知，本文首次尝试搭建传统时间序列聚类方法与深度学习模型之间的桥梁，为每个类别中的各类时间序列聚类方法提出了新颖且全面的分类体系。我们期望本文能为下一代聚类算法的设计提供有价值的参考。

2 时间序列聚类概述

本节首先介绍时间序列数据的定义，以及单变量与多变量时间序列的区别；随后阐述时间序列聚类的问题定义和聚类过程的通用流程，为后续章节提出的新型分类体系奠定基础。

2.1 时间序列数据的定义

时间序列数据可根据其主要特征进行分类。从维度角度，可分为单变量、多变量和张量场三类；此外，根据数据采集过程中的采样策略，时间序列数据可分为规则采样和不规则采样两类。下文将详细探讨各类时间序列数据，并给出时间序列数据的正式定义。

定义2.1（时间序列）：时间序列 $x_i$ 定义为包含 $T > 1$ 个时间步的观测序列，即 $x_i = \{x_{i1}, x_{i2}, ..., x_{iT}\}$ ，其中 $x_{it} \in \mathbb{R}^d$ 。根据维度 $d$ 的不同，时间步 $t$ 处的每个观测值 $x_{it}$ 可以是实数值（ $d = 1$ ）或向量（ $d > 1$ ）。

定义2.2（子序列）：给定时间序列 $x_i = \{x_{i1}, x_{i2}, ..., x_{iT}\}$ （其中 $x_{it} \in \mathbb{R}^d$ ），子序列 $C_i$ 定义为从 $x_i$ 中提取的连续时间步序列，即 $C_i = \{x_{im}, x_{i(m+1)}, \cdots, x_{i(m+L-1)}\}$ ，其中 $L$ 为子序列长度，且 $\leq m \leq T+1-L$ 。

定义2.3（滑动窗口）：给定时间序列 $x_i = \{x_{i1}, x_{i2}, ..., x_{iT}\}$ （其中 $x_{it} \in \mathbb{R}^d$ ），滑动窗口定义为通过在当前时间序列 $x_i$ 上滑动长度为 $L$ 的“窗口”所提取的一组子序列，滑动步长为 $s$ （满足 $\leq L \leq T-1$ 且 $\leq s \leq T-L$ ）。滑动窗口矩阵的大小为 $\left(\left\lfloor\frac{T-L}{s}\right\rfloor + 1, L\right)$ 。

2.1.1 单变量与多变量时间序列

由上述定义可知，可根据每个时间步观测值的维度将时间序列分为单变量和多变量两类。单变量时间序列（UTS）是一维（ $d = 1$ ）实值数据的有序序列，例如UCR数据集[40]中的ECG200数据集包含200条来自同一患者的心电图记录，每条记录均表示一次心跳过程中电活动的变化。与单变量时间序列不同，多变量时间序列（MTS）的观测值维度大于1（ $d > 1$ ），例如UEA数据集[14]中的PenDigits数据集记录了书写者绘制0-9数字时 $x$ 坐标和 $y$ 坐标的变化轨迹。相较于单变量时间序列，为多变量时间序列设计的方法需要处理多通道间的依赖关系，这增加了多变量时间序列聚类任务的复杂性和挑战性。

图2展示了单变量和多变量时间序列的聚类示例，强调了在设计多变量时间序列聚类算法时需考虑所有通道时间步的重要性。该图左侧表明，通过观察两条单变量时间序列的峰值数量差异，可直接将其分为两个不同的簇；而右侧则显示，若仅使用单个通道（即单变量时间序列）的规则对两条多变量时间序列进行聚类，结果并不理想。相反，多变量时间序列聚类算法需综合考虑所有通道的影响，以确保聚类准确性。
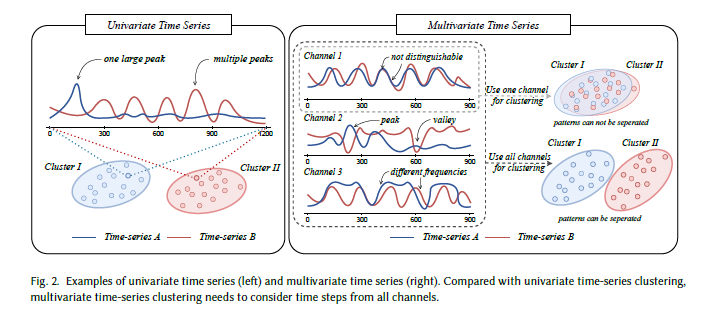
在这里插入图片描述

图2 单变量时间序列（左）和多变量时间序列（右）示例。与单变量时间序列聚类相比，多变量时间序列聚类需考虑所有通道的时间步。

2.2 时间序列聚类的定义

聚类作为机器学习领域的早期概念，已在时间序列领域得到广泛应用。聚类的总体目标是对不同数据样本进行分组，使同一组内样本的距离（或相异度度量）最小化，而不同组间样本的距离（或相异度度量）最大化。该聚类过程不仅为整个数据集提供了一种特定的划分方式，还有助于理解数据的潜在结构，并为时间序列分类、分割、异常检测等下游任务提供有力支持。以下是时间序列聚类的详细定义。

定义2.4[3]：给定包含 $N$ 个时间序列数据的数据集 $\{x_1, x_2, \cdots, x_N\}$ （其中 $x_i \in \mathbb{R}^{d \times T}$ ），时间序列聚类的过程是将 $X$ 划分为 $K$ 个簇 $\{c_1, c_2, \cdots, c_K\}$ （满足 $K < N$ ）。通常，基于预定义的相异度度量，将具有相似特征的同类时间序列数据归为一类。

根据聚类范围，时间序列聚类方法可分为三类[3]：全时间序列聚类、子序列聚类和时间点聚类。

全时间序列聚类：给定一组时间序列，将每条时间序列单独划分为不同的簇。在此过程中，所有时间步均参与相异度度量，以确定样本间的内部和外部关系。
子序列聚类：给定一条时间序列，子序列聚类是指对通过滑动窗口提取的一组子序列进行聚类的过程。
时间点聚类：给定一条时间序列，时间点聚类根据时间邻近性和数值相似性将所有时间点划分为多个组。

然而，文献[3]的讨论指出，这三类时间序列聚类并非都具有实际意义。例如，时间点聚类与时间序列分割的差异极小，主要区别在于聚类过程中可能会将部分时间点视为噪声而剔除。文献[115]的研究表明，子序列聚类在实验中可能产生随机结果，要生成有意义的簇，需要满足现实场景中难以实现的特定条件[115]。图3展示了全时间序列聚类与子序列聚类的区别。因此，本文将重点关注全时间序列聚类。
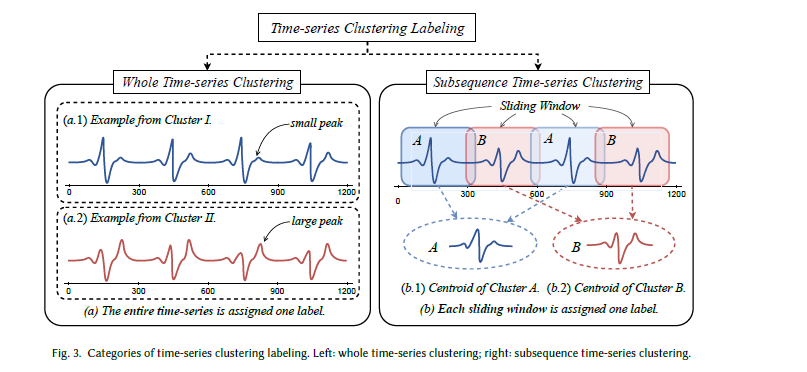
在这里插入图片描述

图3 时间序列聚类标记类别。左：全时间序列聚类；右：子序列聚类。

根据每个时间步的贡献方式，全时间序列聚类可分为两类（如图4所示）：图4（a）展示了将所有时间步同等对待的传统聚类过程；图4（b）展示了以一组子序列为指导的基于子序列的全时间序列聚类。需注意的是，后者与前文所述的子序列聚类不同，其最终仍会为整个时间序列生成聚类标签。
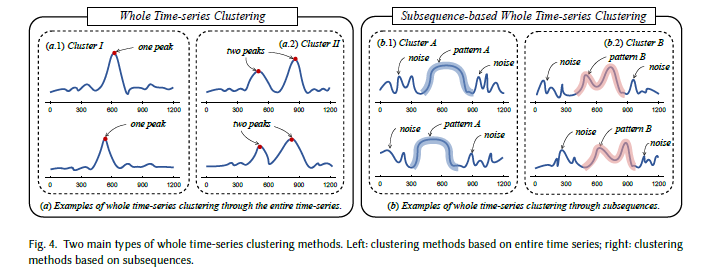
在这里插入图片描述

图4 全时间序列聚类的两种主要类型。左：基于完整时间序列的聚类方法；右：基于子序列的全时间序列聚类方法。

2.3 时间序列聚类流程

在深入探讨具体聚类算法之前，了解时间序列聚类的通用流程至关重要。基于以往研究[3, 7, 143]的见解，本文将时间序列聚类的通用流程总结为三个部分（如图5所示）：表示、相异度度量和聚类过程。这种分解不仅有助于对各类时间序列聚类算法进行比较评估，还能帮助揭示时间序列聚类的本质，为新型算法的研发提供支持。

2.3.1 表示

表示过程（又称数据表示或特征提取）是指将时间序列转换为便于下游任务处理的数据格式。原始时间序列数据是基础格式，包含自然信号中的丰富特征信息，被广泛应用于各类聚类算法中。然而，信号记录过程中的噪声干扰为寻找有意义的模式带来了挑战，且原始空间的高维度也大幅增加了数据分析的时间和成本。因此，提取有意义特征同时保留关键信息的有效方法具有重要意义。时间序列表示的定义如下：

定义2.5：给定包含 $T$ 个时间步的时间序列数据 $x_i = \{x_{i1}, x_{i2}, ..., x_{iT}\}$ ，需找到一个变换 $\phi: x_i \to x_i'$ ，其中 $x_i' = \{x_{i1}', x_{i2}', ..., x_{iK}'\}$ 表示新的表示形式（在降维场景中，通常满足 $K < T$ ）。变换空间需保留原始空间的关键信息，即若 $x_i$ 与 $y_i$ 相似，则 $x_i'$ 与 $y_i'$ 也应相似，反之亦然。

如图5所示，时间序列表示主要分为数值型和符号型两类。数值型时间序列表示采用实值数组（单变量）或矩阵（多变量）来表示原始信号中的特征信息，通常具有较低的维度，代表性技术包括离散傅里叶变换（DFT）[6, 60, 113]、离散小波变换（DWT）[6, 37, 113]、分段线性近似（PLA）[117]、分段聚合近似（PAA）[118, 255]，以及深度学习兴起后出现的神经网络方法[29, 71, 83, 162, 256, 258]。另一方面，符号型时间序列表示[144, 164, 208]兼具降维和文本方法（如哈希、序列匹配）的优势，代表性方法包括符号聚合近似（SAX）[116, 145]、可索引符号聚合近似（iSAX）[145]、符号傅里叶近似（SFA）[208]和1d-SAX[164]。如图5所示，符号型表示的输入既可以是原始时间序列数据，也可以是经过变换后的表示形式。

2.3.2 相异度度量

由定义2.4可知，时间序列聚类的核心目标是对数据进行划分，使具有相同模式的时间序列归为一类。为从数学角度解决这一问题，研究者提出了相异度度量（又称距离度量），用于量化两个序列（可为原始数据或变换后的表示）之间的接近程度或分离程度。根据定义，完全相同的时间序列之间的相异度度量值应为0，而属于不同簇的时间序列之间的相异度度量值应足够大。通过不同的设计，相异度度量可捕捉时间、形状和结构方面的相似性信息[3]。通常，相异度度量主要分为三类：同步度量（lock-step measure）、弹性度量（elastic measure）和滑动度量（sliding measure），图5对各类度量进行了概述。

这三类相异度度量各有优缺点：一方面，同步度量的一对一映射假设简化了不同时间序列间的比较过程，时间复杂度较低（接近 $O (n)$ ，其中 $n$ 为序列长度）；但另一方面，欧氏距离等相异度度量对变长时间序列数据存在局限性，且一对一映射易受自然信号中固有噪声的干扰。相反，弹性度量可对不同区域进行灵活对齐，对各类干扰具有鲁棒性，在多种时间序列分析任务中取得了良好效果。然而，文献[182]的研究表明，多数弹性度量在基准数据集上的性能并不显著优于滑动度量，且两者在时间消耗上存在较大差距。换言之，在不同场景下，滑动度量可在运行时间和准确性之间取得良好平衡。

同步度量：聚焦于两条完整时间序列的一对一映射，最终结果通常通过计算每个时间点误差的总和或平均值得到。代表性方法包括欧氏距离（ED）[60, 73]、闵可夫斯基距离（即 $L_p$ 范数）[19, 73, 182]、洛伦兹距离（即 $L_1$ 范数的自然对数）[73, 182]、曼哈顿距离[73, 182]和杰卡德距离[73, 182]。
弹性度量：常用于一对一映射假设不成立的场景。由于噪声干扰和信号本身的特性，两条时间序列数据样本可能具有相似性，但在幅度（缩放）和偏移（平移）方面存在差异，此时同步度量的性能易下降甚至失效。为解决这一问题，弹性度量方法通过“弹性”方式构建一对多/多对一映射，实现对不同区域时间点的灵活对齐[182]。代表性弹性度量包括动态时间规整（DTW）[25, 46, 198, 207]、最长公共子序列（LCSS）[10, 233]、移动-分割-合并（MSM）[89, 215]。
滑动度量：另一类相异度度量，通过滑动机制实现不同序列的全局对齐。代表性滑动度量包括归一化互相关（NCC）的变体，如基于形状的距离（SBD）[178]。借助快速傅里叶变换（FFT）的优势，其计算成本可降至 $O(n\log n)$ ，相较于原始DTW（时间复杂度 $O(n^2)$ ）实现了显著的速度提升[182]。

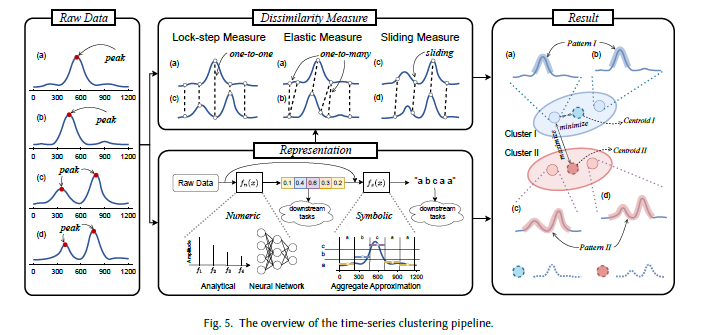
图5 时间序列聚类流程概述

3 时间序列聚类分类体系

本节将时间序列聚类算法（包括传统方法和深度学习方法）分为四类：（1）基于距离的方法；（2）基于分布的方法；（3）基于子序列的方法；（4）基于表示学习的方法，并提出相应的分类体系。图6展示了该分类体系及各类别的示意图，下文将详细阐述各类别的定义。
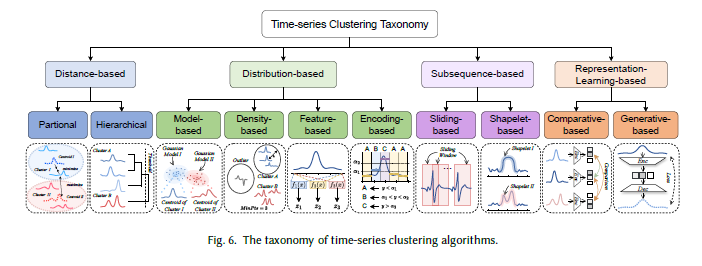
在这里插入图片描述

图6 时间序列聚类算法分类体系

3.1 基于距离的方法

顾名思义，基于距离的方法的核心思想是度量两条原始时间序列 $X_A$ 和 $X_B$ 之间的距离 $D i s t$ ，其中若两条时间序列完全相同，则 $Dist(X_A, X_B) = 0$ 。欧氏距离（ED）作为多种数据格式中最常用的距离度量之一，已在多个研究领域取得成功。然而，由于其同步设计特性，这种高效的距离度量通常难以处理时间序列数据中的固有差异（如缩放差异、偏移差异、遮挡差异等）。为解决这一问题，研究者提出了多种专为时间序列数据设计的距离度量方法，如动态时间规整（DTW）和基于形状的距离（SBD）。

通过计算每对时间序列之间的距离，若 $Dist(X_A, X_B)$ 较小，则可将 $X_A$ 和 $X_B$ 归为一类，反之则归为不同类。为对每条时间序列做出合理分类，基于距离的方法可进一步分为两类：划分式模型和层次式模型，详见第4章。

划分式聚类算法：将 $N$ 条无标签时间序列划分为 $K$ 个带有质心的簇，每条时间序列与所属簇质心的距离最小。在训练过程中，通常通过迭代优化簇质心和样本分配。
层次式聚类算法：通过构建簇的层次结构对对象进行分组。根据层次结构的不同，可分为凝聚式（agglomerative）和分裂式（divisive）两类：凝聚式方法从每条时间序列单独作为一个簇开始，逐步将小簇合并为大簇，直至满足特定条件；分裂式方法则从所有时间序列归为一个簇开始，逐步将其拆分，直至满足特定条件。

3.2 基于分布的方法

基于分布的聚类聚焦于对时间序列数据的分布进行建模，为确定簇间边界提供指导。需注意的是，此处的“分布”是广义概念，既包括显式分布（如数据点的密度），也包括隐式分布（如使用预训练字典对时间序列进行编码）。基于分布的方法可进一步分为四类：基于模型的方法、基于密度的方法、基于特征的方法和基于编码的方法，详见第5章。

基于模型的聚类方法：通过可学习参数对时间序列数据的显式分布进行建模，如高斯混合模型（GMM）和隐马尔可夫模型（HMM）。每条时间序列可通过一组参数进行建模和表示，这些参数可为后续时间序列聚类提供指导。
基于密度的聚类方法：将簇定义为对象密集分布的区域，簇边界通常位于稀疏或空无数据的区域。例如，这类方法在密集邻域中扩展簇，并在数据点变得稀疏的位置建立边界。
基于特征的时间序列聚类方法：通过全局描述性特征来表示时间序列的特征。考虑到时间序列数据模态中的固有差异，噪声干扰可能会给样本间的距离度量带来挑战。为解决这一问题，描述性特征可作为鲁棒的噪声表示用于聚类。
基于编码的时间序列聚类方法：构建原始空间与变换空间（又称latent空间）之间的映射函数 $\to Z$ ，其中latent表示 $z$ 包含原始数据的关键特征信息。当变换空间的维度小于原始空间时，该过程通常被视为降维技术。

3.3 基于子序列的方法

如2.2节所定义，基于子序列的聚类是全时间序列聚类中的一种特殊情况。在此过程中，从完整时间序列中提取代表性子序列，将其作为聚类的有效模式。由于考虑所有时间步时，噪声干扰可能导致性能下降，因此通过选择描述性子序列，模型可在不同场景下规避这一问题。基于子序列的方法可进一步分为两类：基于滑动窗口的方法和基于形状子（shapelet）的方法，详见第6章。

基于滑动窗口的方法：通过滑动窗口获取一组子序列。在某些情况下，这些子序列可视为原始时间序列的片段，用于从较低层级度量距离；而其他模型则将子序列信息作为先验知识，用于多阶段聚类。
基于形状子的方法：聚焦于可作为原始时间序列有意义模式的子序列（又称形状子[253]）。根据目标不同，以往研究要么通过迭代搜索特定子序列，要么直接从数据集中学习形状子。

3.4 基于表示学习的方法

与前文所述的基于特征或基于编码的方法类似，基于表示学习的方法也致力于为原始时间序列数据设计新的表示形式。然而，前两类方法需要显式数学公式计算数值，而基于表示学习的方法通过学习过程获取表示。这种新表示可作为k-Means[161]等简单聚类模型的输入。随着深度神经网络和无监督学习策略的发展，基于表示学习的算法在多个任务中取得了显著成功。根据学习策略的特征，可将其分为两类：基于比较的方法和基于生成的方法，详见第7章。

基于比较的时间序列聚类方法：通过比较方式（如比较相似/不相似的时间序列样本）学习编码映射函数 $\varepsilon: X \to Z$ 。编码映射函数可通过神经网络学习，下文将详细阐述。
基于生成的时间序列聚类方法：与基于比较的聚类方法不同，这类方法通过对生成输出施加约束来学习鲁棒表示。例如，重构任务：通过重构方式联合学习编码映射函数 $\varepsilon: X \to Z$ 和解码映射函数 $\to X$ ，深度神经网络能够找到数据表示的优良latent空间，且该空间的维度可能更低。

4 基于距离的方法

本章探讨基于距离的聚类方法，这类方法完全依赖数据间、簇间或两者兼具的相异度度量，将相似元素归为一类。该类方法通常无需特定的数据表示或特征选择，仅通过原始时间序列即可生成有意义的输出。基于距离的方法可进一步分为两类：划分式方法和层次式方法。划分式方法将 $n$ 条无标签时间序列划分为 $k$ 个簇，并确保每个簇至少包含一条时间序列；层次式方法则通过构建层次结构对数据进行分组。下文将在4.1节和4.2节中详细探讨这两类方法的概念和代表性算法。

4.1 划分式聚类

划分式聚类算法将 $n$ 条无标签时间序列划分为 $k$ 个簇，并确保每个簇至少包含一条时间序列。此外，如图7所示，划分式聚类方法可分为两类：硬划分方法和模糊划分方法。在硬划分方法中，每个数据点仅属于一个簇；而在模糊划分方法中，每个数据点与多个簇存在隶属概率，可同时属于多个簇。下文将分别详细探讨这两类方法的代表性算法，相关方法汇总于表1。

表1 划分式聚类方法汇总

方法名称	距离度量	原型（Prototype）	维度（Dim）
k-Means [161]	欧氏距离（ED）	k-Means	多变量（M）
k-Medoids [199]	任意（*）	k-Medoids	单变量（I）
k-Medians [100]	曼哈顿距离	k-Medians	单变量（I）
M-RC [123]	欧氏距离（ED）	k-Medoids	多变量（M）
CB-FCM [75]	基于互相关（CC-based）	模糊C均值（FCM）	单变量（I）
NTSA-TC [192]	欧氏距离（ED）	模糊C均值（FCM）	单变量（I）
M-k-Medoids [142]	动态时间规整（DTW）	k-Medoids	单变量（I）
FSTS [170]	STS距离	模糊C均值（FCM）	单变量（I）
k-DBA [190]	动态时间规整（DTW）	k-DBA	单变量（I）
K-SC [250]	STI距离	K-SC	单变量（I）
DFC [103]	欧氏距离（ED）	模糊C均值（FCM）	单变量（I）
DKM-S [209]	任意	k-Median	多变量（M）
k-Shape [178]	基于形状的距离（SBD）	k-Shape	单变量（I）
k-MS [179]	基于形状的距离（SBD）	k-MS	单变量（I）
m-kAVG [173]	m-ED	k-Means	多变量（M）
m-kDBA [173]	m-DTW	k-DBA	多变量（M）
m-kSC [173]	m-STI	K-SC	多变量（M）
m-kShape [173]	m-SBD	k-Shape	多变量（M）

注：I：单变量；M：多变量；*：任意。

4.1.1 硬划分方法

k-Means[161]是应用最广泛的划分式聚类算法之一。给定质心数量 $k$ ，k-Means首先随机选择 $k$ 条时间序列作为初始质心；随后，通过欧氏距离（ED）计算每个对象与所有质心的距离，将每个对象分配到质心距离最近的簇中，并将每个簇的质心更新为该簇内所有对象的均值；重复上述过程，直至满足预设收敛条件。然而，k-Means对质心初始化敏感，文献[13]提出k-Means++算法以改进k-Means性能：通过定义质心初始化规则，基于对象与已选最近质心的距离概率迭代添加新质心，使初始质心尽可能分散。

k-Means的一种变体是k-Medians[100]。与k-Means不同，k-Medians不使用欧氏距离作为度量且不将簇均值作为质心，而是采用曼哈顿距离作为度量，并将簇中位数作为质心。

另一类重要的聚类算法是k-Medoids[112]，其目标同样是最小化簇内数据点与簇质心的距离。但与k-Means不同，k-Medoids可使用任意距离度量，且以数据集中实际存在的、最具代表性的数据点（即中心点，medoid）作为质心。也就是说，中心点是簇内的一个实际数据点，其与簇内其他所有点的平均距离最小。围绕中心点的划分（PAM）[112]是k-Medoids聚类算法家族中最经典、最具代表性的方法之一。与k-Means不同，PAM通过“PAM Swap”算法更新质心：对于每个中心点 $m$ ，PAM Swap将其与非中心点 $o$ 交换，重新分配数据点并计算聚类总成本；若总成本降低，则保留交换并重复该过程；否则，撤销最后一次交换并终止。与k-Means相比，以中心点作为质心增强了算法对异常值的鲁棒性，并提升了质心的可解释性。但与k-Means类似，k-Medoids聚类算法也需要输入簇数量。

此外，k-Means的另一种扩展变体是k-DBA[190]，它采用动态时间规整（DTW）[207]作为距离度量，并将DTW重心平均（DBA）方法用于质心计算。在每次迭代优化中，DBA通过计算平均序列与其他每条序列的DTW，获取相关坐标的重心，进而更新平均序列的每个坐标。K-谱重心（K-SC）[250]聚类算法是对k-Means的改进，它采用缩放和平移不变（STI）距离度量以及矩阵分解技术来更新质心。

k-Shape[178]是该类别中的另一种算法，也是当前最先进的时间序列聚类算法之一。与k-Means不同，k-Shape采用SBD作为距离度量。通过采用归一化互相关并在频域加速计算，SBD相较于DTW等其他高性能算法，成本更低、效率更高。在质心计算方面，k-Shape基于SBD将同一簇内的对象与簇质心对齐；由于互相关可捕捉相似性，目标函数转化为寻找新质心以最大化簇内平方相似性总和。随后，该优化问题可转化为瑞利商（Rayleigh Quotient）[76]的最大化问题，新质心即为与最大特征值相关联的特征向量。

4.1.2 模糊划分方法

除了将 $n$ 个对象以硬划分方式归为 $k$ 个簇（强制每个对象仅属于一个簇）外，模糊划分算法允许一个对象在一定程度上属于多个簇。该类别中最具代表性的算法之一是模糊C均值（FCM）[51, 26]。在FCM中，每个数据点对每个簇都有一个模糊隶属度值，这些隶属度值为0-1之间的实数，表示数据点属于特定簇的可能性大小。此外，对于每个数据 $x_i$ 和簇 $c_j$ ，FCM计算 $x_i$ 与簇质心 $c_j$ 的距离，并通过 $x_i$ 对 $c_j$ 的隶属度对该距离进行加权。FCM的目标是最小化所有数据-簇对的加权距离总和，通过迭代更新隶属度值和簇质心直至收敛；收敛后，基于最终隶属度值确定聚类结果。

文献[75]将FCM应用于功能磁共振成像（fMRI）数据，并探讨了其在三个参数上的优化可能性：（1）数据集预处理方法；（2）距离度量；（3）簇数量。由于研究者期望基于相似性对像素时间序列进行聚类，因此提出了两种基于互相关（CC-based）的距离度量，并将其与欧氏距离（ED）进行比较，以寻找最优度量。

考虑到现实场景中常存在短时间序列（STS）和非均匀采样时间序列的问题，并受分子生物学领域观察结果的启发，文献[170]提出了一种改进的模糊聚类方案：将新提出的STS距离（可同时捕捉幅度相对变化形成的形状相似性和相应时间信息）应用于标准模糊聚类算法中。
在这里插入图片描述

图7 划分式时间序列聚类概述。图中两个表格分别表示硬划分和模糊划分方法下的分配概率。

4.2 层次式聚类

层次式聚类通过构建簇的层次结构对对象进行分组，在时间序列聚类中具有良好的可视化能力。层次式聚类方法可分为两类：凝聚式和分裂式。凝聚式层次（AH）聚类算法从每条时间序列单独作为一个簇开始，逐步将小簇合并为大簇，直至满足特定条件；分裂式层次（DH）聚类算法则从所有时间序列归为一个簇开始，逐步将其拆分，直至满足特定条件。相关方法汇总于表2。

表2 层次式聚类方法汇总

方法名称	链接方式（Linkage）	距离度量	维度（Dim）
DC-MTS [109]	凝聚式（AH）+ 无指定（/）	KL距离 + 切尔诺夫距离	多变量（M）
TSC-CBV [230]	凝聚式（AH）+ 无指定（/）	均方根（Root mean square）	单变量（I）
local-clustering [193]	凝聚式（AH）+ 单链接（single）	自定义距离（Ad hoc distance）	单变量（I）
hError [128]	凝聚式（AH）+ 误差调整（error-adjusted）	误差高斯模型（Gaussian models of errors）	单变量（I）
TFDC [213]	凝聚式（AH）+ 无指定（/）	KL距离	多变量（M）
ODAC [201]	分裂式（DH）+ 凝聚式（AH）+ 准则（criteria）	RNOMC	多变量（M）
TSC-CN [263]	凝聚式（AH）+ 平均链接（average）	三角相似性 + DTW	单变量（I）
TSC-PDDTW [155]	凝聚式（AH）+ 平均链接（average）	DTW + DDTW	单变量（I）
HSM [59]	凝聚式（AH）+ 谱基于（spectral-based）	总变差距离（Total variation distance）	单变量（I）
TSC-BD [221]	凝聚式（AH）+ 全链接（complete）	DTW	单变量（I）
TSC-COVID [157]	凝聚式（AH）+ 沃德链接（Ward’s）	DTW	单变量（I）

注：I：单变量；M：多变量；/：无指定。

在凝聚式层次（AH）聚类中，由于所有合并操作均在簇级别进行，且每个簇至少包含一个对象，因此需要引入簇间的相似性或相异度度量，簇间距离的度量和表示成为重要研究方向。为此，本文列出了层次式聚类中常用的几种链接方式[112]，用于度量簇间距离：

单链接（single linkage）：给定两条时间序列的簇 $C_i$ 和 $C_j$ ，首先计算所有成对距离 $\{dist(x, y) | \forall x \in C_i, \forall y \in C_j\}$ （其中 $d i s t (x, y)$ 是用于度量两条时间序列 $x$ 和 $y$ 的距离函数），则 $C_i$ 和 $C_j$ 之间的距离定义为 $D$ 中的最短距离。
全链接（complete linkage）：给定簇 $C_i$ 和 $C_j$ ，按单链接的方式计算所有成对距离 $D$ ，则 $C_i$ 和 $C_j$ 之间的距离定义为 $D$ 中的最长距离。
平均链接（average linkage）：给定簇 $C_i$ 和 $C_j$ ，按上述方式计算所有成对距离 $D$ ，则 $C_i$ 和 $C_j$ 之间的距离定义为 $D$ 的平均值。
质心链接（centroid linkage）：给定簇 $C_i$ 和 $C_j$ ，首先计算每个簇的质心（均值时间序列），分别记为 $C_i$ 的 $\overline{C_i}$ 和 $C_j$ 的 $\overline{C_j}$ ，则两簇之间的距离表示为 $dist(\overline{C_i}, \overline{C_j})$ 。
沃德链接（Ward’s linkage）[237]：给定簇 $C_i$ 和 $C_j$ ，两簇之间的距离 $\Delta(C_i, C_j)$ 定义为合并后簇内总方差的增加量。

值得注意的是，尽管多数研究采用不同链接方式的凝聚式层次聚类方法，但文献[201]提出了一种名为在线分裂-凝聚聚类（ODAC）的系统，该系统结合分裂式层次（DH）和凝聚阶段对时间序列数据流进行聚类。ODAC采用分裂式层次方法，以根归一化1-相关（RNOMC）作为相异度度量，并基于最不相似的流对拆分节点；此外，它还引入凝聚阶段以重新合并先前拆分的节点，从而适应时间序列间相关结构的变化。

与划分式聚类算法相比，层次式聚类算法无需预先定义簇数量；且文献[143]指出，若采用合适的距离度量，层次式聚类可对变长时间序列进行聚类。然而，层次式聚类算法一旦开始，难以调整已形成的簇，因此在聚类质量和性能上有时表现较弱。此外，文献[3]指出，层次式聚类的计算复杂度为二次级，因此由于计算复杂度高、可扩展性差，不适用于大规模数据集。

5 基于分布的方法

本章探讨基于分布的聚类方法，这类方法根据时间序列数据的显式或隐式分布对其进行分组。与基于距离的聚类方法不同，基于分布的聚类方法强调对时间序列数据分布的提取、选择、学习和利用。基于分布的聚类方法可进一步分为四类：基于模型的方法（5.1节）、基于密度的方法（5.2节）、基于特征的方法（5.3节）和基于编码的方法（5.4节）。下文将为每类方法提供精确定义，并阐述代表性算法。

5.1 基于模型的方法

基于模型的聚类方法通过一组参数对时间序列数据的潜在分布进行建模。由此，两条时间序列之间的距离可转化为两组参数的比较。代表性建模技术包括高斯混合模型（GMM）、隐马尔可夫模型（HMM）、自回归移动平均模型（ARMA）和积分自回归移动平均模型（ARIMA）。相关方法汇总于表3。

5.1.1 高斯混合模型（GMM）

GMM[28]是一种概率模型，通过多个高斯分布的混合来近似数据集。假设给定簇数量 $K$ ， $K$ 个多变量高斯分布的混合函数如下：

$\mathcal{N}(x_i | \mu_j, \sum_j) = \frac{1}{(2\pi)^{D/2}|\sum_j|^{1/2}} \exp\left(-\frac{1}{2}(x_i - \mu_j)^T \sum_j^{-1}(x_i - \mu_j)\right)$

$p(x_i) = \sum_{j=1}^K \pi_j \cdot \mathcal{N}(x_i | \mu_j, \sum_j)$

其中， $N(x_i | \mu_j, \sum_j)$ 表示参数未知（ $\mu_j, \sum_j$ ）的多变量高斯密度函数， $D$ 表示数据维度；对于第 $j$ 个簇， $\mu_j$ 为均值， $\sum_j$ 为协方差矩阵， $\pi_j$ 为混合比例。为估计这些参数，可通过最大化完整对数似然（具有闭式最大值）实现。然而，完整对数似然需要观测每个 $x_i$ 的簇分配 $z_i$ （这些分配未知且需学习），因此在GMM的学习阶段，采用期望最大化（EM）算法：从随机初始化开始，迭代执行期望步（E-step）和最大化步（M-step），直至收敛。

在E-step中，计算如下模糊类隶属度：

$\gamma_{ij} = \frac{\pi_j \cdot \mathcal{N}(x_i | \mu_j, \sum_j)}{\sum_{k=1}^K \pi_k \cdot \mathcal{N}(x_i | \mu_k, \sum_k)} \tag{3}$

在M-step中，参数的闭式最大值解由以下公式给出：

$\pi_j = \frac{1}{N} \sum_{i=1}^N \gamma_{ij} \tag{4}$

$\mu_j = \frac{\sum_{i=1}^N \gamma_{ij} x_i}{\sum_{i=1}^N \gamma_{ij}} \tag{5}$

$\sum_j = \frac{\sum_{i=1}^N \gamma_{ij}(x_i - \mu_j)(x_i - \mu_j)^T}{\sum_{i=1}^N \gamma_{ij}} \tag{6}$

其中 $N$ 为数据数量。模型训练完成后，对于新数据点，可基于学习到的参数计算其属于每个簇的概率，并将其分配到概率最高的簇中。

5.1.2 隐马尔可夫模型（HMM）

HMM[28]是一种概率图模型，旨在基于观测数据推断潜在的隐藏状态及状态间的转移关系，图8展示了HMM的一个示例。HMM基于两个核心假设：给定状态空间 $\{s_1, s_2, \cdots, s_N\}$ 和观测空间 $\{o_1, o_2, \cdots, o_V\}$ ，设 $n$ 个隐藏状态序列为 $\{x_1, x_2, \cdots, x_n\}$ ， $n$ 个观测序列为 $\{y_1, y_2, \cdots, y_n\}$ ，则下一个状态 $x_{i+1}$ 和当前观测仅依赖于当前状态 $x_i$ 。

在HMM中，除初始概率外，存在两类概率：转移概率和发射概率。转移概率表示从一个隐藏状态转移到另一个隐藏状态的可能性；发射概率表示在当前隐藏状态下生成特定观测的概率。此外，转移矩阵 $\in \mathbb{R}^{N \times N}$ 包含隐藏状态间的转移概率，发射矩阵 $\in \mathbb{R}^{N \times V}$ 包含从隐藏状态到观测的发射概率。

为估计HMM的参数，通常需寻找：

$\mathcal{T}^*, Q^* = \arg\max_{\mathcal{T}, Q} P(Y | \mathcal{T}, Q) \tag{7}$

HMM的学习同样采用EM算法，其中最著名的HMM-EM算法实例是鲍姆-韦尔奇（Baum-Welch）算法[20]。通过训练好的HMM，对于新数据，可推断生成该观测的最可能隐藏状态序列，并基于推断出的隐藏状态相似性进行聚类。
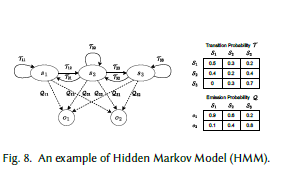
在这里插入图片描述

图8 隐马尔可夫模型（HMM）示例

5.1.3 自回归模型（AR）

AR[95]是一种统计模型，认为时间序列的未来值受其历史值影响。该模型通过预定义数量的历史值（即AR的阶数）的线性组合来预测时间序列的值，阶数为 $p$ 的AR模型可表示为：

$x_t = \sum_{j=1}^p \phi_j x_{t-j} + \varepsilon_t + c$

其中，在时间序列 $x$ 中， $x_t$ 表示时间步 $t$ 的当前值， $\phi_j$ 是与时间步 $t - j$ 的历史值相关联的系数， $\varepsilon_t$ 是时间步 $t$ 的误差项， $c$ 是常数项。

5.1.4 移动平均模型（MA）

MA[95]是另一种经典统计模型，将时间序列的当前值与历史误差相关联。给定MA的阶数 $q$ ，MA通过时间序列的均值 $\mu$ 与历史误差的线性组合来计算时间步 $t$ 的序列值，公式如下：

$x_t = \sum_{j=1}^q \theta_j \varepsilon_{t-j} + \varepsilon_t + \mu$

其中，在时间序列 $x$ 中， $x_t$ 表示时间步 $t$ 的值， $\theta_j$ 是与时间步 $t - j$ 的误差 $\varepsilon_{t-j}$ 相关联的参数， $\varepsilon_t$ 是时间步 $t$ 的误差项。

将阶数为 $p$ 的AR模型与阶数为 $q$ 的MA模型结合，可得到时间序列分析模型——自回归移动平均（ARMA）模型[95]，该模型基于历史值和误差项对时间序列的当前值进行表征。ARIMA[95]是对ARMA的扩展，它将差分操作与ARMA结合，使其能够处理时间序列数据的非平稳性。

表3 基于模型的聚类方法汇总

方法名称	聚类方式	模型	距离度量	维度（Dim）
TSC-ARIMA-ED [191]	凝聚式+全链接	ARIMA	欧氏距离（ED）	单变量（I）
TSC-HISMOOTH [24]	凝聚式+无指定	HISMOOTH	无指定（/）	单变量（I）
TSC-D-HMM [133]	4级搜索	HMM	对数似然（Log-likelihood）	多变量（M）
TSC-HMM-DTW [171]	混合式	离散HMM	DTW	多变量（M）
ICL [27]	TSC-ICL	GMM	对数似然（Log-likelihood）	多变量（M）
TSC-AR-HT [163]	凝聚式+基于检验	AR	假设检验（Hypothesis test）	单变量（I）
MBCD [194]	凝聚式+基于概率	马尔可夫链	KL距离	多变量（M）
TSC-LPC-ARIMA [110]	PAM	ARIMA	欧氏距离（ED）	单变量（I）
BHMMC [134]	4级搜索	HMM	贝叶斯信息准则（BIC）	多变量（M）
FCM-SV [227]	改进FCM	GMM	对数似然（Log-likelihood）	单变量（I）
TSC-ARMAM [245]	基于概率	ARMAs	对数似然（Log-likelihood）	单变量（I）
R-TS-BHC [47]	贝叶斯层次聚类	高斯过程	狄利克雷过程（Dirichlet process）	单变量（I）
TSC-HMM-S-KL [72]	PAM	HMM	S-KL散度	多变量（M）

注：I：单变量；M：多变量；/：无指定。

5.2 基于密度的方法

在基于密度的聚类中，簇是对象密集分布的子空间，这些密集区域被空或稀疏区域分隔。与基于模型的聚类方法不同，基于密度的聚类技术利用时间序列数据的显式分布。值得注意的是，许多基于密度的聚类方法可直接应用于原始时间序列数据，无需特定的数据表示。下文将探讨该类别中一些著名的经典方法，更多相关方法汇总于表4。

表4 基于密度的聚类方法汇总

方法名称	表示形式	距离度量	维度（Dim）
DBSCAN [58]	原始数据	欧氏距离（ED）	多变量（M）
DENCLUE [87]	基于映射	高斯核（Gaussian kernel）	多变量（M）
OPTICS [11]	原始数据	欧氏距离（ED）	多变量（M）
FDBSCAN [125]	模糊对象	模糊距离（Fuzzy distance）	多变量（M）
DENCLUE 2.0 [86]	原始数据	高斯核（Gaussian kernel）	多变量（M）
D-Stream [41]	原始数据	密度函数（Density function）	多变量（M）
DPC [202]	原始数据	欧氏距离（ED）	多变量（M）
TADPole [23]	原始数据	约束DTW（cDTW）	多变量（M）
YADING [50]	原始数据	L1距离	单变量（I）
ADBSCAN [119]	原始数据	欧氏距离（ED）	多变量（M）

注：I：单变量；M：多变量。

5.2.1 基于密度的带噪声应用空间聚类（DBSCAN）[58]

DBSCAN通过在密集邻域中扩展簇来形成聚类。给定以对象为中心的圆形邻域半径 $\varepsilon$ 和最小密度阈值MinPts，DBSCAN首先将核心点（圆形邻域内至少包含MinPts个对象的对象）与非核心点区分开；随后，随机选择一个未分组的核心点，通过迭代添加与当前簇中任何核心点距离在 $\varepsilon$ 内的新核心点来扩展簇，直至无法添加更多核心点；此外，新簇还包含与簇内任何核心点距离在 $\varepsilon$ 内的所有非核心点；最后，重复上述步骤（除第一步外）以形成其余簇，直至所有核心点均属于某个簇。

DBSCAN的优势主要体现在以下方面：（1）无需用户确定簇数量和形状参数；（2）可处理大规模数据集；（3）对异常值和噪声具有鲁棒性。

5.2.2 有序点识别聚类结构（OPTICS）[11]

与生成显式聚类不同，OPTICS生成对象的增强排序，并生成称为“可达性图”的可视化表示，以反映对象的基于密度的聚类结构。作为DBSCAN的扩展，OPTICS引入了两个额外术语：

核心距离（core-distance）：对象 $p$ 的核心距离计算公式如下：
$core\text{-}dist(p) = \begin{cases} \varepsilon', & \text{若} \ p \ \text{是核心点} \\ \text{未定义（Undefined）}, & \text{否则} \end{cases}$
其中 $\varepsilon'$ 表示将 $p$ 分类为核心点所需的最小距离。
可达距离（reachability-distance）：对象 $p$ 相对于对象 $q$ 的可达距离定义为：
$reachability\text{-}dist(p, q) = \begin{cases} \max(core\text{-}dist(q), dist(q, p)), & \text{若} \ q \ \text{是核心点} \\ \text{未定义（Undefined）}, & \text{否则} \end{cases}$
其中 $d i s t (q, p)$ 表示对象 $q$ 与对象 $p$ 之间的距离，默认采用欧氏距离。

与DBSCAN相比，OPTICS具有多项优势，例如可在不同密度级别提取簇，且对参数的敏感性更低。

5.2.3 基于密度的聚类（DENCLUE）[87]

DENCLUE是一种比DBSCAN更高效的算法，它通过基于欧氏距离的高斯影响函数对每个对象的影响进行建模，描述对象在其邻域内的影响。通过基于映射的表示，DENCLUE仅考虑高人口密度立方体及其相连的立方体，从而加速聚类步骤。为提高执行效率，DENCLUE不计算数据空间的整体密度（定义为所有对象影响函数的总和），而是计算局部密度函数——通过仅考虑邻近点的影响来近似整体密度函数。随后，通过爬山法可获得密度吸引子（密度函数的局部最大值）。得益于坚实的数学基础，DENCLUE除了对噪声具有不变性外，在大规模高维数据上也具有高效性，且适用于寻找各种形状的簇。

5.2.4 密度峰值聚类（DPC）[202]

DPC是该类别中另一种值得关注的代表性算法，其核心思想是：簇中心的密度高于其邻居，且与密度更高的点保持较大距离。对于每个对象 $i$ ，DPC通过以下公式计算局部密度 $\rho_i$ 和相对距离 $\delta_i$ ，并绘制决策图：

$\rho_i = \sum_j \chi(dist(i, j) - dist_c) \tag{12}$

$\chi(x) = \begin{cases} 1, & \text{若} \ x < 0 \\ 0, & \text{否则} \end{cases}$

$\delta_i = \begin{cases} \max_j(dist(i, j)), & \text{若} \ i \ \text{是密度最高的点} \\ \min_{j: \rho_j > \rho_i}(dist(i, j)), & \text{否则} \end{cases}$

其中 $d i s t (i, j)$ 表示对象 $i$ 与对象 $j$ 之间的距离， $dist_c$ 表示截断距离。计算完 $\rho_i$ 和 $\delta_i$ 后，DPC为数据集中的每个对象 $i$ 构建决策图：以 $\rho$ 为x轴， $\delta$ 为y轴，将 $\rho$ 和 $\delta$ 值均较高的对象定义为簇中心。确定簇中心后，DPC将每个剩余点分配到密度更高的最近邻居所属的簇中。

为区分异常值，DPC为每个簇识别边界区域（属于该簇且与其他簇对象距离在 $dist_c$ 内的对象集合）；在每个簇的边界区域中，识别局部密度最高的对象 $b$ 并记录 $\rho_b$ ；通过将簇内每个对象的局部密度与 $\rho_b$ 比较，将局部密度小于 $\rho_b$ 的对象视为异常值。

5.2.5 时间序列任意时间密度峰值（TADPole）[23]

TADPole是DPC的变体，采用cDTW作为距离度量。与DPC相比，TADPole需要额外的上界和下界矩阵；正如作者所述，空间复杂度并非问题，因为DPC的瓶颈在于CPU，且将下界矩阵编码为稀疏矩阵可减少空间开销。在局部密度计算中，TADPole基于四种情况修剪距离计算；同时，在计算每个对象到密度更高的最近邻居的距离时，采用两阶段修剪策略。文章指出，单变量TADPole只需少量修改即可扩展到多变量场景。

5.3 基于特征的方法

时间序列作为基础数据格式之一，表征了信号值随时间的变化。然而，如前所述，噪声干扰会给寻找有意义信息带来挑战，尤其是在维度极高的情况下。为解决这一问题，基于特征的时间序列聚类方法通过全局描述性特征来表征时间序列的特征。下文将详细探讨代表性方法，更多相关方法汇总于表5。

5.3.1 基于特征的聚类（CBC）[234]

鉴于长时序列和缺失数据可能导致许多现有聚类算法失效，研究者提出了CBC。CBC利用全局结构特征度量（结合经典统计度量和先进特殊度量）对时间序列进行聚类，这些特征包括趋势、季节性、周期性、序列相关性、偏度、峰度、混沌性、非线性和自相似性。借助这些全局表示，CBC可显著降低时间序列数据的维度，并对缺失或噪声数据表现出更强的鲁棒性。在聚类方法方面，为获得良好的可视化效果，CBC作者仅通过层次式聚类和自组织映射（SOM）进行实验。此外，作者指出，合适的特征集不仅能提高计算效率，还能生成更优的聚类结果，因此设计了一种基于贪心前向搜索（FS）的新技术，用于选择优化的特征子集。

5.3.2 tsfresh [44]

由于时间序列特征工程需要浏览大量信号处理和时间序列分析算法以提取合适的有意义特征，过程耗时，因此研究者提出了tsfresh（一种广泛使用的知名Python包）以加速这一过程。它不仅提供63种时间序列表征方法（可计算794个时间序列特征），还基于“基于可扩展假设检验的特征提取（FRESH）”算法[45]实现特征提取和选择的自动化——该算法在特征数量、设备/样本数量和不同时间序列数量方面具有线性可扩展性。然而，由于特征计算成本随其复杂度变化，调整计算的特征会显著改变tsfresh的运行时间。

5.3.3 22个典型时间序列特征（catch22）[154]

catch22是从高比较性时间序列分析（hctsa）[67]工具箱中提炼出的广泛使用的特征集——hctsa的完整版本包含超过7700个时间序列特征，过滤版本包含4791个特征。尽管hctsa能够为特定应用选择合适的特征，但计算成本高且存在冗余评估。受此启发，catch22的作者构建了一个数据驱动的流程，包括统计预过滤、性能过滤和冗余最小化。值得注意的是，在冗余最小化阶段，作者基于特征性能向量之间的皮尔逊相关系数（PC），采用带全链接的层次式聚类将过滤后的高性能特征分为22个簇，并基于特征的简洁性和可解释性手动选择特征。该流程最终得到22个典型特征，在平均仅损失7%分类准确率的情况下，大幅提升了计算效率和可扩展性。此外，catch22捕捉了时间序列数据中多样且具代表性的特征，其提炼的特征分为7类：分布特征、简单时间统计特征、线性和非线性自相关特征、连续差分特征、波动分析特征及其他特征。

表5 基于特征的聚类方法汇总

方法名称	聚类方式	特征类型	距离度量	维度（Dim）
TSC-GC-ED [235]	SOM	全局特征	欧氏距离（ED）	单变量（I）
CBC [234]	任意（*）	综合特征	任意（*）	单变量（I）
TSC-SSF [236]	任意（*）	统计特征	任意（*）	多变量（M）
TSC-SF-EU [196]	k-Means	统计特征	欧氏距离（ED）	多变量（M）
TSBF [21]	任意（*）	统计特征	欧氏距离（ED）	多变量（M）
hctsa [66]	线性	综合特征	任意（*）	单变量（I）
FBC [1]	FBC	模糊特征	欧氏距离（ED）	单变量（I）
TSA-CF [65]	任意（*）	综合特征	任意（*）	多变量（M）
tsfresh [44]	任意（*）	综合特征	任意（*）	多变量（M）
catch22 [154]	任意（*）	典型特征	任意（*）	多变量（M）
TSC-CN [30]	社区检测	可见性图特征	欧氏距离（ED）	多变量（M）
TSC-SFLP-ED [43]	k-Means	统计特征+负载曲线	欧氏距离（ED）	单变量（I）
FeatTS [224, 225]	k-Medoid	TSfresh特征	欧氏距离（ED）	单变量（I）
TSC-FDDO [265]	密度峰值搜索	综合特征	欧氏距离（ED）	单变量（I）
TSC-GPF-ED [91]	k-Means	全局特征+峰值特征	欧氏距离（ED）	单变量（I）
AngClust [132]	亲和传播	角度特征	皮尔逊相关（PC）	多变量（M）
FGHC-SOME [242]	SOM	统计特征	皮尔逊相关（PC）	多变量（M）
FTSCP [57]	任意（*）	综合特征	欧氏距离（ED）	多变量（M）
TSC-VF [240]	任意（*）	视觉特征	任意（*）	单变量（I）

注：I：单变量；M：多变量；*：任意。
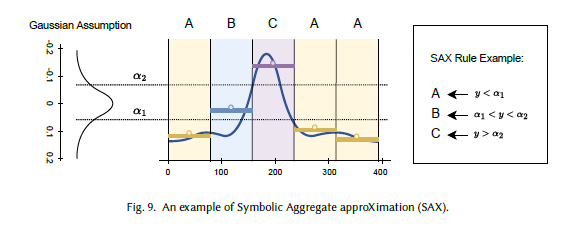
在这里插入图片描述

图9 符号聚合近似（SAX）示例

5.4 基于编码的方法

基于编码的时间序列聚类方法构建原始数据空间与变换空间（又称latent空间）之间的映射函数 $\to X'$ ，这一过程可视为编码过程。与使用原始数据的时间序列聚类方法相比，编码后的新表示 $X^{'}$ 捕捉了原始信号的关键信息，且维度可能大幅降低。凭借这一优势，新表示 $X^{'}$ 通常是下游过程的更优选择，具有更优的性能和更低的计算成本。所有基于编码的方法汇总于表6。

需注意的是，尽管基于特征的聚类和基于编码的聚类均为聚类生成新的数值序列，但两者的定义存在关键区别：基于特征的聚类方法依赖领域知识手动选择描述性特征（例如fMRI数据中的激活强度和延迟），而基于编码的聚类方法通过离散傅里叶变换、分段线性近似（PLA）等显式函数自动分解信号成分。

通常，映射函数 $F$ （基于编码的时间序列聚类方法的核心部分）可通过预定义的数学公式表示（如傅里叶变换）。下文将探讨代表性方法。

表6 基于编码的聚类方法汇总

方法名称	聚类方式	编码方式	距离度量	维度（Dim）
MKM [238]	改进k-Means	LPC系数	改进Itakura距离	单变量（I）
CA-CTS [211]	凝聚式层次聚类	PCA	欧氏距离（ED）	多变量（M）
CDM [116]	层次式聚类	SAX	CD	I-kMeans [146]
TSC-CR-LB [197]	k-Means	截断（Clipped）	LB_clipped	单变量（I）
SAX [145]	层次式/划分式	SAX	MINDIST	单变量（I）
TSC-ICA-SDA [82]	改进k-Means	ICA	未知（Unknown）	单变量（I）
ICTS-FC [2]	FCM	DWT	最长公共子序列（LCS）	单变量（I）
TSC-DSA-DTW [81]	k-Means	DSA	DTW	单变量（I）
TTC [5]	混合式	PAA	ED+DTW	单变量（I）
SAX Navigator [206]	凝聚式层次聚类	SAX	MINDIST变体	单变量（I）
SPIRAL [131]	保留DTW特性	SPIRAL	DTW	多变量（M）

注：I：单变量；M：多变量；/：无指定。

5.4.1 离散傅里叶变换（DFT）

离散傅里叶变换（DFT）是数字信号处理（DSP）中最常用的数学技术之一，也是时间序列领域的核心研究内容。通常，DFT将长度为 $N$ 的原始数据序列 $\{x_0, x_1, \cdots, x_{N-1}\}$ 转换为频域中的复数值序列 $\{X_0, X_1, \cdots, X_{N-1}\}$ ，公式如下（式15）。研究发现，频域中的新表示具有良好的可解释性：低频成分通常捕捉原始数据中随时间缓慢变化的信号，而高频成分则更关注快速变化的信号。在实际场景中，低频成分很可能揭示原始数据的主导趋势，而背景噪声通常由高频成分表示。

$X_k = \sum_{n=0}^{N-1} x_n \cdot e^{-\frac{i2\pi}{N}kn}$

5.4.2 主成分分析（PCA）

PCA[189]是一种经典且知名的降维技术，其核心目标是将高维数据集编码为低维表示，同时尽可能保留原始信息。在执行PCA之前，必须将每个变量的均值归一化为0——这一预处理步骤可消除主成分中的偏差。得到均值调整后的数据后，计算对称协方差矩阵 $A$ 以分析变量间的相关性。在此基础上，PCA需计算协方差矩阵 $A$ 的特征向量 $v$ 和特征值 $\lambda$ （式16），以确定主成分——主成分相互正交，且捕捉原始数据中变化最大的方向。值得注意的是，第一主成分对应数据变化最大的方向，第二主成分对应变化第二大的方向，以此类推。

由于协方差矩阵的特征向量定义与主成分一致，PCA会根据特征值的降序对特征向量进行排序，选择部分特征向量并以列的形式构成特征矩阵 $U$ ，然后将行方向为均值调整后原始数据的矩阵投影到所选主成分上，得到最终数据 $X^{'}$ ，公式如下（式16）：

$\lambda v, \ X' = X \cdot U \tag{16}$

5.4.3 分段聚合近似（PAA）

给定长度为 $n$ 的时间序列 $x = \{x_1, x_2, ..., x_n\}$ ，PAA[114]将其编码为长度为 $w$ 的向量 $p = \{p_1, p_2, ..., p_w\}$ （其中 $w$ 由用户指定且 $\ll n$ ）。PAA将时间序列划分为 $w$ 个等长的帧，计算每个帧的均值，由这些均值构成的向量即为PAA表示（式17）：

$p_i = \frac{w}{n} \sum_{j=\frac{n}{w}(i-1)+1}^{\frac{n}{w}i} x_j,$

其中 $p$ 中的每个元素 $p_i$ 可通过上述公式由 $x$ 中的元素 $x_j$ 计算得出。

5.4.4 符号聚合近似（SAX）

SAX[144]是另一种值得关注的符号化时间序列表示方法，图9展示了SAX的示例。给定长度为 $n$ 的时间序列，SAX将其简化为长度为 $w$ 的字符串（ $w$ 由用户定义且 $\ll n$ ）。首先对时间序列进行Z标准化，然后应用PAA表示：将时间序列划分为 $w$ 个等长帧，计算每个帧的均值并拼接为向量 $P = \{p_1, p_2, ..., p_w\}$ 。

由于标准化后的时间序列近似服从高斯分布，给定字母表大小 $\alpha$ ，SAX会确定断点 $\{b_1, b_2, ..., b_{\alpha-1}\}$ （其中 $b_0$ 和 $b_{\alpha}$ 分别定义为 $-\infty$ 和 $+\infty$ ）——这些断点将标准高斯曲线 $N (0, 1)$ 划分为 $\alpha$ 个等面积区域，每个区域的面积均为 $\frac{1}{\alpha}$ 。基于得到的PAA表示和断点，SAX将所有PAA系数与断点进行比较，确定每个PAA系数所属的区间，并分配与该区间关联的字母以表示对应PAA帧。最终表示为 $S = \{s_1, s_2, ..., s_w\}$ ，其中每个 $s_i$ 由以下函数计算：

$s_i = alpha_j, \ \text{若} \ b_{j-1} \leq p_i < b_j \quad (18)$

式中 $alpha_j$ 表示与区间 $b_{j-1}, b_j)$ 关联的字母。

6 基于子序列的方法

如2.2节所述，基于子序列的聚类是全时间序列聚类中的一种特殊情况。与划分式、编码式等传统聚类方法不同，基于子序列的方法通过一个或多个子序列表示完整时间序列——例如，具有相似形状子（shapelet）的时间序列可被归为同一簇。需特别注意的是，与2.2节中的“子序列聚类”不同，基于子序列的聚类方法最终仍为完整时间序列分配单个标签，这与本文定义的“全时间序列聚类”完全一致。基于子序列的方法可进一步分为两类：基于滑动窗口的方法（6.1节）和基于形状子的方法（6.2节），相关方法汇总于表7。

表7 基于子序列的聚类方法汇总

方法名称	二级分类	距离度量	维度（Dim）
U-Shapelets [257]	形状子（Shapelets）	LN-ED	单变量（I）
SUSh [229]	形状子（Shapelets）	ED	单变量（I）
USLM [261]	形状子（Shapelets）	软最小函数（Soft minimum function）	单变量（I）
LDPS [152]	形状子（Shapelets）	卷积得分（Convolutional score）	单变量（I）
USSL [262]	形状子（Shapelets）	ED	单变量（I）
FOTS [62]	形状子（Shapelets）	FOTS	单变量（I）
LSH-us [156]	形状子（Shapelets）	LN-ED	单变量（I）
Trendlets [107]	形状子（Shapelets）	沃德距离（Ward Distance）	单变量（I）
ShapeNet [135]	形状子（Shapelets）	ED	多变量（M）
SPF [139]	形状子（Shapelets）	布尔值（Boolean）	多变量（M）
MUSLA [260]	形状子（Shapelets）	ED	多变量（M）
TSC-BLU [108]	形状子（Shapelets）	LN-ED	多变量（M）
CDPS [55]	形状子（Shapelets）	DTW+ED	单变量（I）
CSL [141]	形状子（Shapelets）	多距离（Multiple Distance）	多变量（M）
MSCPF [200]	滑动窗口（Sliding Window）	ED	多变量（M）
TS3C [80]	滑动窗口（Sliding Window）	ED	单变量（I）
TCMS [137]	滑动窗口（Sliding Window）	ED	单变量（I）
MPNCMI [136]	滑动窗口（Sliding Window）	ED	单变量（I）

注：I：单变量；M：多变量。

6.1 基于滑动窗口的方法

与之前考虑所有时间步比较时间序列的方法不同，基于滑动窗口的方法通过更小的范围（即滑动窗口）解决聚类问题。如2.1节所述，滑动窗口是通过滑动固定长度的“窗口”提取的一组子序列，这些子序列可用于提供特征信息，或直接作为时间序列相似性度量的一种方式。该类别主要包含两个研究方向：（1）矩阵轮廓（Matrix Profile）；（2）子序列聚类，相关方法汇总于表7。

6.1.1 矩阵轮廓

矩阵轮廓[254, 267]是一种可扩展的子序列级时间序列全对相似性搜索算法。通过滑动窗口机制，该算法能高效提取潜在子序列并进行匹配，对模式发现（motif discovery）和异常检测（discord detection）均有帮助。矩阵轮廓包含两个核心组件：矩阵轮廓向量和矩阵轮廓索引，定义如下：

定义6.1（矩阵轮廓[254]）：时间序列 $A$ 和 $B$ 的矩阵轮廓 $P_{AB}$ 是相似连接集 $J_{AB}$ 中每对元素的标准化欧氏距离向量——其中 $J_{AB}$ 是通过滑动窗口提取的所有子序列对 ${(A_i, B_j)\}$ 的集合，且集合中的每对元素均为最近邻。

定义6.2（矩阵轮廓索引[254]）：时间序列 $A$ 和 $B$ 的矩阵轮廓索引 $I_{AB}$ 是一个索引向量，若 ${(A_i, B_j)\}$ 是相似连接集中的最近邻对，则 $I_{AB}[i] = j$ 。

由定义可知，矩阵轮廓 $P_{AB}$ 和轮廓索引 $I_{AB}$ 可视为两条时间序列间的元数据或特殊格式的距离度量。TCMS[137]将两条时间序列的相关度定义为匹配子序列的数量（即通过矩阵轮廓找到的最相似子序列数量），并将时间序列数据集转换为图网络——其中每个节点代表一条时间序列，边代表相关度。为解决聚类问题，采用社区检测算法对该网络进行划分。

MPNCMI[136]在相似性度量过程中采用矩阵轮廓寻找相似子序列，将正态云模型应用于子序列对以过滤成对信息，然后在复杂网络上执行社区发现以获取聚类结果。

6.1.2 子序列聚类

以往研究还探索了通过多阶段方式进行时间序列聚类的可能性：基于滑动窗口提取子序列后，先执行子序列聚类以获取初步特征信息，再在最终阶段进行全时间序列聚类。

MSCPF[200]提出了一种基于动态滑动时间窗口（DSTW）的多阶段滑动窗口聚类算法：第一阶段对分段信息执行子序列聚类，第二阶段对小型分段簇进行聚合，得到最终聚类结果。这种多阶段聚类还为后续时间序列预测任务奠定了基础。TS3C[80]采用类似思路，但未在滑动窗口后执行传统子序列聚类，而是采用最小二乘多项式分段策略，将每条时间序列通过所有分段的特征信息映射为新表示，用于后续聚类。

6.2 基于形状子的方法

基于形状子的方法是子序列级时间序列聚类的另一类重要方法。研究发现，时间序列中一些重复出现的子序列可作为表征时间序列的有意义模式，这类子序列被称为形状子[253]。随着数据挖掘技术的发展，越来越多基于形状子的方法被提出，用于时间序列聚类任务中的鲁棒形状子搜索[62, 152, 229, 257, 261, 262]。本节遵循[253, 257]中对形状子的定义，相关方法汇总于表7。图10展示了通用形状子变换流程：通过一组学习到的形状子，将每条时间序列投影到新的表示空间（投影方式为计算完整序列与形状子的距离）；同一组的时间序列在该新空间中会更接近，为聚类过程提供关键指导。

定义6.3（形状子）：给定包含多个类别的时间序列数据集，形状子是对时间序列类别具有强预测性的子序列时间序列。
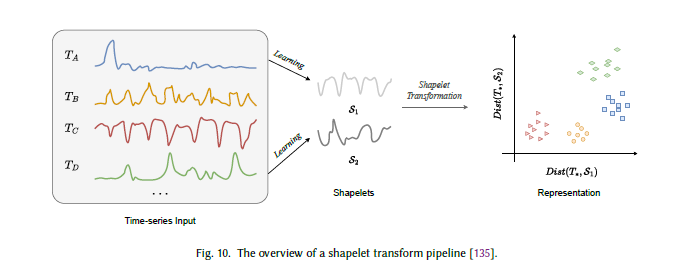
在这里插入图片描述

图10 形状子变换流程概述[135]

6.2.1 U-Shapelets与SUSh

U-Shapelets[257]提出了一种从无标签时间序列数据集中搜索形状子的新方法——通过不同子序列最大化簇间分离差距。计算形状子与给定时间序列的子序列距离 $s d i s t$ ，可轻松得到距离矩阵；该距离矩阵可进一步应用于k-Means等多种聚类算法。然而，U-Shapelets的整体时间复杂度较高，难以应用于大规模数据集。为解决这一问题，研究者提出了可扩展U-Shapelets（SUSh）[229]，在保证性能无显著损失的前提下实现形状子的可扩展发现。SUSh采用带随机掩码的SAX表示加速时间序列间的相似性度量——其中比较过程中的冲突次数可作为形状子质量的重要指标。实验表明，SUSh的时间复杂度可降低两个数量级。

6.2.2 USLM与LDPS

无监督形状子学习模型（USLM）[261]则采用了与上述不同的思路：不再通过耗时的搜索过程，而是为无标签时间序列数据设计高效的形状子学习策略。在该过程中，候选形状子 $\dot{s}$ 、分类边界 $W$ 和伪类标签 $Y$ 通过带形状子变换的最小二乘优化问题进行联合优化。

学习DTW保留形状子（LDPS）[152]提出了一种无标签场景下DTW保留形状子的新学习策略，其核心目标是通过欧氏空间中的形状子变换近似原始空间中的DTW距离。值得注意的是，形状子变换与形状子匹配的形式与卷积神经网络（CNN）具有天然相似性，这为LDPS的卷积变体应用奠定了基础。

6.2.3 深度学习驱动的形状子方法

随着深度神经网络的发展，越来越多的研究聚焦于深度学习策略在形状子学习中的应用。CSL[141]提出了一种多粒度对比策略，用于多变量时间序列数据的形状子学习：在该框架中，形状子表示为可学习参数，采用形状子变换器作为编码器获取潜在嵌入；考虑到序列长度变化的问题，设计多尺度对齐机制以保持各层级的一致性。作为一种无监督表示学习算法，CSL可生成适用于多种时间序列下游任务的形状子基表示。

7 基于表示学习的方法

近几十年来，深度学习的兴起催生了大量时间序列聚类方法，这些方法充分利用深度神经网络强大的表示能力。本节首先概述基于表示学习的方法的核心组件（7.1节），然后综述代表性算法——分为基于比较的方法（7.2节）和基于生成的方法（7.3节）。表8汇总了所有被综述的方法。

7.1 时间序列表示学习概述

表示学习已在计算机视觉、自然语言处理等多个研究领域得到广泛应用。早期研究发现，尽管深度神经网络对人类而言多为“黑箱”，但其某些层的输出特征图能够提取有意义的特征信息（如边缘或重复模式）。在许多情况下，通过精心设计的模型架构在大规模数据集上预训练得到的表示具有高度鲁棒性，且易于适配下游任务。由于学习到的表示维度远低于原始数据，这类技术在输入长度可能极高的时间序列领域被广泛用作降维策略。图11展示了学习到的表示（通过T-SNE可视化）示例。
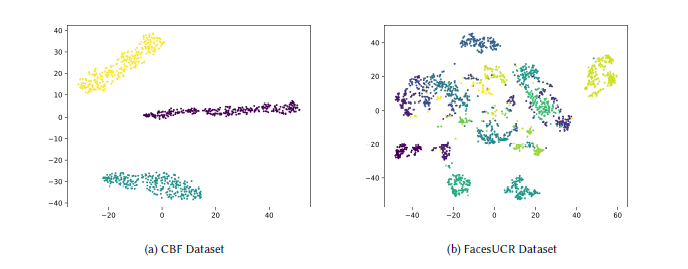
在这里插入图片描述

图11 UCR数据集上表示学习策略得到的编码表示的T-SNE可视化。左：含3个簇的CBF数据集；右：含14个簇的FacesUCR数据集。

通常，根据学习策略的设计，表示学习可分为三类：监督学习、半监督学习和无监督学习。在本文的时间序列聚类任务背景下，我们主要关注无监督学习（也包含部分半监督技术）。基于表示学习的聚类方法的整体流程可总结如下：

预训练阶段：给定设计好的模型和训练集，预训练阶段的目标是学习适用于时间序列聚类的代表性潜在空间。
聚类阶段：将预训练模型得到的表示作为输入，应用k-Means、k-Shape等传统聚类方法进行聚类。

根据[130]的研究，基于时间序列表示学习的聚类方法包含三个核心组件：（1）模型架构；（2） pretext损失（预训练损失）；（3）聚类损失。模型架构影响整体性能和推理速度，而pretext损失与聚类损失的设计决定潜在空间的结构。下文将详细探讨每个组件。

7.1.1 模型架构

深度学习模型（包括时间序列聚类领域的模型）存在多种架构设计，其中最基础的包括全连接神经网络（FCN）、卷积神经网络（CNN）、循环神经网络（RNN）、注意力机制神经网络和图神经网络（GNN）。

全连接神经网络（FCN）

全连接神经网络（FCN）又称多层感知机（MLP），是深度学习模型中最基础的架构之一，源于神经科学中的概念[203]。它提出了一种名为“感知机”的假设神经系统：每个感知机通过可学习权重和激活函数实现多输入到单输出的映射（图12）。为提取不同特征，可将多个感知机跨层堆叠，生成维度通常低于原始输入的输出。基于这一思路，不同的FCN基模型已在多个领域被提出[83, 244]。
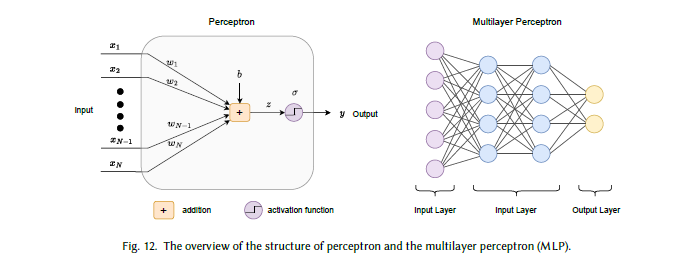
在这里插入图片描述

图12 感知机与多层感知机（MLP）结构概述

卷积神经网络（CNN）

CNN已被广泛用作基础架构，尤其在计算机视觉任务中。VGG[214]、AlexNet[127]、ResNet[85]等代表性CNN模型在图像分类、检测、分割等任务中取得了巨大成功。如图13所示，每个卷积层包含 $m$ 个大小为 $k$ 的核（kernel）——这些核可视为过滤器，以滑动窗口的方式扫描输入数据，在多个维度上搜索特定模式。与FCN设计相比，CNN层的核设计可在所有维度（或通道）上重复应用，因此所需参数远少于全连接层。最常用的卷积层格式为二维（用于图像）或一维（用于语音、文本和时间序列数据）。
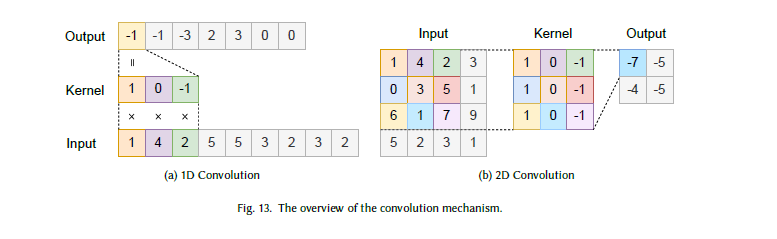
在这里插入图片描述

图13 卷积机制概述。（a）一维卷积；（b）二维卷积

循环神经网络（RNN）

然而，全连接神经网络和卷积神经网络存在一个共同问题：无法处理变长输入——而变长输入是语音、文本、通用时间序列等数据格式的核心特征。为解决这一问题，研究者提出了循环神经网络（RNN）[42, 88, 90]，它已成为语音识别、机器翻译、时间序列聚类等多个研究领域的重要模型架构。与传统前馈神经网络不同，RNN的内部记忆机制使其能够逐步接收输入，并递归更新隐藏状态（图14）。长短期记忆网络（LSTM）[88]和门控循环单元（GRU）[42]是代表性RNN模型，已在多个领域取得成功。

传统RNN中隐藏状态 $h_t$ 的更新规则（时间步 $t$ ）可表示为（式20）：

$h_t = \tanh(W_h h_{t-1} + W_x x_t + b), \tag{20}$

其中 $x_t$ 和 $h_t$ 分别表示时间步 $t$ 的输入和隐藏状态， $W_h$ 、 $W_x$ 和 $b$ 表示RNN设计中的可学习权重。需注意的是，与FCN、CNN类似，RNN也可构建多层结构。
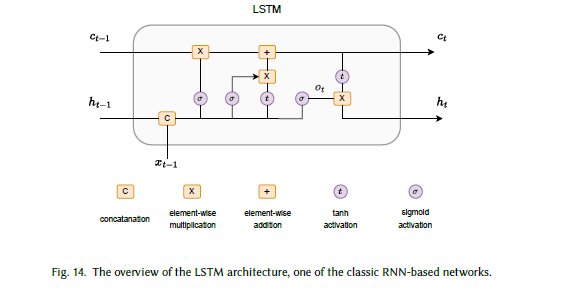
在这里插入图片描述

图14 经典RNN基网络——LSTM架构概述

注意力机制神经网络

注意力机制是一种广泛认可的深度学习架构，最早在文献[16]中提出——它引入了编码器与解码器之间的软对齐机制，显著提升了神经机器翻译的性能。2017年，Vaswani等人在“Attention is all you need”一文中提出了Transformer架构[231]，该架构迅速成为自然语言处理（NLP）、计算机视觉（CV）等多个研究领域的主导模型架构。注意力机制描述了从查询（query）、键（key）、值（value）三元组到输出的映射函数——其中每个组件均可由每层的输入建模得到。注意力机制具有良好的可解释性和优异的性能，同时通过并行计算大幅降低了计算时间。Transformer是最重要的注意力基架构之一（图15），给定查询 $Q$ 、键 $K$ 和值 $V$ ，注意力机制可表示为（式21）：

$\text{softmax}\left(\frac{Q K^T}{\sqrt{d_k}}\right) V, \tag{21}$

其中 $\frac{1}{\sqrt{d_k}}$ 是基于键的维度 $d_k$ 的缩放因子。
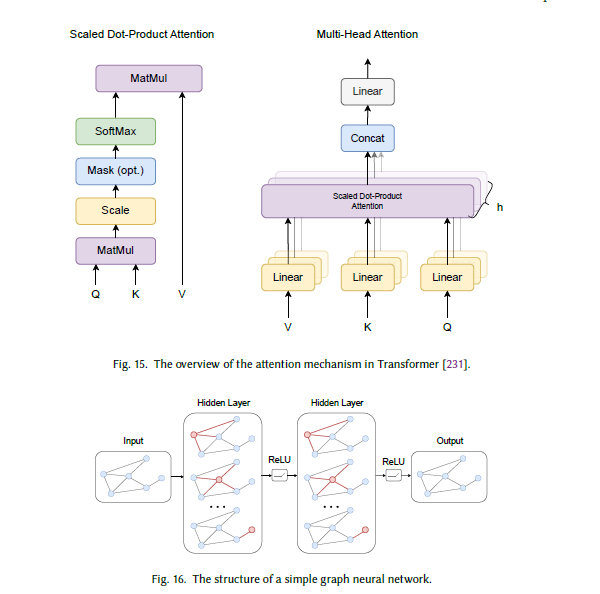
在这里插入图片描述

图15 Transformer中注意力机制概述[231]

图神经网络（GNN）

图是最重要的数据结构之一，已在多个研究领域得到广泛探索——它由节点/顶点和边组成。随着深度神经网络的发展，图神经网络（GNN）受到广泛关注，尤其在数据样本间关系对问题求解至关重要的场景中。GNN存在多种架构，如图卷积网络（GCN）[121]、图采样与聚合网络（GraphSAGE）[84]、图注意力网络（GAT）[232]等。

在时间序列分析中，每个数据样本可视为高维空间中的一个节点，节点间的边可定义为相似性或距离值。考虑到GNN在学习结构信息方面的优势，以往研究将GNN模块与传统深度神经网络（DNN）模块结合，为时间序列聚类获取更优表示[29]。GNN层中消息传递与聚合的通用形式可表示为（式22）：

$h_v^{(k)} = f^{(k)}\left( W^{(k)} \cdot \frac{\sum_{u \in \mathcal{N}(v)} h_u^{(k-1)}}{|\mathcal{N}(v)|} + B^{(k)} \cdot h_v^{(k-1)} \right) , \tag{22}$

其中 $h_v^{(k)}$ 表示节点 $\in V$ 经过第 $k$ 层后的嵌入， $\mathcal{N}(v)$ 表示节点 $v$ 的邻域， $W^{(k)}$ 和 $B^{(k)}$ 是可学习权重， $f^{(k)}$ 表示第 $k$ 层的激活函数。图16展示了简单图神经网络的结构。
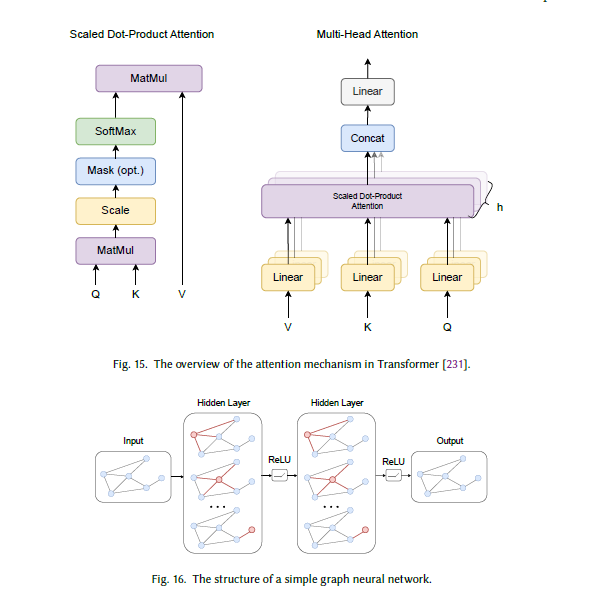
在这里插入图片描述

图16 简单图神经网络结构

7.1.2 Pretext损失（预训练损失）

根据[130]的研究，第一阶段表示学习的目标函数可分为两类：pretext损失是其中之一，用于帮助模型学习有意义的特征。但需注意，pretext损失的设计通常针对通用时间序列分析，而非专门针对聚类任务。为解决这一问题，许多方法在预训练阶段融入聚类损失，为潜在空间提供特定约束流形。本节将重点探讨pretext损失。

重构损失（REC）

重构损失是通用表示学习中最常用的损失函数之一。通过最小化原始输入与重构输出之间的误差，自编码器（AE）能够学习到可用于数据表示的有意义特征，且这些特征的维度通常远低于原始数据。重构损失的公式如下：

$\mathcal{L}_{REC} = \frac{1}{N} \sum_{i=1}^N \left\| X_i - \mathcal{D}(\mathcal{E}(X_i)) \right\|^2,$

其中 $X_i$ 是数据集中的第 $i$ 个输入（数据集共含 $N$ 个样本）， $\mathcal{E}$ 和 $\mathcal{D}$ 分别表示自编码器的编码器和解码器模块。通常，重构损失采用上述公式中的L2范数。

多阶段重构损失（MREC）

MREC是重构损失的扩展版本，在每个层级计算损失——这种分层设计为表示学习施加了更强的约束。需注意的是，编码器与解码器的模型设计需满足对称结构。MREC的公式如下（式24）：

$\mathcal{L}_{MREC} = \frac{1}{N} \sum_{i=1}^N \sum_{j=1}^L \left\| o_{\mathcal{D}_j}^i - o_{\mathcal{E}_j}^i \right\|^2, \tag{24}$

其中 $o_{\mathcal{E}_j}^i$ 和 $o_{\mathcal{D}_j}^i$ 分别表示编码器第 $j$ 层和解码器第 $j$ 层的输出。

变分自编码器损失（VAE）

变分自编码器（VAE）是自编码器（AE）最著名的变体之一，旨在提升模型对新数据的泛化能力。VAE引入KL散度约束，将学习到的潜在空间的概率分布与预定义先验分布（通常为高斯分布）进行正则化。VAE损失的公式如下：

$\mathcal{L}_{VAE} = \sum_{i=1}^N -\mathbb{E}_{z_i \sim q(z_i | x_i)} \left[ \log p(x_i | z_i) \right] + KL\left( q(z_i | x_i) \| p(z_i) \right),$

其中 $z_i$ 是输入数据 $x_i$ 的学习到的潜在表示， $p(z_i)$ 是预定义先验分布， $q(z_i | x_i)$ 和 $p(x_i | z_i)$ 是两个可通过深度神经网络建模的条件分布。

三元组损失（TRPLT）

三元组损失是对比学习中广泛使用的重要目标函数设计之一。给定锚点数据样本，通过精心选择相似/不相似数据样本定义正样本对和负样本对，其核心目标是缩小相似数据样本的学习表示之间的距离，扩大不相似样本表示之间的距离。三元组损失的公式如下：

$\mathcal{L}_{TRPLT} = -\log \left( \sigma\left( \mathcal{E}(X)^{\top} \mathcal{E}(X^+) \right) \right) - \sum_{k=1}^K \log \left( \sigma\left( -\mathcal{E}(X)^{\top} \mathcal{E}(X_k^-) \right) \right),$

其中 $X$ 是锚点样本， $X^+$ 和 $X^-$ 分别表示正样本和负样本， $\sigma$ 表示sigmoid函数， $K$ 表示负样本对的数量。

InfoNCE损失

InfoNCE损失是对比学习中另一种广泛使用的损失设计，在SimCLR[39]等无监督表示学习工作中得到应用。与三元组损失类似，InfoNCE损失同样强制模型捕捉数据对（如正样本对、负样本对）之间的距离关系。以下以SimCLR[39]中的公式为例进行说明（式27）：

$\mathcal{L}_{InfoNCE}(i, j) = -\log \frac{exp \left( sim(z_i, z_j) / \tau \right)}{\sum_{k=1}^{2N} \mathbb{1}_{[k \neq i]} exp \left( sim(z_i, z_k) / \tau \right)} \tag{27}$

其中 $z_i$ 和 $z_j$ 是数据集中第 $i$ 个和第 $j$ 个数据样本的学习表示， $sim(\cdot)$ 是向量间的相似性函数， $\mathbb{1}$ 表示指示函数， $N$ 是训练过程中的批大小（batch size）， $\tau$ 是温度参数。

7.1.3 聚类损失

如前所述，pretext损失可用于通用深度表示学习，但可能无法专门解决聚类任务中的问题。本节列出文献中7种广泛使用的聚类损失，以应对这一挑战。

DEC损失

该损失最早在DEC[244]中提出，用于无监督深度嵌入学习。DEC引入辅助目标分布，帮助学习适用于聚类分析的表示，损失以KL散度形式定义（式28）：

$\mathcal{L}_{DEC} = KL(P \| Q), \tag{28}$

其中 $P$ 表示辅助目标分布， $Q$ 表示软聚类分配分布， $N$ 和 $K$ 分别表示批大小和簇数量。

IDEC损失

IDEC[83]是DEC[244]的扩展版本，它将欠完备自编码器与聚类损失（DEC损失）结合，以更好地保留局部结构。 $\gamma$ 是平衡两项损失的超参数：当 $\gamma=0$ 时，IDEC损失与DEC损失完全一致。IDEC损失的公式如下（式29）：

$\mathcal{L}_{IDEC} = (1-\gamma) \mathcal{L}_{DEC} + \gamma \mathcal{L}_{REC}, \quad (29)$

DEPICT损失

与IDEC损失类似，DEPICT[71]也将聚类导向损失与重构损失结合；但与IDEC损失不同，DEPICT的目标分布 $P$ 也参与优化过程。DEPICT损失的公式如下（式30）：

$\mathcal{L}_{DEPICT} = KL(P \| Q) + KL(f \| u) + \mathcal{L}_{MREC}, \quad (30)$

其中 $f$ 和 $u$ 分别表示经验标签分布和均匀先验分布。在该研究中，目标分布 $P$ 通过“清洁路径（clean pathway）”设计计算得到。

SDCN损失

SDCN[29]利用图神经网络捕捉数据的结构信息，其整体目标函数包含重构损失、聚类损失和GCN损失（式31）：

$\mathcal{L}_{SDCN} = \mathcal{L}_{REC} + \alpha \mathcal{L}_{CLU} + \beta \mathcal{L}_{GCN}, \quad (31)$

其中 $\mathcal{L}_{CLU} = KL(P \| Q)$ ， $\mathcal{L}_{GCN} = KL(P \| Z)$ —— $Q$ 和 $Z$ 分别表示深度神经网络（DNN）和GCN模块的软聚类分配分布， $\alpha$ 和 $\beta$ 是平衡系数。

VaDE损失

VaDE[106]将VAE与高斯混合模型（GMM）结合，学习适用于聚类任务的深度表示，同时具备生成有意义样本的能力。VaDE损失的公式如下（式32）：

$\mathcal{L}_{VaDE} = \mathbb{E}_{q(z, c | x)} [\log p(x | z)] - D_{KL}(q(z, c | x) \| p(z, c)), \quad (32)$

其中 $\sim Cat(\pi)$ 表示簇， $p (z, c)$ 表示混合高斯（MoG）先验，整体目标函数以证据下界（ELBO）形式表示。

DTCR损失

DTCR[160]引入辅助分类模块以区分真实样本与伪造样本，同时引入k-Means目标函数学习簇特定表示。DTCR损失的公式如下（式33）：

$\mathcal{L}_{DTCR} = \mathcal{L}_{REC} + \mathcal{L}_{ADV} + \gamma \mathcal{L}_{K-Means}, \quad (33)$

其中 $\mathcal{L}_{ADV}$ 类似于生成对抗网络（GAN）中的判别器损失，在训练过程中采用交叉熵损失形式， $\gamma$ 是平衡系数。

ClusterGAN损失

ClusterGAN[70]提出一种基于GAN的模型，用于无监督学习有意义的表示。该模型引入聚类器模块 $c$ ，帮助学习从数据样本到潜在空间的映射。ClusterGAN损失的公式如下：

$\mathcal{L}_{ClusterGAN} = \min_{\mathcal{G}, C} \max_{\mathcal{D}} \mathbb{E}_{X \sim p(X)} \left[ \log \mathcal{D}(C(X), X) \right] + \mathbb{E}_{Z \sim p(Z)} [\log (1 - \mathcal{D}(Z, \mathcal{G}(Z)))] ,$

其中 $\mathcal{G}$ 是生成器， $\mathcal{D}$ 是判别器， $C$ 是聚类器， $X$ 是真实数据， $Z$ 是噪声输入。

7.2 基于比较的方法

与基于编码的方法等传统聚类方法类似，基于比较的时间序列聚类方法也通过映射函数 $\varepsilon: X \to Z$ 将时间序列表示为潜在向量（通常维度大幅降低），以用于下游任务。但不同的是，在这类方法中，编码映射函数通过神经网络以比较方式（如对比学习（CNRV）或生成对抗网络（ADV））学习得到。所有相关方法汇总于表8。

7.2.1 对比学习（CNRV）

对比学习（CNRV）是当前无监督深度学习中应用最广泛的技术之一，已在计算机视觉、自然语言处理、语音识别等多个研究领域取得巨大成功。给定一个锚点数据样本，寻找相似和不相似的样本以构建正样本对和负样本对；对比学习的目标是学习鲁棒表示，使正样本对之间的距离缩小，负样本对之间的距离扩大（图17）。这种策略与划分式方法等聚类技术的核心思想天然契合，因此近年来受到广泛关注。本节将先介绍对比学习中常用的损失函数，再综述相关方法。
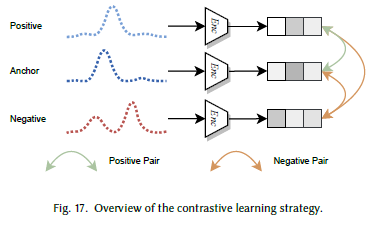
在这里插入图片描述

图17 对比学习策略概述

对比学习在通用机器学习中存在多种目标函数设计，其中两种主要损失函数在时间序列对比学习中应用广泛：三元组损失[63, 169]和InfoNCE损失[39, 172]（见式26和式27）。两者均在无监督表示学习中取得了显著成功，并在多个下游任务中表现出优异性能。

根据负样本数量 $K$ 的不同，实验中可设置一个或多个负样本对； $\tau$ 是控制分布的温度参数[241]。通过精心选择正样本和负样本，模型能够以对比方式学习有意义的表示。从对比视角出发，可将对比策略分为三类：时间对比（Temporal Contrast）、实例对比（Instance-wise Contrast）和多视图对比（Multi-view Contrast）。需注意的是，时间对比和实例对比的概念也与本文定义的两类全时间序列聚类（子序列级聚类或完整时间序列级聚类）高度契合。

时间对比（Temporal Contrast）

时间对比最早在文献[63]中提出，用于解决无监督学习场景下正/负样本对选择的挑战。在有标注的情况下，可轻松确定给定锚点时间序列样本对应的正/负样本；但在无监督表示学习中，这类指导信息不可得。受word2vec思想的启发，一种解决方案是利用上下文自动生成正/负样本对：给定时间序列样本 $x$ 中的随机子序列 $x^{ref}$ ，假设 $x^{ref}$ 内部的任何子序列 $x^{pos}$ 都应具有相似表示；相反，从其他随机时间序列中提取的任何子序列 $x^{neg}$ 都应被视为与 $x^{ref}$ 距离较大的负样本。该方法采用三元组损失（T-Loss）作为目标函数，大量实验表明，学习到的表示在时间序列聚类任务中表现优异。

时间邻域编码（TNC）[226]采用与上述类似的概念，但未使用T-Loss，而是通过判别器近似“一个子序列是另一个子序列的邻域”的概率（基于编码器的潜在表示）。然而，上述方法均未解决正/负样本对的选择问题。以往研究发现，局部方差最小的锚点可能导致性能下降[38]，因此研究者提出“对比三元组选择（Contrastive Triplet Selection）”策略——基于欧氏距离计算的局部方差和相似性关系，选择有意义的子序列样本 $x^{ref}$ 、 $x^{pos}$ 、 $x^{neg}$ ，为模型学习提供更多指导。

实例对比（Instance-wise Contrast）

与子序列级的时间信息不同，实例对比试图从实例级（即完整时间序列）学习相似性关系。给定正样本对 ${x^{ref}, x^{pos}\}$ 和负样本对 ${x^{ref}, x^{neg}\}$ ，模型通过对比学习获取有意义的表示。需注意的是，此处所有输入（ $x^{ref}$ 、 $x^{pos}$ 、 $x^{neg}$ ）均为数据集中不同的完整时间序列，而非子序列。为生成可靠的三元组集合，研究者探索了多种策略：Ts2DEC[98]提出半监督深度嵌入聚类框架，利用真值标签生成三元组约束；而CCL[210]等方法则采用从学习表示中得到的弱簇标签。

在无监督场景下，三元组集合的生成面临与时间对比相同的问题。作为早期对比学习研究之一，SimCLR[39]探索了一种简单框架——通过数据增强生成图像对：同一数据样本的两个增强视图被视为正样本对，同一批中的不同样本互为负样本对。该策略在图像、时间序列等多种数据模态中均取得了成功。LDVR[9]采用相同概念，为时间序列数据提出无监督三元组选择策略：将时间序列转换为二维图像，以利用计算机视觉领域预训练模型（如ResNet[85]）的知识。DCRLS[243]将SimCLR的思想扩展到时间序列领域，通过多层相似性对比实现优异性能，并在框架中采用自蒸馏作为正则化手段进行知识传递。

与时间对比类似，部分研究也聚焦于三元组选择的不同采样策略。SleepPriorCL[259]提出基于知识的正样本挖掘策略，以解决对比学习中的采样偏差问题：利用预计算的相异度，在 mini-batch 内重新定义正样本对。实验表明，该方法在睡眠分期任务中相较于基准方法实现了性能提升。

多视图对比（Multi-view Contrast）

除上述两种对比类型外，近年来的研究还探索了结合多种视图进行鲁棒表示学习的可能性。TS2Vec[256]提出统一框架，以分层方式同时利用实例对比和时间对比；TS-TCC[56]引入跨视图任务，实现时间和上下文的双重对比。除时域外，研究者还探索了频域的可能性：TF-C[264]引入新的频率编码器，确保实例级样本对在时域和频域的一致性；同年，BTSF[251]也采用了频率一致性概念，通过迭代的“融合-压缩（fusion-and-squeeze）”方式优化双线性特征，以更好地捕捉时域和频域信息。

然而，上述策略主要关注通过对比学习进行通用表示学习，可能无法专门解决聚类任务中的问题。为此，研究者提出基于簇或原型的对比损失，以提升聚类质量[122, 138, 168]。与时间对比或实例对比类似，这类方法强制不同簇的表示具有可区分性。由于簇级对比学习难以单独优化，在这些研究中，它通常作为辅助损失用于多视图学习。

7.2.2 生成对抗网络（GAN）

生成对抗网络（GAN）[77]最初为高质量图像生成提出，包含两个核心组件：（1）生成器 $G$ ：用于捕捉真实数据分布；（2）判别器 $D$ ：用于估计给定样本是合成数据还是真实数据的概率。通过极小极大二人博弈（minimax two-player game）的新颖设计，生成器 $G$ 能够生成接近真实的合成数据，并在图像、视频、文本、时间序列等多种数据格式中取得了巨大成功。图18展示了经典GAN的结构。
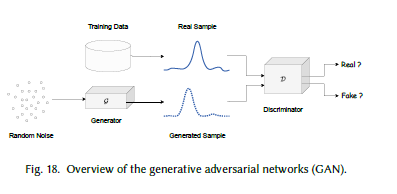
在这里插入图片描述

图18 生成对抗网络（GAN）概述

具体而言，给定噪声输入 $\sim p_z(z)$ ，生成器生成与真实数据 $\sim p_{data}$ 形状相同的伪造数据样本 $G (z)$ ；判别器的职责是预测给定数据 $x^{'}$ 为真实数据的概率（输出标量），伪造数据的概率则为 $1 - D (x^{'})$ 。最终，判别器 $D$ 试图对给定数据进行正确的二分类，而生成器 $G$ 则试图生成高质量数据以“欺骗”判别器。

定义价值函数 $V (D, G)$ ，GAN的整体目标以二人极小极大博弈形式定义（式34）：当判别器无法区分合成数据与真实数据，且生成器无法进一步优化时（即 $\frac{1}{2}$ ），损失最终收敛。

为从基于GAN的模型中提取知识，以往研究探索了多种技术：ClusterGAN[70]提出用于聚类任务的深度生成对抗网络，通过引入聚类器模块将真实数据映射为判别性表示；针对时间序列领域的问题，TCGAN[92]被提出——除生成器和判别器的常规设计外，TCGAN利用无监督学习过程中预训练的判别器构建表示编码器，以适配时间序列分类、聚类等下游任务。部分研究还聚焦于时间序列聚类的特定场景：例如，针对不完整时间序列聚类，CRLI[159]提出端到端方法，通过基于GAN的网络设计同时优化补全和聚类过程——在该场景中，生成器可视为输出鲁棒表示的编码器，用于后续聚类。

7.3 基于生成的方法

与基于比较的聚类方法不同，基于生成的时间序列聚类方法利用生成模型架构，通过对生成输出施加约束来学习鲁棒表示。该领域主要包含两种技术：（1）重构任务：给定输入数据，寻找能够重构原始数据的判别性潜在表示（包含关键特征信息）；（2）预测任务：给定时间步0到 $t - 1$ 的子序列，预测下一个时间步 $t$ 的值——为实现这一目标，也需通过编码过程进行特征提取和未来预测。通过上述两种技术，可找到维度可能更低的优良数据表示潜在空间，只需在该空间上应用简单的k-Means等方法即可得到最终聚类结果。相关方法汇总于表8。

7.3.1 基于重构的学习

自编码器（AE）是最早提出的用于降维、预训练、生成等多种任务的经典方法之一，其核心思想是重构[17, 22, 124, 205]。包括变分自编码器（VAE）[120]在内的多种变体，已在计算机视觉、机器翻译、语音识别等领域取得巨大成功。具体而言，自编码器包含两个核心部分：编码器 $\varepsilon: X \to Z$ （将输入 $x$ 映射到潜在空间 $z$ ）和解码器 $\to \hat{X}$ （从潜在空间 $z$ 生成重构数据 $\hat{X}$ ）（图19），其目标函数定义如式23所示。
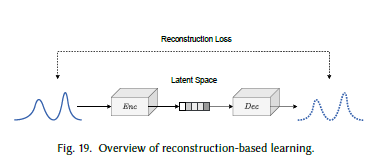
在这里插入图片描述

图19 基于重构的学习概述

鉴于自编码器的优异性能，研究者对基于AE的时间序列聚类技术进行了广泛探索：针对传统DEC[244]方法在嵌入空间中可能存在的失真问题，IDEC[83, 162]提出在聚类损失中加入重构约束，以更好地捕捉数据的结构信息；DEPICT[71]扩展了这一思想，在去噪自编码器的每个层级应用重构损失，并将噪声编码器、解码器、清洁编码器等多个组件与KL散度聚类损失联合优化。

考虑到k-Means方法在基于表示学习的聚类中应用广泛，许多研究还探索了在基于重构的学习中构建“k-Means友好”空间的技术。例如，DCN[248]同时优化重构目标和k-Means目标；但传统k-Means损失设计不可微，导致交替随机优化策略的复杂性增加。为解决这一问题，CKM[68]引入带具体梯度（concrete gradients）的深度k-Means策略，同时优化自编码器参数和簇质心。

在“k-Means友好”表示学习的概念基础上，研究者还探索了在潜在空间中加入其他约束以提升聚类性能的可能性：VaDE[106]探索了VAE与高斯混合模型（GMM）的结合，不仅学习到适用于聚类的优良表示，还借助混合高斯（MoG）先验增强了样本生成能力；此外，部分研究还利用自组织映射（SOM）的设计优势——SOM-VAE[61]和T-DPSOM[165]通过联合优化传统VAE和自组织映射（SOM），设计了“SOM友好”的表示学习框架，得益于学习到的潜在空间的拓扑结构和平滑性，大幅提升了时间序列表示学习的可解释性。

随着各类深度学习技术的不断涌现，不同模型设计的影响成为近年来的研究焦点之一（如图神经网络、注意力机制神经网络）：SDCN[29]提出双自监督学习框架，通过融入GCN模块的图结构信息，实现传统自编码器与图神经网络之间的知识传递，以进行统一表示学习；由于注意力机制网络已成为自然语言处理、计算机视觉等多个领域的最先进骨干架构，越来越多的研究者开始探索其在时间序列表示学习中的潜力——DeTSEC[96]首次在传统循环自编码器中引入注意力和门控机制，为适配聚类任务，在第二阶段加入聚类优化过程；TST[258]提出首个用于多变量时间序列分析的Transformer基网络，在无监督预训练阶段强制模型预测掩码片段的值，大量实验表明该建模方法在多种时间序列下游任务中均有效。

7.3.2 基于预测的学习

与基于重构的学习类似，基于预测的学习（FCST）模型也以时间序列数据为输入，生成合成数据作为输出；但两者的核心区别在于：基于重构的学习通过重构数据学习表示，而基于预测的学习通过学习过去与未来的关系来预测下一步（图20）。在该类方法的一个简单场景中，给定时间步0到 $t - 1$ 的子序列，模型预测时间步 $t$ 的值 $\hat{x}_t$ ，并基于预测值与真实数据 $x_t$ 的误差计算回归损失（式35）。需注意的是，根据预测范围的不同，回归目标函数的设计可能存在差异，但核心思想保持一致。

$\mathcal{L}_{FCST} = \left\| \hat{x}_t - x_t \right\| \tag{35}$
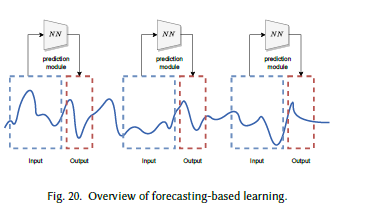
在这里插入图片描述

图20 基于预测的学习概述

近年来，研究者开始深入探索这类学习策略在时间序列分析中的应用：IT-TSC[246]设计了多路径神经网络，用于捕捉变量关联图——其中每条路径对应一个簇；给定子序列 $X(*, t_1: t_{n-1})$ ，模型通过自回归方式预测 $X(*, t_n)$ ，所有模块通过最小化回归误差进行联合优化；在推理阶段，将回归误差最小的路径分配为簇标签。

DTSS[93]提出融合时间卷积网络（TCN）和嵌入草图（embedding sketching）的混合框架，同时捕捉局部和全局特征信息：首先通过基于预测的学习策略训练嵌入空间；为进一步降维，通过滑动窗口在嵌入空间上提取草图；最后，将草图序列拼接，用于后续聚类。

表8 基于表示学习的聚类方法汇总

方法名称	二级分类	策略（Strategy）	骨干网络（Backbone）	标签（Label）	维度（Dim）
DEC [244]	基于比较（Comparative-based）	分类（CLS）	自编码器（AE）	无监督（U）*	单变量（I）*
ClusterGAN [70]	基于比较（Comparative-based）	对抗（ADV）	生成对抗网络（GAN）	无监督（U）	多变量（M）*
TCGAN [92]	基于比较（Comparative-based）	对抗（ADV）	生成对抗网络（GAN）	无监督（U）	多变量（M）
T-Loss [63]	基于比较（Comparative-based）	对比（CNRV）	卷积神经网络（CNN）	无监督（U）	多变量（M）
TS2Vec [256]	基于比较（Comparative-based）	对比（CNRV）	卷积神经网络（CNN）	无监督（U）	多变量（M）
SleepPriorCL [259]	基于比较（Comparative-based）	对比（CNRV）	卷积神经网络（CNN）	无监督（U）	多变量（M）
TF-C [264]	基于比较（Comparative-based）	对比（CNRV）	卷积神经网络（CNN）	无监督（U）	多变量（M）
BTSF [251]	基于比较（Comparative-based）	对比（CNRV）	卷积神经网络（CNN）	无监督（U）	多变量（M）
MHCCL [168]	基于比较（Comparative-based）	对比（CNRV）	卷积神经网络（CNN）	无监督（U）	多变量（M）
Ts2DEC [98]	基于比较（Comparative-based）	对比（CNRV）	卷积神经网络（CNN）	半监督（Se）*	单变量（I）
DCRLS [243]	基于比较（Comparative-based）	对比（CNRV）	卷积神经网络（CNN）	无监督（U）	多变量（M）
CROCS [122]	基于比较（Comparative-based）	对比（CNRV）	卷积神经网络（CNN）	特定（S）	单变量（I）
LDVR [9]	基于比较（Comparative-based）	对比（CNRV）	卷积神经网络（CNN）	无监督（U）	单变量（I）
RDDC [228]	基于比较（Comparative-based）	分类（CLS）	循环神经网络（RNN）	无监督（U）	多变量（M）
TSTCC [56]	基于比较（Comparative-based）	对比（CNRV）	Transformer（TRAN）	无监督（U）	多变量（M）
PCL [138]	基于比较（Comparative-based）	对比（CNRV）	卷积神经网络（CNN）	无监督（U）	多变量（M）
CCL [210]	基于比较（Comparative-based）	对比（CNRV）	卷积神经网络（CNN）	无监督（U）	多变量（M）
CRLI [158]	基于比较（Comparative-based）	对抗（ADV）	生成对抗网络（GAN）	无监督（U）	多变量（M）
TS-CTS [38]	基于比较（Comparative-based）	对比（CNRV）	卷积神经网络（CNN）	半监督（Se）	多变量（M）
TNC [226]	基于比较（Comparative-based）	对比（CNRV）	卷积神经网络（CNN）	无监督（U）	多变量（M）
IDEC [83]	基于生成（Generative-based）	重构（REC）	自编码器（AE）	无监督（U）	单变量（I）
DEPICT [71]	基于生成（Generative-based）	重构（REC）	自编码器（AE）	无监督（U）	单变量（I）
DCN [248]	基于生成（Generative-based）	重构（REC）	自编码器（AE）	无监督（U）	多变量（M）
CKM [68]	基于生成（Generative-based）	重构（REC）	自编码器（AE）	无监督（U）	单变量（I）
SOM-VAE [61]	基于生成（Generative-based）	重构（REC）	变分自编码器（VAE）	无监督（U）	单变量（I）
SDCN [29]	基于生成（Generative-based）	重构（REC）	图卷积网络（GCN）	无监督（U）	单变量（I）
DTCR [160]	基于生成（Generative-based）	重构（REC）	循环神经网络（RNN）	无监督（U）	单变量（I）
DTC [162]	基于生成（Generative-based）	重构（REC）	长短期记忆网络（LSTM）	无监督（U）	单变量（I）
VADE [106]	基于生成（Generative-based）	证据下界（ELBO）	变分自编码器（VAE）	无监督（U）	单变量（I）
TST [258]	基于生成（Generative-based）	重构（REC）	Transformer（TRAN）	无监督（U）	多变量（M）
KMRL [111]	基于生成（Generative-based）	重构（REC）	长短期记忆网络（LSTM）	无监督（U）	单变量（I）
T-DPSOM [165]	基于生成（Generative-based）	重构（REC）	长短期记忆网络（LSTM）	无监督（U）	单变量（I）
DTSS [93]	基于生成（Generative-based）	预测（FCST）	时间卷积网络（TCN）	无监督（U）	多变量（M）
DeTSEC [96]	基于生成（Generative-based）	重构（REC）	门控循环单元（GRU）	无监督（U）	多变量（M）
IT-TSC [246]	基于生成（Generative-based）	预测（FCST）	时间卷积网络（TCN）	无监督（U）	多变量（M）
DTCC [266]	混合（Hybrid-based）*	重构+对比（REC+CNRV）	长短期记忆网络（LSTM）	无监督（U）	单变量（I）
TimeCLR [252]	混合（Hybrid-based）	重构+对比（REC+CNRV）	卷积神经网络（CNN）	无监督（U）	单变量（I）
conDetSEC [97]	混合（Hybrid-based）	重构+对比（REC+CNRV）	卷积神经网络（CNN）	半监督（Se）	多变量（M）
MCAE [247]	混合（Hybrid-based）	重构+对比（REC+CNRV）	长短期记忆网络（LSTM）	无监督（U）	多变量（M）
GPT4TS [223]	基础模型（Foundation-Model）	无指定（/）	大语言模型（LLM）	无监督（U）	多变量（M）
Chronos [12]	基础模型（Foundation-Model）	预测（FCST）	大语言模型（LLM）	无监督（U）	单变量（I）
MOMENT [78]	基础模型（Foundation-Model）	重构（REC）	Transformer（TRAN）	无监督（U）	单变量（I）
TimesFM [48]	基础模型（Foundation-Model）	预测（FCST）	大语言模型（LLM）	无监督（U）	多变量（M）
UniTS [69]	基础模型（Foundation-Model）	重构（REC）	任意（*）	无监督（U）	多变量（M）

注：I：单变量，M：多变量；Se：半监督，U：无监督，S：特定标签；*：任意模型骨干/无指定策略；Hybrid-based：同时采用基于比较和基于生成两类学习策略的方法；Foundation-Model：基于基础模型的方法。

8 评估方法

本章探讨聚类评估算法——这类算法作为指标，帮助研究者评估聚类算法的有效性并选择适用方法。根据是否需要外部信息[3]，聚类评估指标通常分为两类：外部指标和内部指标。具体而言，外部指标依赖外部资源（如类别标签、真值）评估聚类结果，内部指标则基于聚类算法生成结果的固有结构进行评估。下文将在8.1节和8.2节中，详细探讨这两类指标的概念及代表性评估方法。

8.1 外部指标

如文献[3]所述，外部指标通过与外部标准（如类别标签、真值）比较，评估聚类算法生成的簇与外部标准的相似度，是目前最常用的聚类性能评估方法。

8.1.1 纯度（Purity）

获取真值簇和生成簇后，为计算生成簇相对于真值的纯度，需先根据每个生成簇内的多数类别标签，为该生成簇分配一个类别；然后，将正确分配的数据点总数除以数据点总数，得到纯度。纯度的计算公式如下（式36）：

$\frac{1}{N} \sum_{i} \max_{j} \left| C_i \cap T_j \right| \tag{36}$

其中， $N$ 表示时间序列数据点的总数， $C_i$ 表示第 $i$ 个生成簇， $T_j$ 表示第 $j$ 个真值类别标签。纯度的取值范围为0~1：聚类效果差时纯度接近0，完美聚类时纯度为1。但需注意，当簇数量多且每个簇仅含少量数据点时，易获得高纯度——例如，极端情况下每个簇仅含1个数据点，纯度为1。因此，不能仅依赖纯度评估聚类质量。

8.1.2 兰德指数（Rand Index, RI）

兰德指数由文献[195]提出。给定 $N$ 个数据点的集合 $\{x_0, x_1, \cdots, x_{N-1}\}$ ，以及基于同一数据生成的两个聚类结果（预测聚类 $\{C_0, C_1, \cdots, C_{K-1}\}$ 和真值聚类 $\{T_0, T_1, \cdots, T_{M-1}\}$ ），RI通过“相似分配数据点对数量与总数据点对数量的比值”评估 $C$ 与 $T$ 的相似度。RI的计算公式如下：

$\frac{TP + TN}{TP + TN + FP + FN}$

其中：

真阳性（TP）：数据点对在 $C$ 和 $T$ 中均被归为同一簇的次数；
真阴性（TN）：数据点对在 $C$ 和 $T$ 中均被归为不同簇的次数；
假阳性（FP）：数据点对在 $C$ 中被归为同一簇、但在 $T$ 中被归为不同簇的次数；
假阴性（FN）：数据点对在 $C$ 中被归为不同簇、但在 $T$ 中被归为同一簇的次数。

RI的取值范围为0~1： $R I = 1$ 表示两个聚类完全一致， $R I = 0$ 表示两个聚类完全不同。

8.1.3 调整兰德指数（Adjusted Rand Index, ARI）

调整兰德指数由文献[94]提出，是对兰德指数的修正——修正了“随机聚类可能导致较高/较低RI值”的问题。对于基于同一数据集生成的两个随机聚类，RI可能出现非零值，但ARI会将随机聚类的结果修正为0。ARI的计算公式如下：

$\frac{RI - Expected\ RI}{Maximum\ RI - Expected\ RI}$

ARI的取值范围为-1~1：

$A R I = 1$ ：两个聚类完全一致；
$A R I > 0$ ：两个聚类的相似度优于随机水平；
$A R I = 0$ ：两个聚类的一致性与随机水平相当；
$A R I < 0$ ：两个聚类的一致性劣于随机水平。

8.1.4 归一化互信息（Normalized Mutual Information, NMI）

NMI[219]是信息论和数据分析中广泛使用的指标，用于评估两个聚类之间的相关性或互信息。给定基于同一数据集 $X$ 的两个聚类 $M$ 和 $N$ （簇数量可不同），NMI通过计算聚类间的互信息并结合簇大小和数据点总数进行归一化，实现对 $M$ 和 $N$ 的比较。根据文献[219, 218]，NMI的计算公式如下：

$\frac{I(M;N)}{\sqrt{H(M) \cdot H(N)}} \tag{39}$
$\tag{40}$
$-\sum_{m \in M} P(m) \log_2 P(m) \tag{41}$
$-\sum_{n \in N} P(n) \log_2 P(n) \tag{42}$
$-\sum_{m \in M, n \in N} P(m,n) \log_2 \frac{P(m,n)}{P(m)} \tag{43}$

其中， $P (m, n)$ 表示聚类 $M$ 取值为 $m$ 且聚类 $N$ 取值为 $n$ 的联合概率， $P (m)$ 和 $P (n)$ 分别表示聚类 $M$ 取值为 $m$ 、聚类 $N$ 取值为 $n$ 的边缘概率。NMI的取值范围为0~1： $NM I = 1$ 表示两个聚类完全相关， $NM I = 0$ 表示两个聚类无互信息。

除上述方法外，还有其他常用外部指标可用于聚类结果评估：

F度量（F-measure）[8]：结合精确率（Precision）和召回率（Recall），取两者的调和均值，取值范围0~1，分数越高表示性能越好；
簇熵（Entropy of a cluster）[8]：评估簇内数据的杂质水平，取值范围0~1，分数越高表示簇内数据不确定性越高；
调整互信息（Adjusted Mutual Information, AMI）[167]：对互信息（MI）的修正，解决了“簇数量越多MI越高”的问题，取值范围0~1，1表示聚类完全一致。

8.2 内部指标

如文献[3]所述，内部指标与外部指标的核心区别在于：内部指标无需外部资源，仅基于聚类结果的固有结构评估聚类质量和性能。

8.2.1 轮廓系数（Silhouette Coefficient）

轮廓系数[204]是经典的内部指标之一，无需真值即可评估聚类算法的聚类结果质量。对于数据集中的单个数据点 $i$ ，其轮廓系数 $s (i)$ 的计算公式如下：

$\frac{b(i) - a(i)}{\max \{a(i), b(i)\}}$

其中：

$a (i)$ ：数据点 $i$ 与同一簇内其他所有数据点的平均距离；
$b (i)$ ：数据点 $i$ 与不同簇内数据点的最小平均距离。

单个数据点 $i$ 的 $s (i)$ 取值范围为-1~1： $s (i)$ 接近1表示 $i$ 聚类效果好，接近-1表示 $i$ 聚类效果差。整体轮廓分数为所有数据点轮廓系数的平均值：分数越高表示数据点聚类效果越好，分数极低则表示聚类不准确。

8.2.2 戴维斯-布尔丁指数（Davies-Bouldin Index, DB指数）

DB指数[49]同时考虑簇内离散度和簇间分离度，评估聚类质量，是另一种代表性内部指标。簇 $C_i$ 的离散度 $S (i)$ 定义为簇内每个点 $\in C_i$ 与其质心 $c_i$ 的平均距离，计算公式如下（式44）：

$\frac{1}{\left| C_i \right|} \sum_{x \in C_i} d\left(x, c_i\right) \tag{44}$

簇 $C_i$ 与 $C_j$ 的分离度通过两簇质心 $c_i$ 与 $c_j$ 的距离衡量，计算公式如下（式46）：

$d\left(c_i, c_j\right) \tag{46}$

获取簇内离散度和簇间分离度后，对于生成 $K$ 个簇的聚类结果，DB指数的计算公式如下（式47）：

$\frac{1}{K} \sum_{i=1}^K \max_{j=1\cdots K, j \neq i} \frac{S(i) + S(j)}{M(i,j)} \tag{47}$

DB指数的分数越低，说明每个簇的内部相似性越高，且与其他簇的区分度越好。

8.2.3 邓恩指数（Dunn Index, DI）

邓恩指数[52]是经典内部指标，计算时需考虑簇内紧致性和簇间分离度。对于 $K$ 个簇，邓恩指数的计算公式如下（式48）：

$\frac{\min_{i=1,\cdots,K, j=1,\cdots,K, i \neq j} \left\{ dist\left(C_i, C_j\right) \right\}}{\max_{p=1,\cdots,K} \left\{ diam\left(C_p\right) \right\}} \tag{48}$
$dist(C_i,C_j) = \min_{x \in C_i, y \in C_j} \left\| x - y \right\| \tag{49}$
$diam(C_p) = \max_{x,y \in C_p} \left\| x - y \right\| \tag{50}$

其中， $C_i$ 表示第 $i$ 个簇， $dist(C_i,C_j)$ 表示两簇间的最小距离（簇 $C_i$ 中某点与簇 $C_j$ 中某点的最小欧氏距离）， $diam(C_p)$ 表示簇 $C_p$ 的直径（簇内任意两点的最大欧氏距离）。邓恩指数分数越高，说明簇内紧致性越好且簇间分离度越高。但需注意，邓恩指数对异常值敏感，且计算复杂度较高。

8.2.4 簇内平方和（Within-cluster Sum of Squares, WCSS）

WCSS[161]是重要的内部指标，用于评估簇内凝聚力（簇内对象的相似程度）。WCSS通过计算每个数据点 $x$ 与其所属簇质心的平方距离之和得到，计算公式如下（式51）：

$\sum_{i=1}^K \sum_{x \in C_i} d\left(x, c_i\right)^2 \tag{51}$

其中， $K$ 表示簇数量， $c_i$ 表示第 $i$ 个簇 $C_i$ 的质心。此外，WCSS还可用于“肘部法则（elbow method）”，帮助确定需要输入簇数量的聚类算法的最优簇数 $K^*$ 。通过WCSS评估聚类结果时，分数越低表示簇内数据围绕质心的聚集程度越高；但需注意，选择过大的 $K$ 会导致WCSS极低——例如，当 $K$ 等于数据点数量时，WCSS为0。

9 结论

时间序列聚类是一种无监督任务，将相似时间序列数据聚合为组，目标是最小化类内距离、最大化类间距离。本文综述了100多种时间序列聚类算法，将其分为4个一级类别：基于距离的方法、基于分布的方法、基于子序列的方法和基于表示学习的方法；为进一步细化分类，从每个一级类别中衍生出10个二级类别，并基于该分类体系，深入探讨了每个类别中的关键算法。此外，基于以往研究[3]，本文还研究了用于评估聚类结果的外部指标和内部指标。

尽管该领域已取得数十年进展，时间序列聚类仍面临挑战。在实际场景中，当时间序列的变形无法通过预处理策略轻易消除时[178, 250, 256, 257]，不同的聚类设计变得至关重要：

划分式聚类方法（从经典k-Means开始）在聚类准确性和运行时间之间取得了良好平衡[101, 178]；
层次式聚类方法则在聚类分辨率上更具灵活性[101, 109, 157]——例如，可在树状图（dendrogram）的不同高度切割，获得更细或更粗的聚类结果。

如前文所述，相异度度量和表示方法的选择对聚类算法的准确性和运行时间起关键作用。研究者已从不同角度提出多种方法，将新见解融入这两个关键组件：

基于分布的方法聚焦于时间序列数据的分布建模，例如训练数据的隐马尔可夫模型（HMM）[134, 171]或原始时间序列空间的密度[41, 58]；
基于子序列的方法则利用代表性子序列表示每条时间序列，由于聚焦于显著模式，对噪声干扰具有鲁棒性[200, 257]。

随着深度学习技术的发展，多种基于表示学习的方法被引入该领域，并展现出有效性[63, 130, 168, 256]——这些无监督学习方法在降维和表示能力方面均表现出优异性能[130, 256]。

为揭示该领域的研究现状，已有多项评估研究受到关注：

文献[101]首次提出时间序列聚类基准，包含8种来自划分式、层次式和基于密度类别的主流方法；
尽管新提出的聚类方法数量稳步增长，但尚无单一方法能在所有数据集上表现最优；
文献[130]对深度学习基聚类方法的模型架构、学习策略和参数设置的有效性进行了全面研究，为该方向提供了参考；
文献[184]提出名为Odyssey的模块化网络引擎，支持在128个时间序列数据集上进行严格评估。

总体而言，目前尚无在所有场景下均表现最优的单一方法，这凸显了未来研究中跨领域深入探索的必要性。关键问题在于如何在不同场景下平衡聚类准确性和运行成本。本文旨在全面探索该领域，为未来时间序列聚类算法的设计提供参考。

References
[1] Tatiana Afanasieva, N Yarushkina, and Ivan Sibirev. 2017. Time series clustering using numerical and fuzzy representations. In 2017 Joint 17th World Congress of International Fuzzy Systems Association and 9th International Conference on Soft Computing and Intelligent Systems (IFSA-SCIS). IEEE, 1–7.
[2] Saeed Aghabozorgi, Mahmoud Reza Saybani, and Teh Ying Wah. 2012. Incremental clustering of time-series by fuzzy clustering. Journal of Information Science and Engineering 28, 4 (2012), 671–688.
[3] Saeed Aghabozorgi, Ali Seyed Shirkhorshidi, and Teh Ying Wah. 2015. Time-series clustering–a decade review. Information Systems 53 (2015), 16–38.
[4] Saeed Aghabozorgi and Ying Wah Teh. 2014. Stock market co-movement assessment using a three-phase clustering method. Expert Systems with Applications 41, 4 (2014), 1301–1314.
[5] Saeed Aghabozorgi, Teh Ying Wah, Tutut Herawan, Hamid A Jalab, Mohammad Amin Shaygan, and Alireza Jalali. 2014. A hybrid algorithm for clustering of time series data based on affinity search technique. The Scientific World Journal 2014 (2014).
[6] Rakesh Agrawal, Christos Faloutsos, and Arun Swami. 1993. Efficient similarity search in sequence databases. In International conference on foundations of data organization and algorithms. Springer, 69–84.
[7] Ali Alqahtani, Mohammed Ali, Xianghua Xie, and Mark W Jones. 2021. Deep time-series clustering: A review. Electronics 10, 23 (2021), 3001.
[8] Enrique Amigó, Julio Gonzalo, Javier Artiles, and Felisa Verdejo. 2009. A comparison of extrinsic clustering evaluation metrics based on formal constraints. Information retrieval 12 (2009), 461–486.
[9] Gaurangi Anand and Richi Nayak. 2020. Unsupervised visual time-series representation learning and clustering. In Neural Information Processing: 27th International Conference, ICONIP 2020, Bangkok, Thailand, November 18–22, 2020, Proceedings, Part V 27. Springer, 832–840.
[10] Henrik André-Jönsson and Dushan Z Badal. 1997. Using signature files for querying time-series data. In Principles of Data Mining and Knowledge Discovery: First European Symposium, PKDD’97 Trondheim, Norway, June 24–27, 1997 Proceedings 1. Springer, 211–220.
[11] Mihael Ankerst, Markus M Breunig, Hans-Peter Kriegel, and Jörg Sander. 1999. OPTICS: Ordering points to identify the clustering structure. ACM Sigmod record 28, 2 (1999), 49–60.
[12] Abdul Fatir Ansari, Lorenzo Stella, Caner Turkmen, Xiyuan Zhang, Pedro Mercado, Huibin Shen, Oleksandr Shchur, Syama Syndar Rangapuram, Sebastian Pineda Arango, Shubham Kapoor, Jasper Zschiegner, Danielle C. Maddix, Michael W. Mahoney, Kari Torkkola, Andrew Gordon Wilson, Michael Bohlke-Schneider, and Yuyang Wang. 2024. Chronos: Learning the Language of Time Series. Transactions on Machine Learning Research (2024). https://openreview.net/forum?id=gerNCVqqtR
[13] David Arthur and Sergei Vassilvitskii. 2007. K-means++ the advantages of careful seeding. In Proceedings of the eighteenth annual ACM-SIAM symposium on Discrete algorithms. 1027–1035.
[14] Anthony Bagnall, Hoang Anh Dau, Jason Lines, Michael Flynn, James Large, Aaron Bostrom, Paul Southam, and Eamonn Keogh. 2018. The UEA multivariate time series classification archive, 2018. arXiv preprint arXiv:1811.00075 (2018).
[15] Anthony Bagnall and Gareth Janacek. 2005. Clustering time series with clipped data. Machine learning 58, 2 (2005), 151–178.
[16] Dzmitry Bahdanau, Kyunghyun Cho, and Yoshua Bengio. 2014. Neural machine translation by jointly learning to align and translate. arXiv preprint arXiv:1409.0473 (2014).
[17] Dana H Ballard. 1987. Modular learning in neural networks. In Proceedings of the sixth National Conference on artificial intelligence-volume 1. 279–284.
[18] Mohini Bariya, Alexandra von Meier, John Paparrizos, and Michael J Franklin. 2021. k-shapestream: Probabilistic streaming clustering for electric grid events. In 2021 IEEE Madrid PowerTech. IEEE, 1–6.
[19] Ildar Batyrshin. 2013. Constructing time series shape association measures: Minkowski distance and data standardization. In 2013 BRICS congress on computational intelligence and 11th Brazilian congress on computational intelligence. IEEE, 204–212.
[20] Leonard E Baum et al. 1972. An inequality and associated maximization technique in statistical estimation for probabilistic functions of Markov processes. Inequalities 3, 1 (1972), 1–8.
[21] Mustafa Gokce Baydogan, George Runger, and Eugene Tuv. 2013. A bag-of-features framework to classify time series. IEEE transactions on pattern analysis and machine intelligence 35, 11 (2013), 2796–2802.
[22] Suzanna Becker. 1991. Unsupervised learning procedures for neural networks. International Journal of Neural Systems 2, 01n02 (1991), 17–33.
[23] Nurjahan Begum, Liudmila Ulanova, Jun Wang, and Eamonn Keogh. 2015. Accelerating dynamic time warping clustering with a novel admissible pruning strategy. In Proceedings of the 21th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. 49–58.
[24] Jan Beran and Guerino Mazzola. 1999. Visualizing the relationship between two time series by hierarchical smoothing models. Journal of Computational and Graphical Statistics 8, 2 (1999), 213–238.
[25] Donald J Berndt and James Clifford. 1994. Using dynamic time warping to find patterns in time series. In Proceedings of the 3rd international conference on knowledge discovery and data mining. 359–370.
[26] James C Bezdek. 2013. Pattern recognition with fuzzy objective function algorithms. Springer Science & Business Media.
[27] Christophe Biernacki, Gilles Celeux, and Gérard Govaert. 2000. Assessing a mixture model for clustering with the integrated completed likelihood. IEEE transactions on pattern analysis and machine intelligence 22, 7 (2000), 719–725.
[28] Christopher M Bishop and Nasser M Nasrabadi. 2006. Pattern recognition and machine learning. Vol. 4. Springer.
[29] Deyu Bo, XiaoWang, Chuan Shi, Meiqi Zhu, Emiao Lu, and Peng Cui. 2020. Structural deep clustering network. In Proceedings of the web conference 2020. 1400–1410.
[30] Fabrizio Bonacina, Eric Stefan Miele, and Alessandro Corsini. 2020. Time series clustering: a complex network-based approach for feature selection in multi-sensor data. Modelling 1, 1 (2020), 1–21.
[31] Paul Boniol, John Paparrizos, Yuhao Kang, Themis Palpanas, Ruey S Tsay, Aaron J Elmore, and Michael J Franklin. 2022. Theseus: navigating the labyrinth of time-series anomaly detection. Proceedings of the VLDB Endowment 15, 12 (2022), 3702–3705.
[32] Paul Boniol, John Paparrizos, and Themis Palpanas. 2023. New Trends in Time Series Anomaly Detection… In EDBT. 847–850.
[33] Paul Boniol, John Paparrizos, and Themis Palpanas. 2024. An Interactive Dive into Time-Series Anomaly Detection. In 2024 IEEE 40th International Conference on Data Engineering (ICDE).
[34] Paul Boniol, John Paparrizos, Themis Palpanas, and Michael J Franklin. 2021. Sand in action: subsequence anomaly detection for streams. Proceedings of the VLDB Endowment 14, 12 (2021), 2867–2870.
[35] Paul Boniol, John Paparrizos, Themis Palpanas, and Michael J Franklin. 2021. SAND: streaming subsequence anomaly detection. Proceedings of the VLDB Endowment 14, 10 (2021), 1717–1729.
[36] Paul Boniol, Emmanouil Sylligardos, John Paparrizos, Panos Trahanias, and Themis Palpanas. 2024. ADecimo: Model Selection for Time Series Anomaly Detection. In 2024 IEEE 40th International Conference on Data Engineering (ICDE).
[37] Kin-Pong Chan and Ada Wai-Chee Fu. 1999. Efficient time series matching by wavelets. In Proceedings 15th International Conference on Data Engineering (Cat. No. 99CB36337). IEEE, 126–133.
[38] Yuan-Chi Chang, Dharmashankar Subramanian, Raju Pavuluri, and Timothy Dinger. 2022. Time series representation learning with contrastive triplet selection. In 5th Joint International Conference on Data Science & Management of Data (9th ACM IKDD CODS and 27th COMAD). 46–53.
[39] Ting Chen, Simon Kornblith, Mohammad Norouzi, and Geoffrey Hinton. 2020. A simple framework for contrastive learning of visual representations. In International conference on machine learning. PMLR, 1597–1607.
[40] Yanping Chen, Eamonn Keogh, Bing Hu, Nurjahan Begum, Anthony Bagnall, Abdullah Mueen, and Gustavo Batista. 2015. The UCR Time Series Classification Archive. www.cs.ucr.edu/~eamonn/time_series_data/.
[41] Yixin Chen and Li Tu. 2007. Density-based clustering for real-time stream data. In Proceedings of the 13th ACM SIGKDD international conference on Knowledge discovery and data mining. 133–142.
[42] Kyunghyun Cho, Bart Van Merriënboer, Caglar Gulcehre, Dzmitry Bahdanau, Fethi Bougares, Holger Schwenk, and Yoshua Bengio. 2014. Learning phrase representations using RNN encoder-decoder for statistical machine translation. arXiv preprint arXiv:1406.1078 (2014).
[43] Kushan Ajay Choksi, Sonal Jain, and Naran M Pindoriya. 2020. Feature based clustering technique for investigation of domestic load profiles and probabilistic variation assessment: Smart meter dataset. Sustainable Energy, Grids and Networks 22 (2020), 100346.
[44] Maximilian Christ, Nils Braun, Julius Neuffer, and Andreas W Kempa-Liehr. 2018. Time series feature extraction on basis of scalable hypothesis
tests (tsfresh–a python package). Neurocomputing 307 (2018), 72–77.
[45] Maximilian Christ, Andreas W Kempa-Liehr, and Michael Feindt. 2016. Distributed and parallel time series feature extraction for industrial big
data applications. arXiv preprint arXiv:1610.07717 (2016).
[46] Selina Chu, Eamonn Keogh, David Hart, and Michael Pazzani. 2002. Iterative deepening dynamic time warping for time series. In Proceedings of the
2002 SIAM International Conference on Data Mining. SIAM, 195–212.
[47] Robert Darkins, Emma J Cooke, Zoubin Ghahramani, Paul DW Kirk, David L Wild, and Richard S Savage. 2013. Accelerating Bayesian hierarchical
clustering of time series data with a randomised algorithm. PloS one 8, 4 (2013), e59795.
[48] Abhimanyu Das, Weihao Kong, Rajat Sen, and Yichen Zhou. 2024. A decoder-only foundation model for time-series forecasting. In Forty-first
International Conference on Machine Learning. https://openreview.net/forum?id=jn2iTJas6h
[49] David L Davies and Donald W Bouldin. 1979. A cluster separation measure. IEEE transactions on pattern analysis and machine intelligence 2 (1979),
224–227.
[50] Rui Ding, Qiang Wang, Yingnong Dang, Qiang Fu, Haidong Zhang, and Dongmei Zhang. 2015. Yading: Fast clustering of large-scale time series
data. Proceedings of the VLDB Endowment 8, 5 (2015), 473–484.
[51] Joseph C Dunn. 1973. A fuzzy relative of the ISODATA process and its use in detecting compact well-separated clusters. (1973).
[52] Joseph C Dunn. 1974. Well-separated clusters and optimal fuzzy partitions. Journal of cybernetics 4, 1 (1974), 95–104.
[53] Adam Dziedzic, John Paparrizos, Sanjay Krishnan, Aaron Elmore, and Michael Franklin. 2019. Band-limited training and inference for convolutional
neural networks. In International Conference on Machine Learning. PMLR, 1745–1754.
[54] Jens E d’Hondt, Odysseas Papapetrou, and John Paparrizos. 2024. Beyond the Dimensions: A Structured Evaluation of Multivariate Time Series
Distance Measures. In 2024 IEEE 40th International Conference on Data Engineering Workshops (ICDEW). IEEE, 107–112.
[55] Hussein El Amouri, Thomas Lampert, Pierre Gançarski, and Clément Mallet. 2023. Constrained DTW preserving shapelets for explainable
time-Series clustering. Pattern Recognition 143 (2023), 109804.
[56] Emadeldeen Eldele, Mohamed Ragab, Zhenghua Chen, Min Wu, Chee Keong Kwoh, Xiaoli Li, and Cuntai Guan. 2021. Time-Series Representation
Learning via Temporal and Contextual Contrasting. In Proceedings of the Thirtieth International Joint Conference on Artificial Intelligence, IJCAI-21.
2352–2359.
[57] Jonatan Enes, Roberto R Expósito, José Fuentes, Javier López Cacheiro, and Juan Touriño. 2023. A pipeline architecture for feature-based
unsupervised clustering using multivariate time series from HPC jobs. Information Fusion 93 (2023), 1–20.
[58] Martin Ester, Hans-Peter Kriegel, Jörg Sander, Xiaowei Xu, et al. 1996. A density-based algorithm for discovering clusters in large spatial databases
with noise… In kdd, Vol. 96. 226–231.
[59] Carolina Euán, Hernando Ombao, and Joaquín Ortega. 2018. The hierarchical spectral merger algorithm: a new time series clustering procedure.
Journal of Classification 35 (2018), 71–99.
[60] Christos Faloutsos, Mudumbai Ranganathan, and Yannis Manolopoulos. 1994. Fast subsequence matching in time-series databases. ACM Sigmod
Record 23, 2 (1994), 419–429.
[61] Vincent Fortuin, Matthias Hüser, Francesco Locatello, Heiko Strathmann, and Gunnar Rätsch. 2019. Deep Self-Organization: Interpretable Discrete
Representation Learning on Time Series. In International Conference on Learning Representations. https://openreview.net/forum?id=rygjcsR9Y7
[62] Vanel Steve Siyou Fotso, Engelbert Mephu Nguifo, and Philippe Vaslin. 2020. Frobenius correlation based u-shapelets discovery for time series
clustering. Pattern Recognition 103 (2020), 107301.
[63] Jean-Yves Franceschi, Aymeric Dieuleveut, and Martin Jaggi. 2019. Unsupervised scalable representation learning for multivariate time series.
Advances in neural information processing systems 32 (2019).
[64] Tak-chung Fu, Fu-lai Chung, Vincent Ng, and Robert Luk. 2001. Pattern discovery from stock time series using self-organizing maps. In Workshop
Notes of KDD2001 Workshop on Temporal Data Mining, Vol. 1. Citeseer.
[65] Ben D Fulcher. 2018. Feature-based time-series analysis. In Feature engineering for machine learning and data analytics. CRC press, 87–116.
[66] Ben D Fulcher and Nick S Jones. 2014. Highly comparative feature-based time-series classification. IEEE Transactions on Knowledge and Data
Engineering 26, 12 (2014), 3026–3037.
[67] Ben D Fulcher and Nick S Jones. 2017. hctsa: A computational framework for automated time-series phenotyping using massive feature extraction.
Cell systems 5, 5 (2017), 527–531.
[68] Boyan Gao, Yongxin Yang, Henry Gouk, and Timothy M Hospedales. 2020. Deep clusteringwith concrete k-means. In ICASSP 2020-2020 IEEE
international conference on acoustics, speech and signal processing (ICASSP). IEEE, 4252–4256.
[69] Shanghua Gao, Teddy Koker, Owen Queen, Thomas Hartvigsen, Theodoros Tsiligkaridis, and Marinka Zitnik. 2024. UniTS: Building a Unified
Time Series Model. arXiv (2024). https://arxiv.org/pdf/2403.00131.pdf
[70] Kamran Ghasedi, Xiaoqian Wang, Cheng Deng, and Heng Huang. 2019. Balanced self-paced learning for generative adversarial clustering network.
In Proceedings of the IEEE/CVF conference on computer vision and pattern recognition. 4391–4400.
[71] Kamran Ghasedi Dizaji, Amirhossein Herandi, Cheng Deng, Weidong Cai, and Heng Huang. 2017. Deep clustering via joint convolutional
autoencoder embedding and relative entropy minimization. In Proceedings of the IEEE international conference on computer vision. 5736–5745.
[72] Shima Ghassempour, Federico Girosi, and Anthony Maeder. 2014. Clustering multivariate time series using hidden Markov models. International
journal of environmental research and public health 11, 3 (2014), 2741–2763.
[73] Rafael Giusti and Gustavo EAPA Batista. 2013. An empirical comparison of dissimilarity measures for time series classification. In 2013 Brazilian
Conference on Intelligent Systems. IEEE, 82–88.
[74] Rahul Goel, Sandeep Soni, Naman Goyal, John Paparrizos, Hanna Wallach, Fernando Diaz, and Jacob Eisenstein. 2016. The social dynamics of
language change in online networks. In Social Informatics: 8th International Conference, SocInfo 2016, Bellevue, WA, USA, November 11-14, 2016,
Proceedings, Part I 8. Springer, 41–57.
[75] Xavier Golay, Spyros Kollias, Gautier Stoll, Dieter Meier, Anton Valavanis, and Peter Boesiger. 1998. A new correlation-based fuzzy logic clustering
algorithm for FMRI. Magnetic resonance in medicine 40, 2 (1998), 249–260.
[76] Gene H Golub and Charles F Van Loan. 2013. Matrix computations. JHU press.
[77] Ian Goodfellow, Jean Pouget-Abadie, Mehdi Mirza, Bing Xu, DavidWarde-Farley, Sherjil Ozair, Aaron Courville, and Yoshua Bengio. 2014. Generative
Adversarial Nets. In Advances in Neural Information Processing Systems, Z. Ghahramani, M. Welling, C. Cortes, N. Lawrence, and K.Q. Weinberger
(Eds.), Vol. 27. Curran Associates, Inc. https://proceedings.neurips.cc/paper_files/paper/2014/file/5ca3e9b122f61f8f06494c97b1afccf3-Paper.pdf
[78] Mononito Goswami, Konrad Szafer, Arjun Choudhry, Yifu Cai, Shuo Li, and Artur Dubrawski. 2024. MOMENT: A Family of Open Time-series
Foundation Models. In International Conference on Machine Learning.
[79] He-Shan Guam and Qing-Shan Jiang. 2007. Cluster financial time series for portfolio. In 2007 international conference on wavelet analysis and
pattern recognition, Vol. 2. IEEE, 851–856.
[80] David Guijo-Rubio, Antonio Manuel Durán-Rosal, Pedro Antonio Gutiérrez, Alicia Troncoso, and César Hervás-Martínez. 2020. Time-series
clustering based on the characterization of segment typologies. IEEE transactions on cybernetics 51, 11 (2020), 5409–5422.
[81] Francesco Gullo, Giovanni Ponti, Andrea Tagarelli, Giuseppe Tradigo, and Pierangelo Veltri. 2012. A time series approach for clustering mass
spectrometry data. Journal of Computational Science 3, 5 (2012), 344–355.
[82] Chonghui Guo, Hongfeng Jia, and Na Zhang. 2008. Time series clustering based on ICA for stock data analysis. In 2008 4th international conference
on wireless communications, networking and mobile computing. IEEE, 1–4.
[83] Xifeng Guo, Long Gao, Xinwang Liu, and Jianping Yin. 2017. Improved Deep Embedded Clustering with Local Structure Preservation… In IJCAI.
1753–1759.
[84] Will Hamilton, Zhitao Ying, and Jure Leskovec. 2017. Inductive representation learning on large graphs. Advances in neural information processing
systems 30 (2017).
[85] Kaiming He, Xiangyu Zhang, Shaoqing Ren, and Jian Sun. 2016. Deep residual learning for image recognition. In Proceedings of the IEEE conference
on computer vision and pattern recognition. 770–778.
[86] Alexander Hinneburg and Hans-Henning Gabriel. 2007. Denclue 2.0: Fast clustering based on kernel density estimation. In International symposium
on intelligent data analysis. Springer, 70–80.
[87] Alexander Hinneburg and Daniel A Keim. 1998. An efficient approach to clustering in large multimedia databases with noise. In Knowledge
Discovery and Datamining (KDD’98). 58–65.
[88] Sepp Hochreiter and Jürgen Schmidhuber. 1997. Long short-term memory. Neural computation 9, 8 (1997), 1735–1780.
[89] Christopher Holder, Matthew Middlehurst, and Anthony Bagnall. 2023. A review and evaluation of elastic distance functions for time series
clustering. Knowledge and Information Systems (2023), 1–45.
[90] John J Hopfield. 1982. Neural networks and physical systems with emergent collective computational abilities. Proceedings of the national academy
of sciences 79, 8 (1982), 2554–2558.
[91] Maomao Hu, Dongjiao Ge, Rory Telford, Bruce Stephen, and David CH Wallom. 2021. Classification and characterization of intra-day load curves
of PV and non-PV households using interpretable feature extraction and feature-based clustering. Sustainable Cities and Society 75 (2021), 103380.
[92] Fanling Huang and Yangdong Deng. 2023. TCGAN: Convolutional Generative Adversarial Network for time series classification and clustering.
Neural Networks 165 (2023), 868–883.
[93] Hao Huang, Tapan Shah, and Shinjae Yoo. 2022. Deep Time Series Sketching and Its Application on Industrial Time Series Clustering. In 2022 IEEE
International Conference on Big Data (Big Data). IEEE, 1997–2006.
[94] Lawrence Hubert and Phipps Arabie. 1985. Comparing partitions. Journal of classification 2 (1985), 193–218.
[95] Rob J Hyndman and George Athanasopoulos. 2018. Forecasting: principles and practice. OTexts.
[96] Dino Ienco and Roberto Interdonato. 2020. Deep multivariate time series embedding clustering via attentive-gated autoencoder. In Advances
in Knowledge Discovery and Data Mining: 24th Pacific-Asia Conference, PAKDD 2020, Singapore, May 11–14, 2020, Proceedings, Part I 24. Springer,
318–329.
[97] Dino Ienco and Roberto Interdonato. 2023. Deep semi-supervised clustering for multi-variate time-series. Neurocomputing 516 (2023), 36–47.
[98] Dino Ienco and Ruggero G Pensa. 2019. Deep triplet-driven semi-supervised embedding clustering. In Discovery Science: 22nd International
Conference, DS 2019, Split, Croatia, October 28–30, 2019, Proceedings 22. Springer, 220–234.
[99] Félix Iglesias and Wolfgang Kastner. 2013. Analysis of similarity measures in times series clustering for the discovery of building energy patterns.
Energies 6, 2 (2013), 579–597.
[100] Anil K Jain and Richard C Dubes. 1988. Algorithms for clustering data. Prentice-Hall, Inc.
[101] Ali Javed, Byung Suk Lee, and Donna M Rizzo. 2020. A benchmark study on time series clustering. Machine Learning with Applications 1 (2020),
100001.
[102] Hoyoung Jeung, Sofiane Sarni, Ioannis Paparrizos, Saket Sathe, Karl Aberer, Nicholas Dawes, Thanasis G Papaioannou, and Michael Lehning.
2010. Effective metadata management in federated sensor networks. In 2010 IEEE International Conference on Sensor Networks, Ubiquitous, and
Trustworthy Computing. IEEE, 107–114.
[103] Min Ji, Fuding Xie, and Yu Ping. 2013. A dynamic fuzzy cluster algorithm for time series. In Abstract and Applied Analysis, Vol. 2013. Hindawi.
[104] Hao Jiang, Chunwei Liu, Qi Jin, John Paparrizos, and Aaron J Elmore. 2020. Pids: attribute decomposition for improved compression and query
performance in columnar storage. Proceedings of the VLDB Endowment 13, 6 (2020), 925–938.
[105] Hao Jiang, Chunwei Liu, John Paparrizos, Andrew A Chien, Jihong Ma, and Aaron J Elmore. 2021. Good to the last bit: Data-driven encoding with
codecdb. In Proceedings of the 2021 International Conference on Management of Data. 843–856.
[106] Zhuxi Jiang, Yin Zheng, Huachun Tan, Bangsheng Tang, and Hanning Zhou. 2017. Variational deep embedding: an unsupervised and generative
approach to clustering. In Proceedings of the 26th International Joint Conference on Artificial Intelligence. 1965–1972.
[107] CI Johnpaul, Munaga VNK Prasad, S Nickolas, and GR Gangadharan. 2020. Trendlets: A novel probabilistic representational structures for clustering
the time series data. Expert Systems with Applications 145 (2020), 113119.
[108] Eleanna Kafeza, Gerasimos Rompolas, Sokratis Kyriazidis, and Christos Makris. 2022. Time-Series Clustering for Determining Behavioral-Based
Brand Loyalty of Users Across Social Media. IEEE Transactions on Computational Social Systems (2022).
[109] Yoshihide Kakizawa, Robert H Shumway, and Masanobu Taniguchi. 1998. Discrimination and clustering for multivariate time series. J. Amer.
Statist. Assoc. 93, 441 (1998), 328–340.
[110] Konstantinos Kalpakis, Dhiral Gada, and Vasundhara Puttagunta. 2001. Distance measures for effective clustering of ARIMA time-series. In
Proceedings 2001 IEEE international conference on data mining. IEEE, 273–280.
[111] Antonina Kashtalian and Tomas Sochor. 2021. K-means Clustering of Honeynet Data with Unsupervised Representation Learning… In IntelITSIS.
439–449.
[112] Leonard Kaufman and Peter J Rousseeuw. 2009. Finding groups in data: an introduction to cluster analysis. John Wiley & Sons.
[113] Kyoji Kawagoe and Tomohiro Ueda. 2002. A similarity search method of time series data with combination of Fourier and wavelet transforms. In
Proceedings Ninth International Symposium on Temporal Representation and Reasoning. IEEE, 86–92.
[114] Eamonn Keogh, Kaushik Chakrabarti, Michael Pazzani, and Sharad Mehrotra. 2001. Dimensionality reduction for fast similarity search in large
time series databases. Knowledge and information Systems 3 (2001), 263–286.
[115] Eamonn Keogh and Jessica Lin. 2005. Clustering of time-series subsequences is meaningless: implications for previous and future research.
Knowledge and information systems 8 (2005), 154–177.
[116] Eamonn Keogh, Stefano Lonardi, and Chotirat Ann Ratanamahatana. 2004. Towards parameter-free data mining. In Proceedings of the tenth ACM
SIGKDD international conference on Knowledge discovery and data mining. 206–215.
[117] Eamonn J Keogh and Michael J Pazzani. 1998. An Enhanced Representation of Time Series Which Allows Fast and Accurate Classification,
Clustering and Relevance Feedback… In Kdd, Vol. 98. 239–243.
[118] Eamonn J Keogh and Michael J Pazzani. 2000. A simple dimensionality reduction technique for fast similarity search in large time series databases.
In Pacific-Asia conference on knowledge discovery and data mining. Springer, 122–133.
[119] Mohammad Mahmudur Rahman Khan, Md Abu Bakr Siddique, Rezoana Bente Arif, and Mahjabin Rahman Oishe. 2018. ADBSCAN: Adaptive
density-based spatial clustering of applications with noise for identifying clusters with varying densities. In 2018 4th international conference on
electrical engineering and information & communication technology (iCEEiCT). IEEE, 107–111.
[120] Diederik P Kingma and Max Welling. 2013. Auto-encoding variational bayes. arXiv preprint arXiv:1312.6114 (2013).
[121] Thomas N. Kipf and Max Welling. 2017. Semi-Supervised Classification with Graph Convolutional Networks. In International Conference on
Learning Representations. https://openreview.net/forum?id=SJU4ayYgl
[122] Dani Kiyasseh, Tingting Zhu, and David Clifton. 2021. CROCS: clustering and retrieval of cardiac signals based on patient disease class, sex, and
age. Advances in Neural Information Processing Systems 34 (2021), 15557–15569.
[123] Katarina Košmelj and Vladimir Batagelj. 1990. Cross-sectional approach for clustering time varying data. Journal of Classification 7, 1 (1990),
99–109.
[124] Mark A Kramer. 1991. Nonlinear principal component analysis using autoassociative neural networks. AIChE journal 37, 2 (1991), 233–243.
[125] Hans-Peter Kriegel and Martin Pfeifle. 2005. Density-based clustering of uncertain data. In Proceedings of the eleventh ACM SIGKDD international
conference on Knowledge discovery in data mining. 672–677.
[126] Sanjay Krishnan, Aaron J Elmore, Michael Franklin, John Paparrizos, Zechao Shang, Adam Dziedzic, and Rui Liu. 2019. Artificial intelligence in
resource-constrained and shared environments. ACM SIGOPS Operating Systems Review 53, 1 (2019), 1–6.
[127] Alex Krizhevsky, Ilya Sutskever, and Geoffrey E Hinton. 2012. Imagenet classification with deep convolutional neural networks. Advances in neural
information processing systems 25 (2012).
[128] Mahesh Kumar, Nitin R Patel, and Jonathan Woo. 2002. Clustering seasonality patterns in the presence of errors. In Proceedings of the eighth ACM
SIGKDD international conference on Knowledge discovery and data mining. 557–563.
[129] Vladimir Kurbalija, Charlotte von Bernstorff, Hans-Dieter Burkhard, Jens Nachtwei, Mirjana Ivanović, and Lidija Fodor. 2012. Time-Series Mining
in a Psychological Domain. In Proceedings of the Fifth Balkan Conference in Informatics (Novi Sad, Serbia) (BCI ’12). Association for Computing
Machinery, New York, NY, USA, 58–63. https://doi.org/10.1145/2371316.2371328
[130] Baptiste Lafabregue, Jonathan Weber, Pierre Gançarski, and Germain Forestier. 2021. End-to-end deep representation learning for time series
clustering: a comparative study. Data Mining and Knowledge Discovery (2021), 1–53.
[131] Qi Lei, Jinfeng Yi, Roman Vaculin, Lingfei Wu, and Inderjit S. Dhillon. 2019. Similarity Preserving Representation Learning for Time Series
Clustering. In Proceedings of the 28th International Joint Conference on Artificial Intelligence (Macao, China) (IJCAI’19). AAAI Press, 2845–2851.
[132] Aimin Li, Siqi Xiong, Junhuai Li, Saurav Mallik, Yajun Liu, Rong Fei, Hongfang Zhou, and Guangming Liu. 2022. AngClust: angle feature-based
clustering for short time series gene expression profiles. IEEE/ACM Transactions on Computational Biology and Bioinformatics 20, 2 (2022),
1574–1580.
[133] Cen Li and Gautam Biswas. 1999. Temporal pattern generation using hidden Markov model based unsupervised classification. In International
Symposium on Intelligent Data Analysis. Springer, 245–256.
[134] Cen Li, Gautam Biswas, Mike Dale, and Pat Dale. 2001. Building models of ecological dynamics using HMM based temporal data clustering—a
preliminary study. In International Symposium on Intelligent Data Analysis. Springer, 53–62.
[135] Guozhong Li, Byron Choi, Jianliang Xu, Sourav S Bhowmick, Kwok-Pan Chun, and Grace Lai-Hung Wong. 2021. ShapeNet: A Shapelet-Neural
Network Approach for Multivariate Time Series Classification. Proceedings of the AAAI Conference on Artificial Intelligence 35, 9 (May 2021),
8375–8383. https://doi.org/10.1609/aaai.v35i9.17018
[136] Hailin Li and Manhua Chen. 2023. Time series clustering based on normal cloud model and complex network. Applied Soft Computing 148 (2023),
110876.
[137] Hailin Li, Xianli Wu, Xiaoji Wan, and Weibin Lin. 2022. Time series clustering via matrix profile and community detection. Advanced Engineering
Informatics 54 (2022), 101771.
[138] Junnan Li, Pan Zhou, Caiming Xiong, and Steven C.H. Hoi. 2021. Prototypical Contrastive Learning of Unsupervised Representations. In ICLR.
[139] Xiaosheng Li, Jessica Lin, and Liang Zhao. 2021. Time series clustering in linear time complexity. Data Mining and Knowledge Discovery 35 (2021),
2369–2388.
[140] Xiang Li, Jinglu Wang, Xiaohao Xu, Muqiao Yang, Fan Yang, Yizhou Zhao, Rita Singh, and Bhiksha Raj. 2023. Towards Noise-Tolerant Speech-
Referring Video Object Segmentation: Bridging Speech and Text. In Proceedings of the 2023 Conference on Empirical Methods in Natural Language
Processing, Houda Bouamor, Juan Pino, and Kalika Bali (Eds.). Association for Computational Linguistics, Singapore, 2283–2296. https://doi.org/10.
18653/v1/2023.emnlp-main.140
[141] Zhiyu Liang, Jianfeng Zhang, Chen Liang, Hongzhi Wang, Zheng Liang, and Lujia Pan. 2023. Contrastive Shapelet Learning for Unsupervised
Multivariate Time Series Representation Learning. arXiv preprint arXiv:2305.18888 (2023).
[142] TW Liao, B Bolt, J Forester, E Hailman, C Hansen, RC Kaste, and J O’May. 2002. Understanding and projecting the battle state. In 23rd Army Science
Conference, Orlando, FL, Vol. 25.
[143] T Warren Liao. 2005. Clustering of time series data—a survey. Pattern recognition 38, 11 (2005), 1857–1874.
[144] Jessica Lin, Eamonn Keogh, Stefano Lonardi, and Bill Chiu. 2003. A symbolic representation of time series, with implications for streaming
algorithms. In Proceedings of the 8th ACM SIGMOD workshop on Research issues in data mining and knowledge discovery. 2–11.
[145] Jessica Lin, Eamonn Keogh, Li Wei, and Stefano Lonardi. 2007. Experiencing SAX: a novel symbolic representation of time series. Data Mining and
knowledge discovery 15, 2 (2007), 107–144.
[146] Jessica Lin, Michail Vlachos, Eamonn Keogh, and Dimitrios Gunopulos. 2004. Iterative incremental clustering of time series. In International
Conference on Extending Database Technology. Springer, 106–122.
[147] Chunwei Liu, Hao Jiang, John Paparrizos, and Aaron J Elmore. 2021. Decomposed bounded floats for fast compression and queries. Proceedings of
the VLDB Endowment 14, 11 (2021), 2586–2598.
[148] Chunwei Liu, John Paparrizos, and Aaron J Elmore. 2024. Adaedge: A dynamic compression selection framework for resource constrained devices.
In 2024 IEEE 40th International Conference on Data Engineering (ICDE). IEEE, 1506–1519.
[149] Qinghua Liu, Paul Boniol, Themis Palpanas, and John Paparrizos. 2024. Time-Series Anomaly Detection: Overview and New Trends. Proceedings of
the VLDB Endowment (PVLDB) 17, 12 (2024), 4229–4232.
[150] Qinghua Liu and John Paparrizos. 2024. The Elephant in the Room: Towards A Reliable Time-Series Anomaly Detection Benchmark. In NeurIPS
2024.
[151] Shinan Liu, Tarun Mangla, Ted Shaowang, Jinjin Zhao, John Paparrizos, Sanjay Krishnan, and Nick Feamster. 2023. Amir: Active multimodal
interaction recognition from video and network traffic in connected environments. Proceedings of the ACM on Interactive, Mobile, Wearable and
Ubiquitous Technologies 7, 1 (2023), 1–26.
[152] Arnaud Lods, Simon Malinowski, Romain Tavenard, and Laurent Amsaleg. 2017. Learning DTW-preserving shapelets. In Advances in Intelligent
Data Analysis XVI: 16th International Symposium, IDA 2017, London, UK, October 26–28, 2017, Proceedings 16. Springer, 198–209.
[153] David G Lowe. 2004. Distinctive image features from scale-invariant keypoints. International journal of computer vision 60 (2004), 91–110.
[154] Carl H Lubba, Sarab S Sethi, Philip Knaute, Simon R Schultz, Ben D Fulcher, and Nick S Jones. 2019. catch22: CAnonical Time-series CHaracteristics:
Selected through highly comparative time-series analysis. Data Mining and Knowledge Discovery 33, 6 (2019), 1821–1852.
[155] Maciej Łuczak. 2016. Hierarchical clustering of time series data with parametric derivative dynamic time warping. Expert Systems with Applications
62 (2016), 116–130.
[156] Linghao Luo and Shu Lv. 2020. An accelerated u-shapelet time series clustering method with lsh. In Journal of Physics: Conference Series, Vol. 1631.
IOP Publishing, 012077.
[157] Zhixue Luo, Lin Zhang, Na Liu, and Ye Wu. 2023. Time series clustering of COVID-19 pandemic-related data. Data Science and Management 6, 2
(2023), 79–87.
[158] Qianli Ma, Chuxin Chen, Sen Li, and Garrison W. Cottrell. 2021. Learning Representations for Incomplete Time Series Clustering. Proceedings of
the AAAI Conference on Artificial Intelligence 35, 10 (May 2021), 8837–8846. https://doi.org/10.1609/aaai.v35i10.17070
[159] Qianli Ma, Chuxin Chen, Sen Li, and Garrison W. Cottrell. 2021. Learning Representations for Incomplete Time Series Clustering. Proceedings of
the AAAI Conference on Artificial Intelligence 35, 10 (May 2021), 8837–8846. https://doi.org/10.1609/aaai.v35i10.17070
[160] Qianli Ma, Jiawei Zheng, Sen Li, and Gary W Cottrell. 2019. Learning representations for time series clustering. Advances in neural information
processing systems 32 (2019).
[161] James MacQueen et al. 1967. Some methods for classification and analysis of multivariate observations. In Proceedings of the fifth Berkeley
symposium on mathematical statistics and probability, Vol. 1. Oakland, CA, USA, 281–297.
[162] Naveen Sai Madiraju. 2018. Deep temporal clustering: Fully unsupervised learning of time-domain features. Ph.D. Dissertation. Arizona State
University.
[163] Elizabeth Ann Maharaj. 2000. Cluster of Time Series. Journal of Classification 17, 2 (2000).
[164] Simon Malinowski, Thomas Guyet, René Quiniou, and Romain Tavenard. 2013. 1d-sax: A novel symbolic representation for time series. In
International Symposium on Intelligent Data Analysis. Springer, 273–284.
[165] Laura Manduchi, Matthias Hüser, Julia Vogt, Gunnar Rätsch, and Vincent Fortuin. 2019. DPSOM: Deep probabilistic clustering with self-organizing
maps. arXiv preprint arXiv:1910.01590 (2019).
[166] Kathy McKeown, Hal Daume III, Snigdha Chaturvedi, John Paparrizos, Kapil Thadani, Pablo Barrio, Or Biran, Suvarna Bothe, Michael Collins,
Kenneth R Fleischmann, et al. 2016. Predicting the impact of scientific concepts using full-text features. Journal of the Association for Information
Science and Technology 67, 11 (2016), 2684–2696.
[167] Marina Meilă. 2007. Comparing clusterings—an information based distance. Journal of multivariate analysis 98, 5 (2007), 873–895.
[168] Qianwen Meng, Hangwei Qian, Yong Liu, Lizhen Cui, Yonghui Xu, and Zhiqi Shen. 2023. MHCCL: masked hierarchical cluster-wise contrastive
learning for multivariate time series. In Proceedings of the AAAI Conference on Artificial Intelligence, Vol. 37. 9153–9161.
[169] Tomas Mikolov, Ilya Sutskever, Kai Chen, Greg S Corrado, and Jeff Dean. 2013. Distributed representations of words and phrases and their
compositionality. Advances in neural information processing systems 26 (2013).
[170] Carla S Möller-Levet, Frank Klawonn, Kwang-Hyun Cho, and Olaf Wolkenhauer. 2003. Fuzzy clustering of short time-series and unevenly
distributed sampling points. In International symposium on intelligent data analysis. Springer, 330–340.
[171] Tim Oates, Laura Firoiu, and Paul R Cohen. 1999. Clustering time series with hidden markov models and dynamic time warping. In Proceedings of
the IJCAI-99 workshop on neural, symbolic and reinforcement learning methods for sequence learning. Citeseer, 17–21.
[172] Aaron van den Oord, Yazhe Li, and Oriol Vinyals. 2018. Representation learning with contrastive predictive coding. arXiv preprint arXiv:1807.03748
(2018).
[173] Mert Ozer, Anna Sapienza, Andrés Abeliuk, Goran Muric, and Emilio Ferrara. 2020. Discovering patterns of online popularity from time series.
Expert Systems with Applications 151 (2020), 113337.
[174] Ioannis Paparrizos. 2018. Fast, scalable, and accurate algorithms for time-series analysis. Ph.D. Dissertation. Columbia University.
[175] John Paparrizos, Paul Boniol, Themis Palpanas, Ruey S Tsay, Aaron Elmore, and Michael J Franklin. 2022. Volume under the surface: a new accuracy
evaluation measure for time-series anomaly detection. Proceedings of the VLDB Endowment 15, 11 (2022), 2774–2787.
[176] John Paparrizos, Ikraduya Edian, Chunwei Liu, Aaron J Elmore, and Michael J Franklin. 2022. Fast adaptive similarity search through variance-aware
quantization. In 2022 IEEE 38th International Conference on Data Engineering (ICDE). IEEE, 2969–2983.
[177] John Paparrizos and Michael J Franklin. 2019. Grail: efficient time-series representation learning. Proceedings of the VLDB Endowment 12, 11 (2019),
1762–1777.
[178] John Paparrizos and Luis Gravano. 2015. k-shape: Efficient and accurate clustering of time series. In Proceedings of the 2015 ACM SIGMOD
international conference on management of data. 1855–1870.
[179] John Paparrizos and Luis Gravano. 2017. Fast and accurate time-series clustering. ACM Transactions on Database Systems (TODS) 42, 2 (2017), 1–49.
[180] John Paparrizos, Yuhao Kang, Paul Boniol, Ruey S Tsay, Themis Palpanas, and Michael J Franklin. 2022. TSB-UAD: an end-to-end benchmark suite
for univariate time-series anomaly detection. Proceedings of the VLDB Endowment 15, 8 (2022), 1697–1711.
[181] John Paparrizos, Chunwei Liu, Bruno Barbarioli, Johnny Hwang, Ikraduya Edian, Aaron J Elmore, Michael J Franklin, and Sanjay Krishnan. 2021.
VergeDB: A Database for IoT Analytics on Edge Devices… In CIDR.
[182] John Paparrizos, Chunwei Liu, Aaron J Elmore, and Michael J Franklin. 2020. Debunking four long-standing misconceptions of time-series distance
measures. In Proceedings of the 2020 ACM SIGMOD international conference on management of data. 1887–1905.
[183] John Paparrizos, Chunwei Liu, Aaron J. Elmore, and Michael J. Franklin. 2023. Querying Time-Series Data: A Comprehensive Comparison of
Distance Measures. IEEE Data Eng. Bull. 46, 3 (2023), 69–88. http://sites.computer.org/debull/A23sept/p69.pdf
[184] John Paparrizos and Sai Prasanna Teja Reddy. 2023. Odyssey: An engine enabling the time-series clustering journey. Proceedings of the VLDB
Endowment 16, 12 (2023), 4066–4069.
[185] John Paparrizos, Ryen W White, and Eric Horvitz. 2016. Detecting devastating diseases in search logs. In Proceedings of the 22nd ACM SIGKDD
International Conference on Knowledge Discovery and Data Mining. 559–568.
[186] John Paparrizos, Ryen W White, and Eric Horvitz. 2016. Screening for pancreatic adenocarcinoma using signals from web search logs: Feasibility
study and results. Journal of oncology practice 12, 8 (2016), 737–744.
[187] John Paparrizos, Kaize Wu, Aaron Elmore, Christos Faloutsos, and Michael J Franklin. 2023. Accelerating similarity search for elastic measures: A
study and new generalization of lower bounding distances. Proceedings of the VLDB Endowment 16, 8 (2023), 2019–2032.
[188] Nicos G Pavlidis, Vassilis P Plagianakos, Dimitris K Tasoulis, and Michael N Vrahatis. 2006. Financial forecasting through unsupervised clustering
and neural networks. Operational Research 6, 2 (2006), 103–127.
[189] Karl Pearson. 1901. LIII. On lines and planes of closest fit to systems of points in space. The London, Edinburgh, and Dublin philosophical magazine
and journal of science 2, 11 (1901), 559–572.
[190] François Petitjean, Alain Ketterlin, and Pierre Gançarski. 2011. A global averaging method for dynamic time warping, with applications to
clustering. Pattern recognition 44, 3 (2011), 678–693.
[191] Domenico Piccolo. 1990. A distance measure for classifying ARIMA models. Journal of time series analysis 11, 2 (1990), 153–164.
[192] Shai Policker and Amir B Geva. 2000. Nonstationary time series analysis by temporal clustering. IEEE Transactions on Systems, Man, and Cybernetics,
Part B (Cybernetics) 30, 2 (2000), 339–343.
[193] Jiang Qian, Marisa Dolled-Filhart, Jimmy Lin, Haiyuan Yu, and Mark Gerstein. 2001. Beyond synexpression relationships: local clustering of
time-shifted and inverted gene expression profiles identifies new, biologically relevant interactions. Journal of molecular biology 314, 5 (2001),
1053–1066.
[194] Marco Ramoni, Paola Sebastiani, and Paul Cohen. 2000. Multivariate clustering by dynamics. In AAAI/IAAI. 633–638.
[195] William M Rand. 1971. Objective criteria for the evaluation of clustering methods. Journal of the American Statistical association 66, 336 (1971),
846–850.
[196] Teemu Räsänen and Mikko Kolehmainen. 2009. Feature-based clustering for electricity use time series data. In Adaptive and Natural Computing
Algorithms: 9th International Conference, ICANNGA 2009, Kuopio, Finland, April 23-25, 2009, Revised Selected Papers 9. Springer, 401–412.
[197] Chotirat Ratanamahatana, Eamonn Keogh, Anthony J Bagnall, and Stefano Lonardi. 2005. A novel bit level time series representation with
implication of similarity search and clustering. In Pacific-Asia conference on knowledge discovery and data mining. Springer, 771–777.
[198] Chotirat Ann Ratanamahatana and Eamonn Keogh. 2005. Three myths about dynamic time warping data mining. In Proceedings of the 2005 SIAM
international conference on data mining. SIAM, 506–510.
[199] LKPJ Rdusseeun and P Kaufman. 1987. Clustering by means of medoids. In Proceedings of the statistical data analysis based on the L1 norm conference,
neuchatel, switzerland, Vol. 31.
[200] Lei Ren, Yongchang Wei, Jin Cui, and Yi Du. 2017. A sliding window-based multi-stage clustering and probabilistic forecasting approach for large
multivariate time series data. Journal of Statistical Computation and Simulation 87, 13 (2017), 2494–2508.
[201] Pedro Pereira Rodrigues, Joao Gama, and Joao Pedroso. 2008. Hierarchical clustering of time-series data streams. IEEE transactions on knowledge
and data engineering 20, 5 (2008), 615–627.
[202] Alex Rodriguez and Alessandro Laio. 2014. Clustering by fast search and find of density peaks. science 344, 6191 (2014), 1492–1496.
[203] Frank Rosenblatt. 1958. The perceptron: a probabilistic model for information storage and organization in the brain. Psychological review 65, 6
(1958), 386.
[204] Peter J Rousseeuw. 1987. Silhouettes: a graphical aid to the interpretation and validation of cluster analysis. Journal of computational and applied
mathematics 20 (1987), 53–65.
[205] David E Rumelhart, Geoffrey E Hinton, and Ronald J Williams. 1986. Learning representations by back-propagating errors. nature 323, 6088 (1986),
533–536.
[206] Nicholas Ruta, Naoko Sawada, Katy McKeough, Michael Behrisch, and Johanna Beyer. 2019. Sax navigator: Time series exploration through
hierarchical clustering. In 2019 IEEE Visualization Conference (VIS). IEEE, 236–240.
[207] Hiroaki Sakoe and Seibi Chiba. 1978. Dynamic programming algorithm optimization for spoken word recognition. IEEE transactions on acoustics,
speech, and signal processing 26, 1 (1978), 43–49.
[208] Patrick Schäfer and Mikael Högqvist. 2012. SFA: a symbolic fourier approximation and index for similarity search in high dimensional datasets.
In Proceedings of the 15th International Conference on Extending Database Technology (Berlin, Germany) (EDBT ’12). Association for Computing
Machinery, New York, NY, USA, 516–527. https://doi.org/10.1145/2247596.2247656
[209] Onur Seref, Ya-Ju Fan, and Wanpracha Art Chaovalitwongse. 2014. Mathematical programming formulations and algorithms for discrete k-median
clustering of time-series data. INFORMS Journal on Computing 26, 1 (2014), 160–172.
[210] Vivek Sharma, Makarand Tapaswi, M Saquib Sarfraz, and Rainer Stiefelhagen. 2020. Clustering based contrastive learning for improving face
representations. In 2020 15th IEEE International Conference on Automatic Face and Gesture Recognition (FG 2020). IEEE, 109–116.
[211] CT Shaw and GP King. 1992. Using cluster analysis to classify time series. Physica D: Nonlinear Phenomena 58, 1-4 (1992), 288–298.
[212] Jin Shieh and Eamonn Keogh. 2009. iSAX: disk-aware mining and indexing of massive time series datasets. Data Mining and Knowledge Discovery
19, 1 (2009), 24–57.
[213] Robert H Shumway. 2003. Time-frequency clustering and discriminant analysis. Statistics & probability letters 63, 3 (2003), 307–314.
[214] Karen Simonyan and Andrew Zisserman. 2014. Very deep convolutional networks for large-scale image recognition. arXiv preprint arXiv:1409.1556
(2014).
[215] Alexandra Stefan, Vassilis Athitsos, and Gautam Das. 2012. The move-split-merge metric for time series. IEEE transactions on Knowledge and Data
Engineering 25, 6 (2012), 1425–1438.
[216] Michael Steinbach, Pang-Ning Tan, Vipin Kumar, Steven Klooster, and Christopher Potter. 2003. Discovery of Climate Indices Using Clustering. In
Proceedings of the Ninth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (Washington, D.C.) (KDD ’03). Association
for Computing Machinery, New York, NY, USA, 446–455. https://doi.org/10.1145/956750.956801
[217] Adrian Stetco, Xiao-jun Zeng, and John Keane. 2013. Fuzzy cluster analysis of financial time series and their volatility assessment. In 2013 IEEE
International Conference on Systems, Man, and Cybernetics. IEEE, 91–96.
[218] Alexander Strehl and Joydeep Ghosh. 2002. Cluster ensembles—a knowledge reuse framework for combining multiple partitions. Journal of
machine learning research 3, Dec (2002), 583–617.
[219] Colin Studholme, Derek LG Hill, and David J Hawkes. 1999. An overlap invariant entropy measure of 3D medical image alignment. Pattern
recognition 32, 1 (1999), 71–86.
[220] Numanul Subhani, Luis Rueda, Alioune Ngom, and Conrad J Burden. 2010. Multiple gene expression profile alignment for microarray time-series
data clustering. Bioinformatics 26, 18 (2010), 2281–2288.
[221] Mukund Subramaniyan, Anders Skoogh, Azam Sheikh Muhammad, Jon Bokrantz, Björn Johansson, and Christoph Roser. 2020. A generic
hierarchical clustering approach for detecting bottlenecks in manufacturing. Journal of Manufacturing Systems 55 (2020), 143–158.
[222] Emmanouil Sylligardos, Paul Boniol, John Paparrizos, Panos Trahanias, and Themis Palpanas. 2023. Choose wisely: An extensive evaluation of
model selection for anomaly detection in time series. Proceedings of the VLDB Endowment 16, 11 (2023), 3418–3432.
[223] Xue Wang Liang Sun Rong Jin Tian Zhou, Peisong Niu. 2023. One Fits All: Power General Time Series Analysis by Pretrained LM. In NeurIPS.
[224] Donato Tiano, Angela Bonifati, and Raymond Ng. 2021. FeatTS: Feature-based time series clustering. In Proceedings of the 2021 International
Conference on Management of Data. 2784–2788.
[225] Donato Tiano, Angela Bonifati, and Raymond Ng. 2021. Feature-driven time series clustering. In 24th International Conference on Extending
Database Technology, EDBT 2021.
[226] Sana Tonekaboni, Danny Eytan, and Anna Goldenberg. 2021. Unsupervised Representation Learning for Time Series with Temporal Neighborhood
Coding. In International Conference on Learning Representations. https://openreview.net/forum?id=8qDwejCuCN
[227] Dat Tran and Michael Wagner. 2002. Fuzzy C-Means Clustering-Based Speaker Verification. In Advances in Soft Computing — AFSS 2002, Nikhil R.
Pal and Michio Sugeno (Eds.). Springer Berlin Heidelberg, Berlin, Heidelberg, 318–324.
[228] Daniel J Trosten, Andreas S Strauman, Michael Kampffmeyer, and Robert Jenssen. 2019. Recurrent deep divergence-based clustering for simultaneous
feature learning and clustering of variable length time series. In ICASSP 2019-2019 IEEE International Conference on Acoustics, Speech and Signal
Processing (ICASSP). IEEE, 3257–3261.
[229] Liudmila Ulanova, Nurjahan Begum, and Eamonn Keogh. 2015. Scalable clustering of time series with u-shapelets. In Proceedings of the 2015 SIAM
international conference on data mining. SIAM, 900–908.
[230] Jarke J Van Wijk and Edward R Van Selow. 1999. Cluster and calendar based visualization of time series data. In Proceedings 1999 IEEE Symposium
on Information Visualization (InfoVis’ 99). IEEE, 4–9.
[231] Ashish Vaswani, Noam Shazeer, Niki Parmar, Jakob Uszkoreit, Llion Jones, Aidan N Gomez, Łukasz Kaiser, and Illia Polosukhin. 2017. Attention is
all you need. Advances in neural information processing systems 30 (2017).
[232] Petar Veličković, Guillem Cucurull, Arantxa Casanova, Adriana Romero, Pietro Liò, and Yoshua Bengio. 2018. Graph Attention Networks. In
International Conference on Learning Representations. https://openreview.net/forum?id=rJXMpikCZ
[233] Michail Vlachos, George Kollios, and Dimitrios Gunopulos. 2002. Discovering similar multidimensional trajectories. In Proceedings 18th international
conference on data engineering. IEEE, 673–684.
[234] Xiaozhe Wang, Kate Smith, and Rob Hyndman. 2006. Characteristic-based clustering for time series data. Data mining and knowledge Discovery 13
(2006), 335–364.
[235] XiaozheWang, Kate A Smith, and Rob J Hyndman. 2005. Dimension reduction for clustering time series using global characteristics. In International
Conference on Computational Science. Springer, 792–795.
[236] Xiaozhe Wang, Anthony Wirth, and Liang Wang. 2007. Structure-based statistical features and multivariate time series clustering. In Seventh IEEE
international conference on data mining (ICDM 2007). IEEE, 351–360.
[237] Joe H Ward Jr. 1963. Hierarchical grouping to optimize an objective function. Journal of the American statistical association 58, 301 (1963), 236–244.
[238] J Wilpon and L Rabiner. 1985. A modified K-means clustering algorithm for use in isolated work recognition. IEEE Transactions on Acoustics,
Speech, and Signal Processing 33, 3 (1985), 587–594.
[239] Axel Wismüller, Oliver Lange, Dominik R Dersch, Gerda L Leinsinger, Klaus Hahn, Benno Pütz, and Dorothee Auer. 2002. Cluster analysis of
biomedical image time-series. International Journal of Computer Vision 46, 2 (2002), 103–128.
[240] Jun Wu, Zelin Zhang, Rui Tong, Yuan Zhou, Zhengfa Hu, and Kaituo Liu. 2023. Imaging feature-based clustering of financial time series. Plos one
18, 7 (2023), e0288836.
[241] Zhirong Wu, Yuanjun Xiong, Stella X Yu, and Dahua Lin. 2018. Unsupervised feature learning via non-parametric instance discrimination. In
Proceedings of the IEEE conference on computer vision and pattern recognition. 3733–3742.
[242] Andreas Wunsch, Tanja Liesch, and Stefan Broda. 2022. Feature-based groundwater hydrograph clustering using unsupervised self-organizing
map-ensembles. Water Resources Management 36, 1 (2022), 39–54.
[243] Zhiwen Xiao, Huanlai Xing, Bowen Zhao, Rong Qu, Shouxi Luo, Penglin Dai, Ke Li, and Zonghai Zhu. 2023. Deep Contrastive Representation
Learning with Self-Distillation. IEEE Transactions on Emerging Topics in Computational Intelligence (2023).
[244] Junyuan Xie, Ross Girshick, and Ali Farhadi. 2016. Unsupervised deep embedding for clustering analysis. In International conference on machine
learning. PMLR, 478–487.
[245] Yimin Xiong and Dit-Yan Yeung. 2002. Mixtures of ARMA models for model-based time series clustering. In 2002 IEEE International Conference on
Data Mining, 2002. Proceedings. IEEE, 717–720.
[246] Chenxiao Xu, Hao Huang, and Shinjae Yoo. 2021. A deep neural network for multivariate time series clustering with result interpretation. In 2021
International Joint Conference on Neural Networks (IJCNN). IEEE, 1–8.
[247] Ziwei Xu, Xudong Shen, YongkangWong, and Mohan S Kankanhalli. 2021. Unsupervised motion representation learning with capsule autoencoders.
Advances in Neural Information Processing Systems 34 (2021), 3205–3217.
[248] Bo Yang, Xiao Fu, Nicholas D Sidiropoulos, and Mingyi Hong. 2017. Towards k-means-friendly spaces: Simultaneous deep learning and clustering.
In international conference on machine learning. PMLR, 3861–3870.
[249] Fan Yang, Muqiao Yang, Xiang Li, Yuxuan Wu, Zhiyuan Zhao, Bhiksha Raj, and Rita Singh. 2024. A closer look at reinforcement learning-based
automatic speech recognition. Computer Speech & Language 87 (2024), 101641. https://doi.org/10.1016/j.csl.2024.101641
[250] Jaewon Yang and Jure Leskovec. 2011. Patterns of temporal variation in online media. In Proceedings of the fourth ACM international conference on
Web search and data mining. 177–186.
[251] Ling Yang and Shenda Hong. 2022. Unsupervised time-series representation learning with iterative bilinear temporal-spectral fusion. In International
Conference on Machine Learning. PMLR, 25038–25054.
[252] Xinyu Yang, Zhenguo Zhang, and Rongyi Cui. 2022. Timeclr: A self-supervised contrastive learning framework for univariate time series
representation. Knowledge-Based Systems 245 (2022), 108606.
[253] Lexiang Ye and Eamonn Keogh. 2009. Time series shapelets: a new primitive for data mining. In Proceedings of the 15th ACM SIGKDD international
conference on Knowledge discovery and data mining. 947–956.
[254] Chin-Chia Michael Yeh, Yan Zhu, Liudmila Ulanova, Nurjahan Begum, Yifei Ding, Hoang Anh Dau, Diego Furtado Silva, Abdullah Mueen, and
Eamonn Keogh. 2016. Matrix Profile I: All Pairs Similarity Joins for Time Series: A Unifying View That Includes Motifs, Discords and Shapelets. In
2016 IEEE 16th International Conference on Data Mining (ICDM). 1317–1322. https://doi.org/10.1109/ICDM.2016.0179
[255] Byoung-Kee Yi and Christos Faloutsos. 2000. Fast time sequence indexing for arbitrary Lp norms. (2000).
[256] Zhihan Yue, Yujing Wang, Juanyong Duan, Tianmeng Yang, Congrui Huang, Yunhai Tong, and Bixiong Xu. 2022. Ts2vec: Towards universal
representation of time series. In Proceedings of the AAAI Conference on Artificial Intelligence, Vol. 36. 8980–8987.
[257] Jesin Zakaria, Abdullah Mueen, and Eamonn Keogh. 2012. Clustering time series using unsupervised-shapelets. In 2012 IEEE 12th International
Conference on Data Mining. IEEE, 785–794.
[258] George Zerveas, Srideepika Jayaraman, Dhaval Patel, Anuradha Bhamidipaty, and Carsten Eickhoff. 2021. A transformer-based framework
for multivariate time series representation learning. In Proceedings of the 27th ACM SIGKDD conference on knowledge discovery & data mining.
2114–2124.
[259] Hongjun Zhang, Jing Wang, Qinfeng Xiao, Jiaoxue Deng, and Youfang Lin. 2021. Sleeppriorcl: Contrastive representation learning with prior
knowledge-based positive mining and adaptive temperature for sleep staging. arXiv preprint arXiv:2110.09966 (2021).
[260] Nan Zhang and Shiliang Sun. 2022. Multiview unsupervised shapelet learning for multivariate time series clustering. IEEE Transactions on Pattern
Analysis and Machine Intelligence 45, 4 (2022), 4981–4996.
[261] Qin Zhang, Jia Wu, Hong Yang, Yingjie Tian, and Chengqi Zhang. 2016. Unsupervised feature learning from time series… In IJCAI. New York, USA,
2322–2328.
[262] Qin Zhang, JiaWu, Peng Zhang, Guodong Long, and Chengqi Zhang. 2018. Salient subsequence learning for time series clustering. IEEE transactions
on pattern analysis and machine intelligence 41, 9 (2018), 2193–2207.
[263] Xiaohang Zhang, Jiaqi Liu, Yu Du, and Tingjie Lv. 2011. A novel clustering method on time series data. Expert Systems with Applications 38, 9
(2011), 11891–11900.
[264] Xiang Zhang, Ziyuan Zhao, Theodoros Tsiligkaridis, and Marinka Zitnik. 2022. Self-supervised contrastive pre-training for time series via
time-frequency consistency. Advances in Neural Information Processing Systems 35 (2022), 3988–4003.
[265] Zheng Zhang, Xuzhi Lai, Min Wu, Luefeng Chen, Chengda Lu, and Sheng Du. 2021. Fault diagnosis based on feature clustering of time series data
for loss and kick of drilling process. Journal of Process Control 102 (2021), 24–33.
[266] Ying Zhong, Dong Huang, and Chang-Dong Wang. 2023. Deep Temporal Contrastive Clustering. Neural Processing Letters (2023), 1–17.
[267] Yan Zhu, Zachary Zimmerman, Nader Shakibay Senobari, Chin-Chia Michael Yeh, Gareth Funning, Abdullah Mueen, Philip Brisk, and Eamonn
Keogh. 2016. Matrix Profile II: Exploiting a Novel Algorithm and GPUs to Break the One Hundred Million Barrier for Time Series Motifs and Joins.
In 2016 IEEE 16th International Conference on Data Mining (ICDM). 739–748. https://doi.org/10.1109/ICDM.2016.0085
[268] Robert J Zupko, Tran Dang Nguyen, J Claude S Ngabonziza, Michee Kabera, Haojun Li, Thu Nguyen-Anh Tran, Kien Trung Tran, Aline Uwimana,
and Maciej F Boni. 2023. Modeling policy interventions for slowing the spread of artemisinin-resistant pfkelch R561H mutations in Rwanda.
Nature Medicine 29, 11 (2023), 2775–2784.