【每日文献阅读】Hierarchical Classification of Dynamically Varying PRI modulation patterns

Hierarchical classification of dynamically varying radar pulse repetition interval modulation patterns

Jukka-Pekka Kauppi a,∗, Kalle Martikainen b, Ulla Ruotsalainen a
a 坦佩雷理工大学，信号处理系，邮政信箱553，FI-33101 坦佩雷，芬兰
b 帕特里亚航空有限公司，瑙拉卡图3号，FI-33100 坦佩雷，芬兰

摘要

无源信号截获接收机的核心目标是实现对未知雷达信号的自动分类。当前，由于雷达波形日益复杂，亟需为这类设备开发智能分类算法。尤其是多功能雷达（Multifunction Radars, MFRs），其能通过发射复杂、动态变化的调度波形同时执行多项任务，成为自动模式分类系统面临的重大挑战。为助力现代截获接收机识别复杂雷达辐射信号，本文提出一种新方法，用于识别MFRs发射的动态变化脉冲重复间隔（Pulse Repetition Interval, PRI）调制模式。该方法采用鲁棒的特征提取与分类器设计技术，以应对不可预测的实际信号环境。本文对接收的脉冲序列进行分层分类，通过滑动窗口实现对子模式的无歧义检测。通过对静态和动态变化PRI调制模式的大量仿真，验证了该技术的准确性、鲁棒性与可靠性。

1. 引言

现代无源信号截获接收机是高度复杂的数字传感器，旨在宽射频（Radio Frequency, RF）频谱范围内截获并分类周围的雷达辐射信号。需要对未知雷达信号进行分类的潜在应用场景包括：用于防范非法移民、武器与毒品走私、非法捕鱼及海盗活动的海上屏障行动（Menhinick, 2005）；在军事危机期间，分类则可用于在存在威胁辐射时向防御系统发出警报（Schleher, 1999）。

图1展示了无源信号截获接收机中雷达辐射源分类的主要流程。信号截获后，入射雷达脉冲首先在脉冲参数编码器中进行参数化处理，生成描述单个雷达脉冲参数的脉冲描述字（Pulse Descriptor Words, PDWs），这些参数包括射频（RF）、脉冲幅度（Pulse Amplitude, PA）、脉冲宽度（Pulse Width, PW）、到达时间（Time of Arrival, TOA）、到达方向（Direction of Arrival, DOA）、脉冲上升/下降时间以及脉内调制类型。

在复杂信号环境中，可能存在多个同时工作的辐射源，因此接收的脉冲序列通常是来自多个辐射源的交错脉冲序列。交错脉冲需在解交错器中进行分选，将来自同一辐射源的PDWs聚类到一起（Anderson, Gately, Penz, & Collins, 1990; Ata’a & Abdullah, 2007; Granger, Rubin, Grossberg, & Lavoie, 2001; Liu, Lee, Li, Luo, & Wong, 2005; Mardia, 1989）。随后，单个辐射源的PDW序列将进入脉冲间调制编码器处理，该编码器负责识别并估计序列中脉冲间参数变化模式的参数。其中，通过序列中连续TOA值的差值识别信号的PRI调制模式，可获取尤为重要的信息；此外，还可识别RF与PW捷变模式及天线波束模式，以进一步了解辐射源类型及其功能用途。

脉冲间调制编码器生成名为辐射源描述字（Emitter Descriptor Words, EDWs）的文件，该文件尽可能准确地描述雷达信号中最相关的脉内和脉冲间参数。最终，EDWs将与主动收集的威胁库进行匹配，以识别辐射源；若无法识别，则仅基于提取的EDW参数评估其功能用途与威胁等级。

为确保在多辐射源复杂信号环境中可靠工作，现代截获接收机必须能够鲁棒且可靠地处理未知、失真及模糊的测量数据（Roe, Cussons, & Feltham, 1990）。近年来，随着多功能雷达（MFRs，又称电扫描雷达）的出现，分类问题更具挑战性。这类雷达通过发射高度多样且不可预测的扫描波形，同时执行搜索、多目标跟踪等多项任务，且其RF、PW与PRI均具备捷变特性（Arasaratnam, Haykin, Kirubarajan, & Dilkes, 2006; Visnevski, Krishnamurthy, Wang, & Haykin, 2007; Wirth, 2001）。

在许多情况下（从无源信号截获的角度而言），雷达的辐射特性无法预先获知，因此，要揭示雷达的意图，唯一途径便是自动分析其波形特征。其中，雷达脉冲间调制（如PRI、RF及PW调制）的识别已成为截获接收机信号处理的核心问题，因为它能提供关于雷达功能用途的宝贵信息。由于现有许多方法仅适用于具有静态辐射特性的传统雷达，现代截获接收机亟需开发新的脉冲间识别算法。

为此，本文提出一种可用于识别MFRs发射的复杂PRI调制模式的新方法。该方法的核心是一组不变特征集，该特征集能够在特征空间中区分所有基本PRI调制类型（参见Kauppi与Martikainen于2007年的研究）。本文提出的分类方案利用这些特征，以分层方式识别PRI调制模式：首先基于粗分类别信息，通过滑动窗口在整个序列中检测PRI调制子结构；随后，利用二级分类器对提取的子模式进行更精确的分类。这种分层分类方案可确保无歧义地捕获整个序列中的不同PRI调制子结构。

在该框架下，本文实现了一个示例性分类器，可自动处理失真或其他意外序列。在实际应用中，避免此类序列的误分类至关重要——若将用于敌对活动的辐射信号误分类为无害信号，后果可能极为严重；此时，更优的选择是向防御平台发出未知辐射信号的警报。

本文其余部分结构如下：第2节首先描述基本PRI调制类别（2.1节），然后回顾并讨论现有PRI调制识别技术的局限性（2.2节）；第3节介绍PRI调制识别的新方法，包括特征提取（3.1节）和分层分类（3.2节）两个主要部分；第4节通过大量蒙特卡洛仿真信号环境，给出示例性分类器设计；第5节提供多种仿真的可视化与定量识别结果；最后，第6节对研究进行总结。

2. PRI调制识别

2.1 PRI调制类别

PRI调制的一般描述如下：

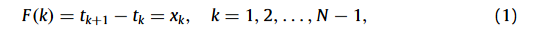
其中，$t_k$ 为第$k$个脉冲的TOA，$x_k$ 表示第$k$个脉冲间隔（又称TOA差值，dTOA），$N$ 为序列中的总脉冲数。根据发射序列的不同，函数$F$（用于描述PRI调制规律）可具有不同形式。本文中，“脉冲序列（pulse train）”与“PRI序列（PRI sequence）”可互换使用，均指来自单个辐射源的脉冲序列（尽管序列中可能存在来自其他辐射源的虚假脉冲）。

根据雷达的任务与智能程度，一个脉冲序列可能包含多个连续的、具有独特特征的PRI调制子模式。下文将依据Wiley（2006, 2007）的研究，描述最常见的PRI调制类别。

基本PRI调制类型可分为六类，分别为：恒定（Constant）PRI、参差（Stagger）PRI、抖动（Jittered）PRI、滑动（Sliding）PRI、驻留与切换（Dwell & Switch）PRI以及周期性（Periodic）PRI。尽管详细讨论超出本文范围，但需注意：根据参数设置的不同，每类PRI调制均可与一种或多种雷达功能相关联。

• 若脉冲间隔变化量小于平均PRI的1%，则可归类为恒定PRI，因为这种变化几乎无法实现任何有用功能；
• 若雷达以周期性方式在脉冲间切换脉冲间隔，则产生的变化称为参差PRI。“参差位置数”指构成一个周期的脉冲间隔总数，一个周期内可能多次出现相同的脉冲间隔值。例如，两个相等的短脉冲间隔后接一个长脉冲间隔的周期性重复序列，对应“3个位置的参差PRI”（即周期长度为3），但该序列中仅包含2个不同的脉冲间隔值。现代雷达的参差位置数可从2个到64个不等；
• 抖动PRI指脉冲间隔的有意随机变化，变化量最高可达平均PRI的30%（Wiley, 2006）。这种变化通常服从高斯分布、均匀分布、非均匀分布或离散分布。对于离散抖动PRI，预计最多可能存在64个不同的脉冲间隔值；
• 滑动PRI指连续脉冲间隔的单调增加或减少。滑动通常具有周期性：当脉冲间隔达到一个极值时，会快速切换至另一个极值。在某些应用中，可能出现极大的变化量，但也可能存在变化量受限的情况；
• 驻留与切换PRI由两个或多个极稳定的恒定PRI突发段（burst）组成，这些突发段可能周期性重复，也可能不重复。不同雷达及雷达模式下，单个突发段中的脉冲间隔数差异显著；一个周期内的突发段数可从2个到16个，甚至更多；
• 周期性PRI指脉冲间隔呈正弦或三角波形式变化。在导弹制导应用中，预计变化量较小（小于平均PRI的5%），频率约为50 Hz；但若周期性PRI用于其他用途，则可能出现更大的变化量。

传统雷达通常发射属于上述某一类别的长脉冲序列，而现代MFR可发射由多个连续调制模式组成的序列，这类模式被称为“调度PRI（Scheduled PRIs）”（Wiley, 2006）。由于MFR会以自适应方式调度不同任务（如搜索、捕获、多目标跟踪、导弹制导）（Wirth, 2001），因此不同调制模式的精确数量与长度无法预先获知。例如，发射模式的数量会根据跟踪目标的数量及其位置而变化。然而，在一个波束驻留时间内，发射的PRI序列通常与上述六种基本PRI调制类型中的某一种相同或极为相似。

2.2 现有技术

现有PRI调制类型识别技术大致可分为两类：一类利用PRI直方图（PRI histogram），另一类利用脉冲间隔的序列信息来区分不同PRI调制类型。

PRI直方图分析是支持传统人工操作PRI调制类型识别的常用技术。但遗憾的是，直方图不适用于周期性、滑动等PRI调制类型的自动识别——对于这些调制类型，直方图的形状会随可用脉冲数量、直方图组距选择以及截获脉冲序列中缺陷（如丢失、虚假脉冲）的数量而变化。不过，直方图在识别涉及独特脉冲间隔值的PRI调制类型（如参差PRI、恒定PRI）时更具实用价值。

Mardia（1989）提出的基于直方图的技术主要用于脉冲解交错，但也可用于识别恒定PRI与参差PRI。该技术基于“累积差分（Cumulative Difference, CDIF）直方图”中的峰值检测，CDIF直方图用于表示序列中选定脉冲对的出现频率。若CDIF直方图中的任意峰值超过预设检测阈值，则从交错脉冲序列中提取与该峰值对应的脉冲序列。

Milojević与Popović（1992）对上述原始技术进行了改进，将CDIF直方图替换为更简单、计算效率更高的“序列差分（Sequential Difference, SDIF）直方图”。一阶SDIF直方图（又称PRI直方图）可近似反映序列中dTOA的分布；二阶SDIF直方图考虑序列中每个脉冲与间隔一个脉冲的后续脉冲之间的时间间隔，以此类推。因此，d阶SDIF直方图表示以下时间间隔的出现频率：

图2展示了理想2位置参差PRI序列的前两阶SDIF直方图。在一阶SDIF直方图（图2(a)）中，没有任何峰值超过指数检测阈值；而二阶时间间隔是恒定的，因此在二阶直方图（图2(b)）中会出现一个强峰值。该峰值被称为“稳定和（stable sum）”——只要有足够的脉冲，任何周期性脉冲模式都会存在稳定和。

一般而言，若脉冲序列的周期包含d个脉冲间隔，且无缺陷，则在d阶SDIF直方图中可观察到指示稳定和的单个峰值。但若脉冲序列存在失真，直方图中的虚假峰值会使稳定和的检测难度显著增加。

上述峰值检测技术的主要局限性在于：其设计初衷主要是实现脉冲解交错及区分恒定PRI与参差PRI，并未考虑更复杂的PRI调制类型；另一缺点是对阈值选择的依赖性极强，而阈值需根据脉冲序列中的缺陷数量来确定。

统计类技术的一个显著不足是会丢失脉冲序列的所有序列信息，导致不同调制类型之间存在歧义。例如，参差PRI、驻留与切换PRI、离散抖动PRI的PRI直方图均以“独特峰值”为特征；高阶SDIF直方图也可能存在歧义——因为稳定和不仅存在于参差PRI中，还存在于其他所有周期性调制模式中。

为克服直方图相关问题，研究人员提出了一些基于脉冲间隔序列信息的方法。Ryoo、Song与Kim（2007）提出了一种基于自相关的特征提取技术，可识别四种PRI调制类型（滑动、抖动、驻留与切换、周期性）。但由于该技术提取的特征对实际环境中的缺陷（如丢失、虚假脉冲）敏感，因此在特征提取前必须对丢失脉冲进行补偿，并去除虚假脉冲。然而，在实际应用中，预处理的使用可能不可行——因为该方法对PRI调制参数的设置做出了限制性假设。

Noone（1999）利用dTOA的差分信息构建了N维特征向量。该技术的主要缺点是：所提特征对常见参数变化（如规则PRI调制模式的长度、相位变化）不具有不变性。为实现更灵活的识别，Rong、Jin与Zhang（2006）提出将特征向量的维度从N降至2。该技术无需固定N的值，且在复杂识别环境中比Noone（1999）的方法具有更高的识别精度，但在区分能力方面，其特征仍存在较大局限性。

3. 方法

本节首先介绍用于区分六种PRI调制类型的鲁棒特征集（3.1节），然后提出一种可用于识别这些PRI调制模式序列组合的分层分类概念（3.2节）。

3.1 特征提取

特征提取在PRI调制识别中起着关键作用——精心选择的特征可显著简化实际分类任务，提高识别的准确性与可靠性。由于对脉冲序列进行预处理可能导致调制模式的独特特征丢失，因此需寻找无需预处理即可有效工作的特征。

理想特征应满足以下要求：

1. 容忍脉冲序列中的大量缺陷（包括丢失脉冲、虚假脉冲及连续TOA测量误差）；
2. 对参数设置变化（包括模式间的幅度、偏差、相位变化）具有鲁棒性；
3. 不受脉冲序列间调制周期长度变化的影响。

此前研究（Kauppi & Martikainen, 2007）已表明，五个特征可在特征空间中区分六种PRI调制类型。这些特征描述了PRI序列的以下属性：（1）单一直方图峰值；（2）稳定和；（3）脉冲间隔变化；（4）单向脉冲间隔变化；（5）脉冲间隔的局部极值。下文将对这些特征进行回顾。

3.1.1 基于直方图的特征

前两个特征从直方图中提取。在实际应用中，由于脉冲序列存在TOA不确定性，恒定脉冲间隔序列对应的直方图峰值可能分布在两个或多个直方图组距内。为确保直方图峰值的鲁棒检测，本文采用“算法1：直方图峰值稳定算法”计算直方图。该算法的核心步骤为：首先将脉冲间隔按升序排序，然后逐个分配到当前组距中，直至某个脉冲间隔无法适配当前组距；基于该脉冲间隔的值创建新组距，并继续直方图的构建过程。

算法1：直方图峰值稳定算法

本文将该算法作为特征提取的一部分，用于构建PRI直方图及多阶SDIF直方图。

第一个特征是PRI直方图中两个最高峰值的比值，表达式如下：
$$f_1=\frac{n^{max-1}}{n^{max}}$$
其中，$n^{max}$ 表示最高峰值的频数，$n^{max-1}$ 表示第二高峰值的频数。显然，较小的特征值表明不存在有意调制（即恒定PRI）。

第二个特征从高阶SDIF直方图中提取，描述稳定和的相对强度。由于稳定和可突出周期性，且并非随机序列的特征，因此该特征特别适用于区分抖动PRI与参差PRI。d阶SDIF直方图中稳定和的相对强度定义为：
$$u_d=\frac{n_d^{max}-{\mu }_d}{{\sigma }_d}$$
其中，$n_d^{max}$ 为d阶SDIF直方图中的最高峰值频数，${\mu }_d$ 为直方图的均值，${\sigma }_d$ 为直方图的标准差。

由于参差PRI的位置数通常未知，因此需计算多个d值对应的$u_d$，并将最大值作为最终特征值：
$$f_2=\underset{d=1,2,...,D_{max}}{\max }{u}_d$$
其中，$D_{max}$ 根据参差PRI的最大预期位置数确定。相对抖动容忍度${\epsilon }_r$ 是需预先确定的用户参数。

3.1.2 基于序列信息的特征

后三个特征描述脉冲序列的序列信息。首先，根据Noone（1999）的方法，由式（1）（注：原文式（1）为PRI调制的一般描述，核心是TOA与dTOA的关系）计算脉冲序列的二阶TOA差值（$d^2$TOA）向量：
$$z_k=x_{k+1}-x_k,k=1,2,...,N-2$$
需注意该式与构建SDIF直方图所用式（2）（注：原文式（2）为d阶SDIF直方图的时间间隔定义）的区别。

通过以下变换仅保留方向信息（Noone, 1999）：
$$s_k=sg{n}_{\epsilon }(z_k),k=1,2,...,N-2$$
其中，$z$ 为序列中所有$d^2$TOA构成的向量，$sg{n}_{\epsilon }(\cdot )$ 为带容忍度的符号函数，定义为：
$$sg{n}_{\epsilon }\left(z_n\right)=\{\begin{array}{ll}-1,& 当z_n<-\epsilon \\ 0,& 当\left|z_n\right|\le \epsilon \\ 1,& 当z_n>\epsilon \end{array}$$
此处，$\epsilon$ 为抖动容忍度，用于区分脉冲间隔的无意微小变化与有意调制。

• 特征3：描述连续脉冲间隔变化的相对数量，表达式为：
  $$f_3=\sum _{k=1}^{N-2}\left|s_k\right|/(N-2)$$
  其中，$s_k$ 为式（5）（注：即上述$s_k=sg{n}_{\epsilon }(z_k)$）定义的向量的第$k$个元素。该特征可有效区分稳定PRI序列与非稳定PRI序列。

• 特征4：描述脉冲序列中单向脉冲间隔变化的相对数量，表达式为：
  $$f_4=\frac{1}{N-2}\max \left\{\sum _{k=1}^{N-2}I(s_k=1),\sum _{k=1}^{N-2}I(s_k=-1)\right\}$$
  其中，$I(\cdot )$ 为指示函数（满足条件时取1，否则取0）。该特征特别适用于区分滑动PRI与其他调制类型。

• 特征5：描述脉冲间隔变化方向的切换频率，表达式为：
  $$f_5=\frac{1}{N-3}\sum _{k=1}^{N-3}\left|sgn(r_k)\right|$$
  其中，$sgn(\cdot )$ 为标准符号函数，$r_k=s_{k+1}-s_k$（$k=1,2,...,N-3$）。该特征尤其适用于区分抖动PRI与周期性PRI。

3.2 分层分类

为识别调度PRI的不同PRI调制子模式，本文提出：不采用现有研究中对整个脉冲序列进行识别的方式，而是通过滑动窗口对脉冲序列进行时间维度上的分析。然而，对短片段进行特征提取与分类存在一个问题——最优窗口大小取决于PRI调制参数的设置，而不同脉冲序列的参数设置可能存在任意差异。

图3展示了直接识别脉冲序列片段时出现的问题：窗口$M_2$适用于对顶部所示PRI序列进行分段，因为滑动窗口时，每个窗口帧均可捕获驻留与切换PRI的相关特征；但该窗口不适用于底部序列的识别——多个窗口帧会同时包含驻留与切换PRI和参差PRI的特征。尽管较小的窗口$M_1$在此情况下适用，但反过来又不适用于顶部序列的分段——因为窗口帧包含的信息不足，可能导致驻留与切换PRI被误判为恒定PRI。

上述例子表明，直接识别序列片段在实际应用中并不可靠（固定窗口大小易导致歧义，尤其是在恒定PRI与驻留与切换PRI、参差PRI与抖动PRI、滑动PRI与周期性PRI之间）。为降低识别结果对窗口大小选择的依赖性，本文建议在实际分类前先对子网模式进行粗检测。

子模式检测通过滑动窗口执行，但由于仅利用粗分类信息，检测结果对窗口大小选择不敏感。以图3为例，若将驻留与切换PRI和恒定PRI视为单个超级类别，则窗口$M_1$对两个序列均为有效窗口。

3.2.1 分层分类框架

图4(a)展示了用于识别调度PRI调制模式的完整分类方案。在第一阶段，子模式检测器通过滑动窗口从整个脉冲序列中寻找并提取具有静态特性的子模式（窗口大小$M$由每个窗口帧捕获的dTOA数量决定）。子模式检测器根据以下粗分类信息对每个片段进行分类：

1. 稳定PRI（Stable PRIs）：连续脉冲间隔值无变化或仅有偶发变化；
2. 定向PRI（Directional PRIs）：脉冲间隔呈递增和/或递减排序；
3. 非定向PRI（Non-directional PRIs）：窗口帧内的脉冲间变化不稳定，且不遵循递增/递减排序。

将这些模式的对应类别标签记为${\theta }_i$（i∈{1,2,3}i \in \{1,2,3\}i∈{1,2,3}）。若子模式检测器发现连续窗口帧的类别标签${\theta }_k$与${\theta }_l$满足$k\ne l$，则表明PRI序列的特性已发生变化。此时，子模式检测器从整个序列中提取子模式，并将其传递至最终分类阶段。

随后，相应的组件分类器为该子模式分配实际类别标签${\omega }_i$（i∈{1,2,...,6}i \in \{1,2,...,6\}i∈{1,2,...,6}），或在必要时将其标记为“不确定”并丢弃。由于提取后已知超级类别标签，最终阶段的识别问题可简化为三个二分类问题——这源于PRI调制固有的分层结构（见图4(b)）：

• 稳定PRI的子类别：恒定PRI、驻留与切换PRI；
• 定向PRI的子类别：周期性PRI、滑动PRI；
• 非定向PRI的子类别：抖动PRI、参差PRI。

4. 仿真与实现

本节首先给出示例性分类器设计，随后介绍仿真示例。选择符合实际的仿真模型是分类器设计中极为重要的环节——只有基于实际仿真，才能确保分类器在真实世界不可预测的信号环境中实现可靠、准确的识别。确定仿真模型后，组件分类器的选择具有多种可能性。本文选择多层感知器（Multi-Layer Perceptron, MLP）作为子模式检测器，并选择三个独立的核密度估计器（Kernel Density Estimators, KDEs）作为最终分类器。选择这些分类器的主要原因如下：

1. 它们可提供类别归属的后验概率估计，有助于监控分类的不确定性；
2. 实现效率高（对于KDE，一维情况下尤为如此）；
3. 无需任何分布假设；
4. 若后续修改仿真模型，易于重新实现。

4.1 合成数据生成

通过大量蒙特卡洛仿真，生成描述复杂信号环境的特征分布。仿真的参数范围如表1所示。为每个PRI调制类别生成等量的脉冲序列，脉冲序列参数从表1所示范围中均匀抽取。共生成$n=36000$个脉冲序列，即每个类别包含6000个样本。生成脉冲序列后，根据式（3）、式（4）（取$D_{max}=64$）及式（7）-（9）（注：即特征1-5的表达式）执行特征提取。

表1 辅助分类的建议模型

参数类别	具体参数与范围
平均PRI的偏差	抖动PRI（均匀、高斯${}^a$）：5%–50%；周期性PRI：4%–50%；滑动PRI${}^b$：1:20
位置数/突发段数	参差PRI${}^c$：2–64；驻留与切换PRI${}^d$：2–16；离散抖动PRI：32–64
单个突发段的脉冲数	驻留与切换PRI${}^e$：8–100
周期数	周期性PRI、滑动PRI：1–20；参差PRI：5–160
缺陷参数	丢失脉冲：0%–15%；虚假脉冲：0%–10%；TOA不确定性：$0\le 2\sigma \le \epsilon$

${}^a$：高斯模型的偏差由3σ范围确定；${}^b$：偏差定义为最小PRI与最大PRI的比值；${}^c$：对于p个位置的参差PRI，不同脉冲间隔值的数量范围为$\max [2,p-2]$至p；${}^d$：同时建模周期性与非周期性模式；${}^e$：对于给定脉冲序列，最长突发段与最短突发段的长度比上限为3:1。

在提出的模型中，不同PRI调制类型的调制参数允许存在极大变异性。抖动PRI根据三种不同分布（均匀、高斯、离散）建模。需指出的是，尽管参数允许存在显著变异性，但由于特征的不变性，蒙特卡洛参数范围的具体选择并非关键问题。例如，无需对不同脉冲重复频率的脉冲序列进行建模——因为特征对dTOA的幅度具有不变性。

脉冲序列中的缺陷数量取决于多种因素，如信噪比（SNR）、雷达定时电路、接收机测量精度以及脉冲检测器、脉冲参数提取器、脉冲解交错器的设计。本文假设在正常工作条件下，序列中可能丢失15%的脉冲，或存在10%的随机虚假脉冲；同时，假设正常工作条件下存在轻微的TOA测量不确定性（包括无意的PRI变化），因此向序列的连续脉冲间隔中添加零均值、独立的高斯噪声（将噪声标准差的上限设为$\epsilon /2$，即约5%的原始稳定脉冲间隔值会超过容忍度$\epsilon$）。

作为特殊情况，恒定PRI允许的无意变化量大于其他PRI调制类型（Wiley, 2006）。为确保特征分布被充分采样，对36000个脉冲序列的缺陷建模如下：

• 随机选择9000个序列，通过增加TOA测量不确定性引入缺陷；
• 随机选择另外9000个序列，通过随机丢弃脉冲引入缺陷；
• 随机选择另外9000个序列，通过混入虚假脉冲引入缺陷；
• 剩余9000个序列无任何缺陷。

4.2 组件分类器设计

4.2.1 子模式检测器

训练一个三层MLP，用于子模式检测器中的粗分类。选择MLP的原因之一是：经过适当训练后，MLP可有效利用仿真数据中包含的信息——其决策边界几乎可以是任意复杂的（这与简单的树分类器不同，树分类器的决策边界只能垂直于特征轴）。

MLP的另一大优势是能够估计分类结果的不确定性（Richard & Lippmann, 1991）——该特性至关重要，因为它可检测训练数据中未明确包含的意外脉冲序列。此外，MLP对分类结果的评估速度极快，这是所提应用的关键要求。

MLP的网络设计与分类器训练通过Matlab的神经网络工具箱完成。从36000个仿真数据样本中随机选取18000个样本用于网络训练。训练过程中，采用标准反向传播算法计算均方误差（Mean Squared Error, MSE）代价函数对网络权重与偏置的导数；采用拟牛顿BFGS（布罗伊登-弗莱彻-戈德法布-香农）更新算法最小化MSE准则——该算法在仿真中可实现快速且稳定的收敛。网络采用批量模式训练，目标向量为二进制向量；训练在500个epoch后停止，因为此后总训练误差无明显变化。

• 输出层大小：3（与超级类别的总数相等）；
• 输入层大小：3（基于对仿真数据的详细分析，发现粗分类PRI调制模式需用到特征$f_1$、$f_3$、$f_5$，参见5.1节）；
• 隐藏层大小：8（通过以下模型选择流程确定）。

模型选择流程如下：首先，针对具有不同隐藏节点数的多个训练候选MLP，利用独立测试数据集（由仿真数据中未用于训练的18000个样本组成）评估其性能，并采用以下模型选择准则：
$$\max \left|z_{ij}-t_{ij}\right|\le 0.1(i=1,2,3)$$
其中，$z_{ij}$ 为测试数据集中第$j$个特征向量在第$i$个输出节点的激活值，$t_{ij}$ 为对应的理想目标输出。更具体地，若将第$j$个测试样本记为$f^{(j)}$，则当$f^{(j)}\in {\theta }_i$时，对应的目标输出$t_{ij}=1$；否则$t_{ij}=0$。

重要的是，该准则同时考虑了MLP的输出是否能近似类别标签与类别归属的后验概率——只有当每个输出节点的激活值与理想0-1目标概率的差异小于10%时，准则才成立。

按复杂度递增的顺序（从3个隐藏节点的MLP开始），依据上述准则评估每个候选MLP。最终选择满足“99%以上测试样本符合准则”的最简单MLP作为分类器。8个隐藏节点的MLP可满足该要求（99.1%的测试样本符合式（10））。选择99%作为阈值是因为：超过该阈值后，即使增加网络复杂度，结果也无稳定提升。

测试集的分类精度极高，表明所选MLP未出现过拟合问题。原因在于：三维特征分布的采样极为充分（训练与测试均使用18000个样本）。

训练并确定MLP后，采用滑动窗口执行实际的子模式检测与分类。为提高检测器对序列片段中突发异常变化的鲁棒性，仅当连续至少5个窗口帧均检测到子模式时，才确认子模式的检测结果。

经验性地将MLP的拒绝阈值设为0.95：若某一片段对应的MLP最大输出激活值低于该阈值，则将该片段标记为“不确定”，不进行后续分类。

4.2.2 最终分类器

对特征分布的分析表明，单个特征（$f_1$、$f_2$或$f_4$）即可满足子模式最终分类的需求（参见5.1节）。因此，构建三个一维组件分类器，用于最终识别阶段的二分类。

为实现分类结果的不确定性估计，在三种情况下均采用帕森法（Parzen, 1962，又称核密度估计）估计训练分布的概率密度函数（PDF）。在实际应用中，基于帕森估计的分类规则可通过两种方式确定：一是视觉检查，二是应用贝叶斯准则（将样本分配给后验概率最高的类别）（Duda, Hart, & Stork, 2001）。后一种方式可设置概率阈值，用于监控识别不确定性并丢弃意外模式。

由于仿真中分类器1与分类器3的特征分布无重叠（参见5.1节），因此基于视觉检查确定其分类规则：

• 分类器1（稳定PRI子分类）：若$f_1\le 0.25$，则判定为恒定PRI；若$f_1\ge 0.50$，则判定为驻留与切换PRI；否则拒绝该模式。
• 分类器3（定向PRI子分类）：若$f_4\le 0.25$，则判定为滑动PRI；若$f_4\ge 0.50$，则判定为周期性PRI；否则拒绝该模式。

分类器2（非定向PRI子分类）采用贝叶斯准则计算类别归属（两类的先验概率均设为0.50），并将拒绝阈值设为0.95——即需至少95%的置信度才能为模式分配类别标签。

4.3 测试序列

为验证所提方法的分类精度与拒绝能力，构建包含10个不同PRI调制子模式的复杂测试序列。表2展示了序列中每个子模式的类别及关键参数。通过改变子模式中的脉冲数量，观察方法对不同长度模式的处理能力；通过纳入参数差异极大的PRI调制模式，检验分类器对调制参数大幅变化的鲁棒性。

例如，生成了具有短周期（3个位置）和长周期（32个位置）的参差PRI；驻留与切换PRI模式也存在显著差异——一个包含多个短PRI突发段，另一个仅包含三个长突发段；周期性PRI包含不同幅度的长期与短期变化；抖动PRI则分别基于离散分布与高斯分布建模。

表2 测试序列描述

子模式编号与类别	具体参数
1：参差PRI	脉冲数：120；位置数：3
2：滑动PRI	脉冲数：180；周期数：5；偏差（最小:最大）：1:2
3：驻留与切换PRI	类型：周期性；脉冲数：150；一个周期内的突发段数：8；单个突发段脉冲数：8–15
4：抖动PRI	分布：离散；脉冲数：220；离散PRI数量：64
5：恒定PRI	脉冲数：140
6：参差PRI	脉冲数：320；位置数：32
7：周期性PRI	脉冲数：330；平均PRI偏差：5%；一个周期内的脉冲数：110；周期数：3
8：驻留与切换PRI	类型：非周期性；脉冲数：300；突发段数：3；单个突发段脉冲数：85、90或125
9：抖动PRI	分布：高斯；脉冲数：240；标准差：3%
10：周期性PRI	脉冲数：170；平均PRI偏差：25%；一个周期内的脉冲数：10；周期数：17

5. 结果

5.1 特征集分离能力

对特征分布的视觉检查是评估所提方法性能的重要环节——因为具有区分能力的特征集是实现可靠实际识别的基本要求。

图5展示了整个仿真数据（$n=36000$）在三维特征空间（$f_1,f_3,f_5$）中的特征分布，这些特征用于MLP的子模式检测。显然，利用特征$f_1$、$f_3$、$f_5$可很好地分离三个超级类别：

• 利用特征$f_5$（局部极值）可区分定向PRI与非定向PRI；
• 利用特征$f_3$（脉冲间隔变化）可完全分离稳定PRI与定向PRI；
• 在（$f_3,f_5$）平面中，稳定PRI与非定向PRI类别存在部分重叠——原因是仿真模型允许恒定PRI的无意变化量大于其他调制类型；但通过增加特征$f_1$（单一直方图峰值），可消除这种重叠。

最终组件分类器所用仿真数据的帕森估计如图6所示（采用高斯核，平滑参数$h=2/n^{1/2}$）：

• 图6(a)：恒定PRI与驻留与切换PRI的分布通过特征$f_1$可实现极佳分离；
• 图6(c)：周期性PRI与滑动PRI的分布通过特征$f_4$可实现极佳分离；
• 图6(b)：参差PRI与抖动PRI的分布存在部分重叠——这种重叠是任何特征都无法完全避免的，因为当序列中的随机缺陷较多时，参差PRI会逐渐接近离散抖动PRI。

图7展示了采用Rong等人（2006）提出的特征在二维特征空间中绘制的相同数据。此时，大多数分布存在严重重叠，表明这两个特征不足以实现可靠的实际分类。尽管“频率特征”可较好地将滑动PRI与其他PRI调制类别区分开，但本文采用的特征$f_4$（单向脉冲间隔变化）无需将序列转换至频域，即可实现类似的分离效果。所提“形状特征”本质上与本文的$f_5$（脉冲间隔变化方向切换频率）相似。

5.2 测试序列分类结果

5.2.1 窗口大小的影响

图8展示了在不同窗口大小下，测试序列中正确分类的子模式数量（正确检测）与虚假/误分类子模式数量（错误检测），并分别考察了理想情况与缺陷情况（启用/禁用拒绝选项）。

在缺陷情况下，首先从原始序列中随机移除7.5%的TOA，然后插入7.5%的随机TOA。

• 图8(a)：理想测试序列，禁用拒绝选项。在较宽的窗口大小范围（$30\le M\le 160$）内，成功检测到所有10个真实子模式；但由于未启用拒绝选项，使用大窗口时会出现不必要的子模式。进一步分析表明，这些虚假模式位于不同子模式的边界区域。
• 图8(b)：理想测试序列，启用拒绝选项。在多个窗口大小（$30\le M\le 130$）下，检测到所有真实模式，且所有错误检测均被有效消除。
• 图8©、(d)：缺陷测试序列的结果。即使在该情况下，启用拒绝选项后（图8(d)），所有错误检测仍被有效消除；但由于分类结果存在不确定性，部分真实子模式被检测为“未知”。

综上，所提分层分类器结合拒绝选项后，测试序列的识别效果非常理想：结果对窗口大小选择的依赖性不强，且错误检测可被有效消除。

5.2.2 序列级结果

图9展示了窗口大小$M=60$时，理想测试序列的序列级分类结果（窗口大小根据图8的结果选择）：

• 图9(a)：测试序列的dTOA；
• 图9(b)：每个片段的MLP输出激活值（水平虚线表示拒绝阈值0.95）。显然，MLP以极高的置信度近似了10个子模式的粗分类归属；类别归属之间的过渡非常陡峭，表明每个子模式的定位精度很高（提取点用彩色圆圈标记）；
• 图9(c)：提取子模式的最终分类结果及对应目标类别。所有10个模式均被正确分类，且定位精度高。

图10展示了缺陷测试序列的对应结果：

• 图10(a)：缺陷测试序列的dTOA（双间隔对应随机丢失的脉冲，分裂间隔对应随机插入的脉冲）；
• 图10(b)：子模式检测结果。MLP能以高置信度识别稳定PRI与非定向PRI；尽管定向PRI（子模式#2、#7、#10）的不确定性较高，但仍可被检测到；该方法对某一输出节点激活值的临时丢失（参见子模式#7的MLP输出）及极短的激活峰值（参见子模式#2与#3之间的输出）具有鲁棒性；
• 图10©：最终分类结果。10个模式中有9个被正确识别，32位置参差PRI（子模式#6）被检测为“未知”。该拒绝结果并不意外——即使通过人工检查，也难以区分该序列与离散抖动PRI序列。

5.2.3 对缺陷的鲁棒性

为更系统地测试分类器对实际缺陷的鲁棒性，表3总结了窗口大小$M=50$时，测试序列在不同缺陷条件（丢失脉冲、虚假脉冲、高斯噪声）下的识别结果。表中报告了找到的子模式总数（正确检测）、误分类或虚假模式总数（错误检测），以及被误分类或检测为“未知”的子模式编号。

• 丢失脉冲：当原始序列中5%的脉冲丢失时，所有真实模式均被识别；当丢失10%–15%的脉冲时，仅子模式#6（32位置参差PRI）被报告为“未知”；当丢失20%–25%的脉冲时，额外有两个子模式被拒绝。值得注意的是，即使丢失25%的脉冲，也未观察到错误检测——该测试条件比仿真模型假设的（最多丢失15%脉冲）更具挑战性。
• 虚假脉冲：结果与丢失脉冲的情况类似。仅当存在20%的随机插入脉冲时，出现一次误分类（滑动PRI模式#2被误分为周期性PRI）。
• 高斯噪声：向测试序列中插入高斯噪声后，序列中出现大量无意PRI变化（变化量为固定抖动容忍度$\epsilon$的2–5倍），尤其对序列的稳定部分造成失真。尽管分类器训练时未考虑此类条件，但结果中未出现误分类或额外子模式。

表3 实际缺陷条件下的分类结果（$M=50$）

缺陷类型	缺陷程度	正确检测	错误检测	误分类模式	未知模式
丢失脉冲（%）	5	10	0	–	–
	10	9	0	–	#6
	15	9	0	–	#6
	20	7	0	–	#1、#2、#6
	25	7	0	–	#1、#3、#6
虚假脉冲（%）	5	9	0	–	#6
	10	9	0	–	#6
	20	8	1	#2	#6
抖动噪声（×ε）	2	8	0	–	#3、#5
	3	4	0	–	#3、#4、#5、#6、#7、#8
	4	4	0	–	#3、#4、#5、#6、#7、#8
	5	4	0	–	#3、#4、#5、#6、#7、#8

5.3 讨论

综上，所提分类器在模拟实际信号环境的多种挑战性识别条件下，均能持续获得理想结果：只要不同调制模式的独特特征得以保留，识别结果就具有很高的准确性；当存在意外或模糊模式时，可始终避免误分类；此外，结果对窗口大小选择的依赖性不强。

尽管仿真中测试了多种识别条件，但仍有至少两种重要情况需进一步研究：

1. 需结合不同窗口大小，深入分析极短子模式（如脉冲间隔数少于50个）的识别问题；
2. 需研究子模式顺序任意变化情况下的子模式检测问题。例如，参差PRI与抖动PRI的序列组合在实际中难以提取——因为这两种模式属于同一粗分类别；但通过在最终分类前增加专用检测器，或许可实现此类组合的提取与检测。

6. 结论

本文提出一种用于雷达PRI调制模式自动识别的新方法，以支持无源雷达截获接收机中的实际雷达辐射源分类。研究重点是解决MFRs发射的调度（动态变化）PRI调制模式的识别问题，但所提思路也适用于其他类型脉冲间调制模式（如静态与调度PW、RF捷变模式）的识别。

该方法采用两阶段分层分类方案：首先基于脉冲间隔排序的粗分类信息，从整个脉冲序列中检测并提取具有一致特性的不同子模式；随后，对提取的子模式进行更详细的分类。即使允许调制模式存在显著参数变化与大量缺陷，所提方法仍具有较高的准确性；重要的是，该方法可自动检测不确定性较高的脉冲序列。

未来工作包括：基于PRI调制识别结果估计调制参数、实现该方法的实时化、设计更结构化的分层分类器。

致谢

作者感谢Richard G. Wiley博士对仿真真实性提出的宝贵意见与建议。本研究部分得到芬兰科学院（项目编号213462，2006–2011年芬兰卓越研究中心计划）资助，部分得到坦佩雷信息科学与工程研究生院（TISE）资助。

图片列表：