决策树

决策树（decision tree）：是一种基本的分类与回归方法，此处主要讨论分类的决策树。

决策树通常有三个步骤：特征选择、决策树的生成、决策树的修剪。

决策树学习的目标：根据给定的训练数据集构建一个决策树模型，使它能够对实例进行正确的分类。

决策树学习的本质：从训练集中归纳出一组分类规则，或者说是由训练数据集估计条件概率模型。

决策树学习的损失函数：正则化的极大似然函数

一 特征选择

信息熵：

当熵中的概率由数据估计(特别是最大似然估计)得到时，所对应的熵称为经验熵(empirical entropy)。什么叫由数据估计？比如有10个数据，一共有两个类别，A类和B类。其中有7个数据属于A类，则该A类的概率即为十分之七。其中有3个数据属于B类，则该B类的概率即为十分之三。浅显的解释就是，这概率是我们根据数据数出来的。

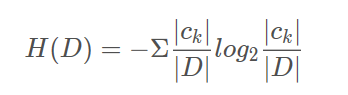
条件信息熵：

信息增益表示得知特征X的信息而使得类Y的信息不确定性减少的程度。

条件熵H(Y∣X)表示在已知随机变量X的条件下随机变量Y的不确定性，随机变量X给定的条件下随机变量Y的条件熵，定义X给定条件下Y的条件概率分布的熵对X的数学期望：

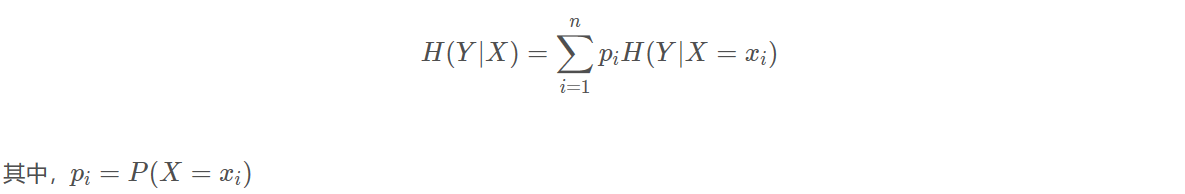
信息增益：

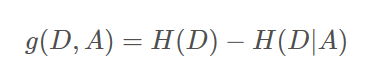
信息增益比：

信息增益作为划分训练数据集的特征，存在偏向于选择取值较多的特征的问题。使用信息增益比可以对这一问题进行校正。

基尼指数：

基尼指数Gini(D)表示集合D不确定性，基尼指数Gini(D，A=a)表示集合D经A=a分割后的不确定性(类似于熵)，基尼指数越小，样本的不确定性越小。

二 决策树生成

生成算法	划分标准
ID3	信息增益
C4.5	信息增益率
CART	基尼指数

ID3：

C4.5：