写在前面
如果你会SAMSAMSAM,相信回文自动机不会难懂。
如果你不会,你可以参考我的上一篇文章。
至少回文自动机是治愈系的吧。
作用
回文自动机,也叫回文树,简称PAMPAMPAM实际上它既不是自动机也不是树
处理回文串的有力工具。可完全代替ManacherManacherManacher,就是会多个字符集。
算法流程
首先一个结论:往一个串末尾加入一个字符,最多会增加一个没出现过的回文串。
证明:
假设出现了两个之前没有出现的,它们都是当前串的后缀。
根据对称性,把短的关于长的的中心作对称,得到一个相同的回文串,说明已经出现过了。
矛盾,所以最多出现一个。
这么说,对于字符串SSS,本质不同的回文串最多有∣S∣|S|∣S∣个。
于是可以每个状态表示一个本质相同的回文串。用lenilen_ileni表示状态iii表示的回文串的长度。
考虑到回文串两边一样的,定义转移ccc表示当前串左右各加上一个ccc
因为分奇回文和偶回文,所以定义两个初始节点0,10,10,1,其中len[0]=0,len[1]=−1len[0]=0,len[1]=-1len[0]=0,len[1]=−1(让len[1]=−1len[1]=-1len[1]=−1可以说是这个算法最妙的地方)
000表示偶回文,111表示奇回文。−1-1−1可以看做添加时吞掉一个字符。

类比ACACAC自动机,定义fail[i]fail[i]fail[i]为这个回文串的最长非自己的回文后缀(以下简称回文真后缀)。
强行让fail[0]=fail[1]=1fail[0]=fail[1]=1fail[0]=fail[1]=1
实际上有个隐含条件:1的所有转移都到0
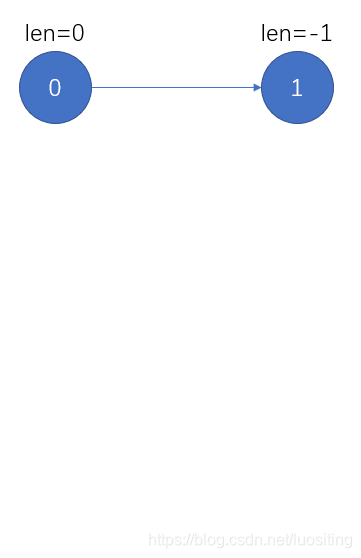
接下来同样考虑增量。
当我们插入S[i]S[i]S[i]时,现在我们知道S[i−1]S[i-1]S[i−1]的所有回文后缀,要求S[i]S[i]S[i]的回文后缀。
我们可以从前一个点跳failfailfail,如果到某个点ppp刚好可以前后接上S[i]S[i]S[i],即S[i−len[p]−1]=S[i]S[i-len[p]-1]=S[i]S[i−len[p]−1]=S[i],说明有一个ppp到当前点的转移。
如果已经有转移了,说明这个回文串出现过,直接退出。
接下来维护failfailfail。我们发现最长回文真后缀和它本身具有相同的性质。
在之前的基础上继续跳就可以了。如果跳到某个ppp有S[i]S[i]S[i]的转移,说明ch[p][S[i]]ch[p][S[i]]ch[p][S[i]]是个回文后缀,连过去就可以了。
栗子:AABAAABAAABA
插入AAA
此时len[1]=−1len[1]=-1len[1]=−1的优势就体现出来了,因为刚好是S[i]=S[i]S[i]=S[i]S[i]=S[i]
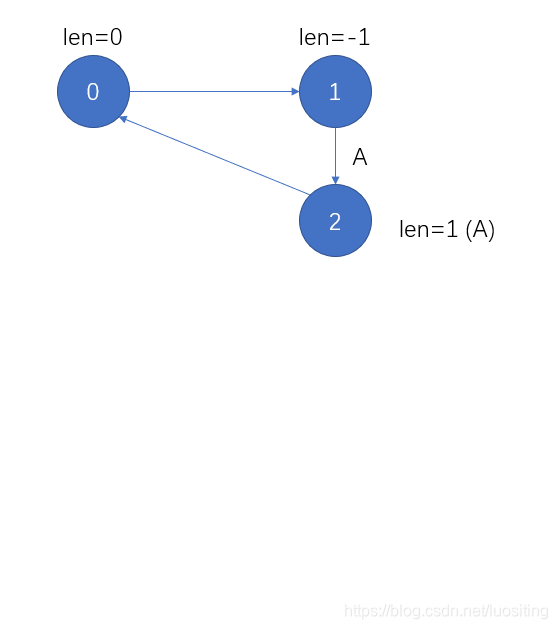
插入AAA,依次跳到0,10,10,1
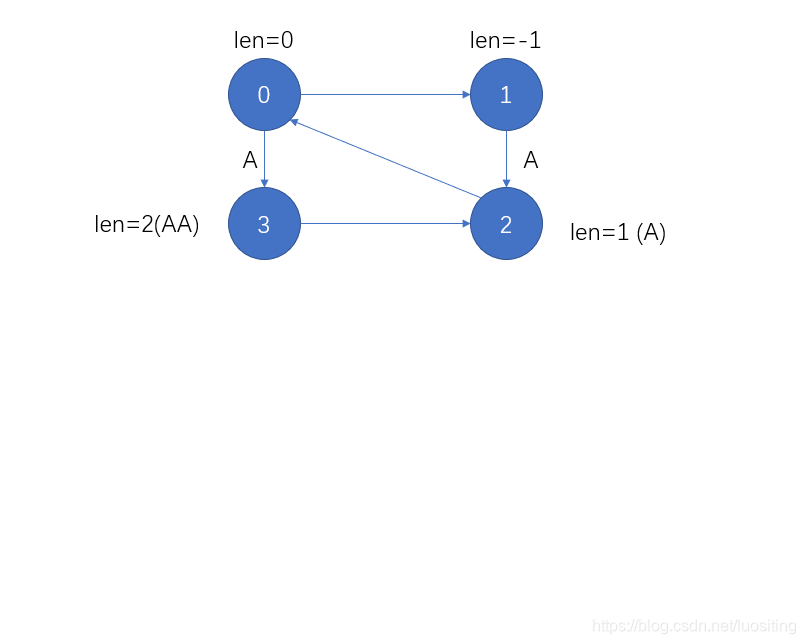
插入BBB
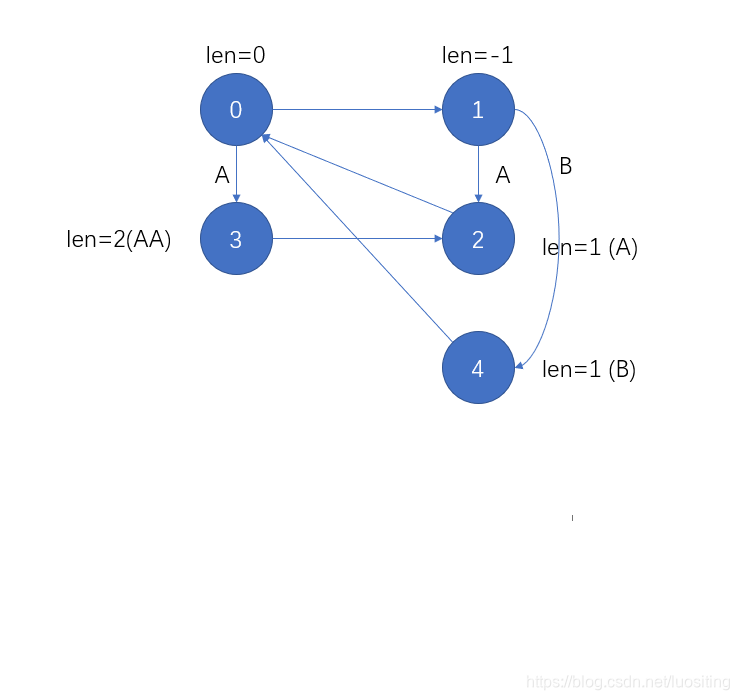 插入AAA
插入AAA
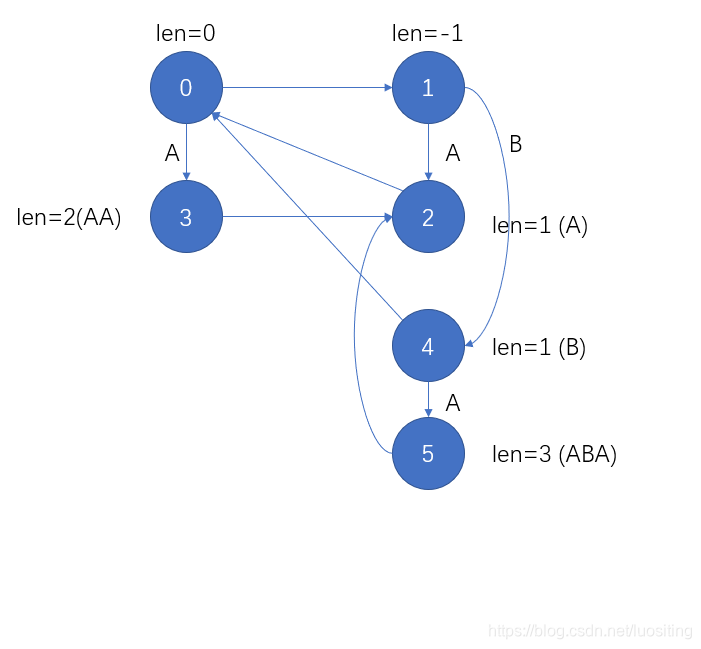
实现
第一步插入的时候由于一些玄学问题,ppp的failfailfail可能接到自己身上
解决策略是先把fail算出来,再接到之前的节点后面
剩下的就很容易了
代码有点古怪,仅供参考
char s[MAXN];
int n;
int ch[MAXN][26],fail[MAXN];
int len[MAXN];
int las=1,tot=1;
void init()
{
len[1]=-1;
fail[0]=fail[1]=1;
}
void insert(int i)
{
int p=las;
while (s[i-len[p]-1]!=s[i]) p=fail[p];
if (ch[p][s[i]-'a']) return (void)(las=ch[p][s[i]-'a']);
int q=fail[p];
while (s[i-len[q]-1]!=s[i]) q=fail[q];
las=++tot;
fail[las]=ch[q][s[i]-'a'];
len[ch[p][s[i]-'a']=las]=len[p]+2;
}
运用
①每个点结尾的回文个数
即failfailfail树的深度
②本质不同的回文个数
就是状态数
好像只有这些……
想到再补吧




 本文深入解析回文自动机(PAMPAMPAM),一种处理回文串的强大工具,可替代Manacher算法,适用于多种字符集。文章阐述了算法流程、核心结论及其实现细节,包括如何通过增量方式构建回文自动机,以及如何利用失败指针优化查找过程。
本文深入解析回文自动机(PAMPAMPAM),一种处理回文串的强大工具,可替代Manacher算法,适用于多种字符集。文章阐述了算法流程、核心结论及其实现细节,包括如何通过增量方式构建回文自动机,以及如何利用失败指针优化查找过程。
















 168万+
168万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








