几个冷门字符串算法的学习笔记（最小表示法，exKMP，Lyndon Word）

所有下标均从1开始

最小表示法

给定一个串，求字典序最小的循环同构。

我们把串复制一遍接在后面，然后求出$[1,N]$开始的长为$N$的子串中最小的

先设$i=1,j=2$

然后暴力找出$i$和$j$往后匹配的第一个不同的位置，记为$i+k$和$j+k$

如果$S_{i+k}<S_{j+k}$,说明$i$比$j$优，所以$j$不是最优解；然后发现$i+1$比$j+1$优，所以$j+1$不是最优解……这样可以让$j$直接跳到$j+k+1$。

$S_{i+k}>S_{j+k}$同理

如果$i=j$，随便让一个$+1$即可

两个指针都不能超过$N$，一个超过之后另一个就是答案

因为所有位置都会被遍历，而最优解一定不会被丢掉，所以正确性可以保证。

复杂度显然是$O(N)$

模板题

#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
char s[10005];
int main()
{
	int T;
	scanf("%d",&T);
	while (T--)
	{
		scanf("%s",s);
		int n=strlen(s);
		int i=0,j=1;
		while (i<n&&j<n)
			for (int k=0;;k++)
			{
				if (s[(i+k)%n]!=s[(j+k)%n])
				{
					if (s[(i+k)%n]>s[(j+k)%n])
						i+=k+1;
					else 
						j+=k+1;
					if (i==j) j++;
					break;
				}
				if (k==n) goto end;
			}
		end:
		printf("%d\n",min(i,j)+1);
	}
	return 0;
}

(远古代码，和上面讲的略有不同，仅供参考)

扩展KMP

官方名称应该叫Z算法，不知道为啥传到国内就变成扩展KMP了

但实际上思想和manacher很像所以应该叫扩展马拉车

解决的问题是给两个串$S,T$,求 $T$的每个后缀和$S$ 的最长公共前缀

先把$S$接在$T$后面，中间加个#之类的东西 把这个串记为$A$

然后设$p_i$表示$A$的从$i$开始的后缀和$T$（也可以是$A$）的最长公共前缀

并且设公共前缀扩展到的最右位置为$mx$,取到这个最大值的$i$为$x$

然后$i$从$2$开始遍历（因为$p_1$没有意义还会把算法搞砸）

如果$i<mx$

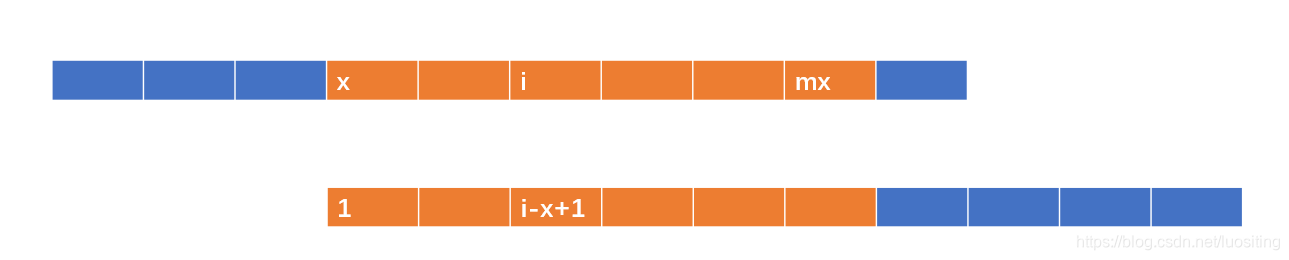
因为上下橙色位置相同，所以$p_i=p_{i-x+1}$，当然要和$mx-i+1$取$\min$

如果$i\ge mx$，不管

然后暴力扩展，更新$mx$,没了

复杂度显然$O(|S|+|T|)$

模板题

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cctype>
#define MAXN 200005
using namespace std;
char s[MAXN],t[MAXN];
int p[MAXN];
int main()
{
	scanf("%s%s",t+1,s+1);
	int m=strlen(s+1);
	strcat(s+1,"#");
	strcat(s+1,t+1);
	int n=strlen(s+1);
	for (int i=2,x=0,mx=0;i<=n;i++)
	{
		p[i]=i<=mx? min(p[i-x+1],mx-i+1):0;
		while (s[i+p[i]]==s[p[i]+1]) ++p[i];
		if (i+p[i]-1>mx) x=i,mx=i+p[i]-1;
	}
	for (int i=1;i<=n;i++)
		if (s[i]=='#') puts("");
		else printf("%d ",i>1? p[i]:m);
	return 0;
}

Lyndon Word

定义：一个串是Lyndon Word（以下简称LW），当且仅当它本身是自己字典序最小的后缀

下文字符串的比较均为字典序，+为字符串拼接

性质1 两个LW $u,v$,如果$u<v$,那么$u+v$是LW

对于$v$的后缀，它比$v$大，所以一定不是最小的；

对于$v$,因为$u<v$,所以$u+v<v$

对于$(u的后缀)+v$,因为$u<(u的后缀)$,所以$u+v<(u的后缀)+v$

所以$u+v$是最小的

所以LW可以递归定义：

1. 单个字符是LW
2. 多个字典序递增的LW顺次拼接后是LW

性质2 一个LW将最后一个字符变大后仍是LW

只有最后一个只包含一个字符的后缀变大，前面大小关系不变

性质3 任意字符串$S$存在且仅存在一种分解方式$S=s_1+s_2+...+s_n$,使得所有$s_i$均为LW且单调不增

证明是不可能的，这辈子都是不可能的

把性质3中的分解称为Lyndon分解

接下来要讲的就是线性求Lyndon分解的Duval算法

首先三个指针$i,j,k$，表示$i$以前的分解已经固定,现在处理第$k$个字符,$j$一会儿说

即$[1,i)$为$s_1+s_2+...+s_n$,其中$s_i$为LW且单调不增

$[i,k)$为$t+t+...+t+t_1$,其中$t$是LW，$t_1$是$t$的可空前缀

也就是一个LW不断循环，最后一个循环节可以不完整。注意这不一定是$[i,k)$的Lyndon分解，因为$t_1$不一定是LW

别问为啥，问就是归纳法

现在把$S_k$加在后面，如果要继续循环，应该加的是$S_{k-循环节长度}$，我们把这个$k$应该跟的位置记为$j$

如果$S_j=S_k$，说明循环正常，继续往后

如果$S_j<S_k$，根据性质1，最后一个不完整的循环节$t_1$加上$S_k$是个LW并且比前面的$t$都大，不断向前合并发现整段都是LW。所以将$[i,k]$一长串合并成新的$t$，即令$j=i$

如果$S_j>S_k$ 不管$t_1$和$S_k$大小关系，反正后面怎么加怎么都会小于$t$,所以没$t$啥事了，把所有$t$固定下来，$t_1$作为新的循环节。然后$t_1$这个地方，我们之前以为它会进入循环，然而它没有，这里面漏了一些信息，所以需要从$t_1$的开头重新分解

模板题

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cctype>
#define MAXN (1<<20)+5
using namespace std;
char s[MAXN];
int main()
{
	scanf("%s",s+1);
	int n=strlen(s+1);
	for (int i=1;i<=n;)
	{
		int j=i,k=i+1;
		while (s[j]<=s[k])
		{
			if (s[j]==s[k]) ++j;
			else j=i;
			++k;
		}
		while (i<=j)
		{
			printf("%d ",i+k-j-1);
			i+=k-j;
		}
	}
	return 0;
}

我 华 灯 宴 呢