【模糊数学】模糊逻辑，隶属度，模糊逻辑应用，模糊推理过程

【update】下一篇博客我将会讲如何用这篇博客的模糊推理过程构建一个图像边缘检测的模糊推理系统~~~

链接：https://blog.youkuaiyun.com/luolan9611/article/details/94296622

这是我的一项大作业，两篇博客加起来有写实验报告和代码，并有做PPT，下载链接见博客最后。

一、经典逻辑和模糊逻辑

如果想看模糊数学的数学干货讲义，强推这一PPT：Fuzzy Mathematics and Its in Technology，见博客最后的下载链接中：模糊系统/资料搜集/Fuzzy_Mathematics_and_Its_Importance_in.pptx

 经典逻辑（布尔逻辑）坚持所有事物（陈述）都可以用二元项（0或1，黑或白，是或否）来表达，而模糊逻辑用隶属度替代了布尔真值，允许在包含0和1之间的集合成员关系值。这些陈述表示实际上接近于日常人们的语意陈述，因为“隶属”在多数时候是部分的，非二元的，不精确的。

以星期四是周末吗？星期五是周末吗？这样的问题举个例子：

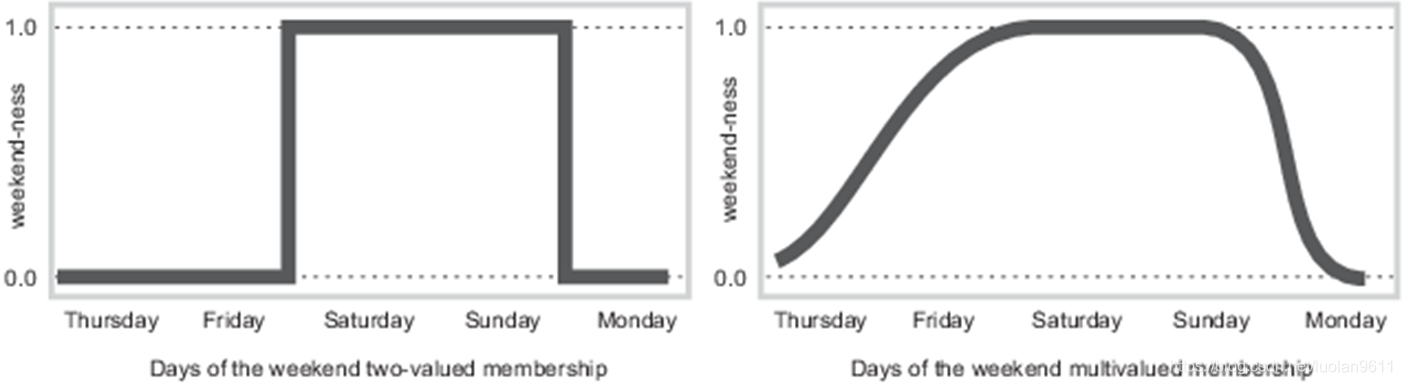
经典逻辑给出的回答：是（1）/不是（0），像下面的左图，星期五在凌晨的时候对这个问题的回答是1，所以有个阶跃。

模糊逻辑给出的回答：星期四好像不算周末吧，如果“是周末”得分为1的话，可能周四只有0.1的程度算是周末；周五算是周末的程度会高一些，虽然白天要上班但晚上就可以休息了呀，那给个0.8分好了，像下边的右图。

同样针对于常见的身高问题来说的话，身高高，身高低，不算很高，非常高，这一系列的表述不是简单的0和1能够表达的，这样的程度的概念具有一定的模糊性，因此需要模糊集，需要模糊逻辑。

模糊集：被定义为具有连续成员等级的一类对象。它的特征在于“隶属函数”或“特征函数”，隶属函数为模糊集的每个成员分配单位区间[0,1]中的隶属度，每个成员的隶属度构成了模糊集。

隶属函数（Membership functions）：隶属函数完全定义了模糊集，隶属函数提供元素与模糊集的相似程度的度量（隶属度），所有模糊集中的关键问题之一是如何