一般的运算放大器内部主要由差动输入级、增益级和输出级构成,此外还包括偏置电路。
差动输入级:
以一个差分放大器作为输入级,其模型如下:

我们定义:共模信号指的是两个电压或者电流的相同部分,表示为:
差模信号表示为:Vdiff = Vi1 - Vi2
理想差分放大器就是只放大差模信号,抑制共模信号,即:Vo = Ad(Vi1 - Vi2) = AdVdiff
但实际上共模信号仍会产生一个小的输出电压,即:Vo = AdVdiff + AcVcm
所以我们通过一个参数,共模抑制比(CMRR)来区分一个差分放大器的好坏,即看放大器能不能在接收到不同信号时提供高增益,接收到相同信号时提供低增益:
为什么要用差分放大器作为输入级呢?假设我们的输入交流信号为Vi1和Vi2(Vi2 = -Vi1),此时干扰信号为Vdisturb,因为被捕获的干扰信号在两个输入端一般是一致的,所以此时Vcm = (Vi1 + Vi2) / 2 + Vdisturb,而Vdiff仍为Vi1 - Vi2,我们放大差模信号,就可以避免噪声干扰。
举个例子,下面是一个长尾式差分放大电路:

对于Q1,Q2两个BJT的分析,可以详看:关于BJT三级管饱和区的分析-优快云博客
对于这个电路的交直流分析(模电),可以详看:电子电路:差分放大器分析-优快云博客
我们直接说结论:对于这个长尾式差分放大电路,其共模电压增益为,差模电压增益为
,其中ICQ为晶体管静态工作电流,这里我们就不详细分析如何增大其共模抑制比了。
经过这个差动输入级后,信号的差模部分得到放大,共模部分得到抑制,实现了提供高输入阻抗以及低噪声放大的功能。
偏置电路:
首先,我们需要知道一个概念:偏置电流。在这里我们提到的是输入偏置电流。可以看上面长尾式差分放大电路的例子,为了使两个BJT工作在放大区,基极必须提供一定的输入电流 IB(+) 与IB(-)。而对于FET构成的输入级来说,影响主要是漏电流,详细解释可以看:深度解析输入偏置电流和输入失调电流的定义来源以及对电路的影响-优快云博客。理想情况下,运放的输入端是没有电流存在的,但是为了保证放大器工作在线性区,或者需要ESD保护二极管,所以实际的运放可以视为一个理想运放与两个偏置电流源的组合:
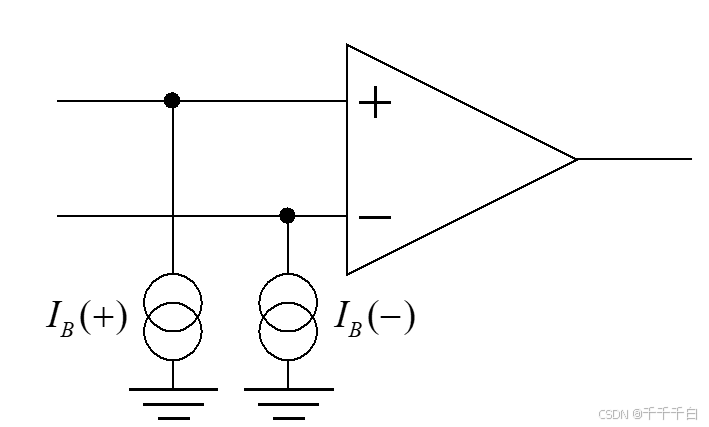
而由于元器件的差异,实际IB(+) 与 IB(-) 间也存在差异,因此我们定义:
输入偏置电流 (Input Bias Current):
输入失调/偏移电流 (Input Offset Current):
这个偏置电流与失调电流会导致放大器输出端出现一个与输入信号无关的电压称为失调/偏移电压 (Offset Voltage),我们应该最小化偏置电流与失调电流的影响。
目前了解的优化方法一共有两个:一个是输入端外部电路添加补偿电阻,使同相与反相输入端电阻相等,即:

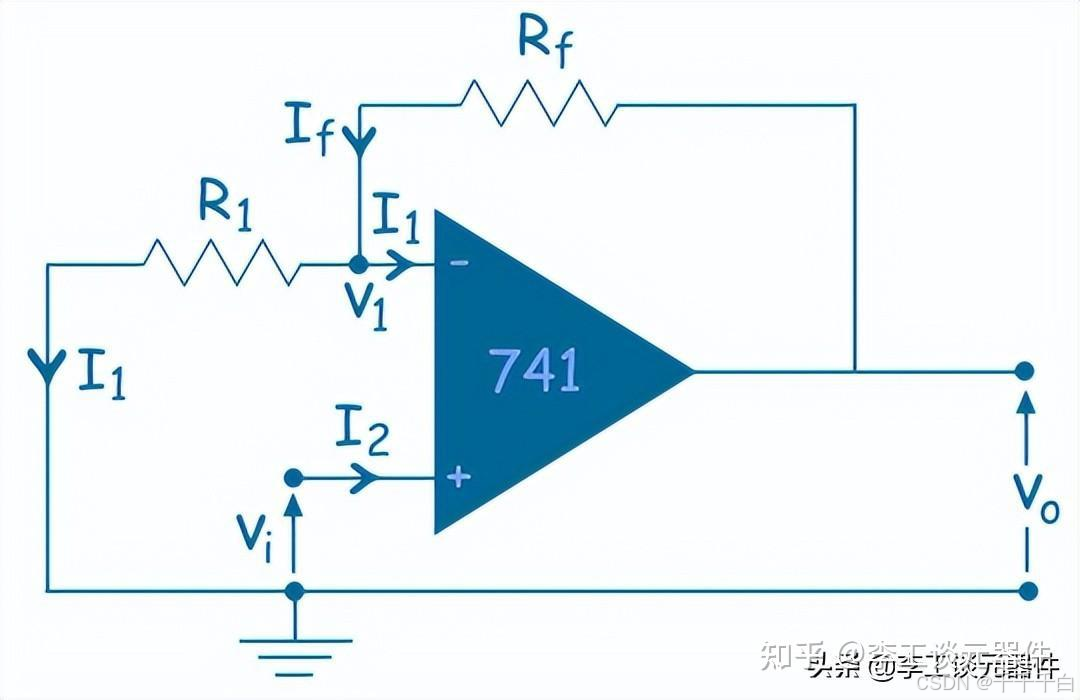
我们视Vin为短路,分别单独分析IB(+)和IB(-)的影响,可以得到ΔVo = (IB(+) - IB(-))Rf,即当IB(+) ≈ IB(-)时,偏置电流的影响可以忽略不计,这时主要影响就是失调电流。
第二个方法是内部偏置电流补偿,即用运放内部的偏置电路来消除影响:

上面741运放即利用镜像电流源(电流镜)来为运放的所有级提供偏置电流,确保晶体管工作在合适的区域。它可以动态消除输入级偏置电流的影响,始终维持一个合适的静态工作点。
增益级:
提供放大器的主要增益来源
输出级(暂不在这里分析)
在了解了一个运算放大器的基本结构后,我们来理解一下几个基本的运算放大器电路。
反相比例运放电路

我们假设这个图里最上方的两个电阻分别为R1, Rf,阻值为R/2的电阻为R2
理想情况下:
非理想情况下,即存在偏置电流(单独分析同相反相端偏置电流影响):
当时
证明了上面第一个优化方法的正确性
同相比例运放电路
相似的,我们假设同相输入端也有一个电阻R2
理想情况下:
非理想情况下,在分析偏置电流的影响时,我们会将输入端电压忽略,所以此时同相运放和反相运放在Vin = 0的情况下是相同的电路,因此:
此外,我们还可以根据A(放大系数)来分析一下该电路:
我们知道运放电路的闭环增益公式为:
这里Acl为闭环增益,Aol为开环增益,β为反馈系数,βAol为环路增益,理想情况下,开环增益为无穷大,其闭环增益即为反馈系数的倒数
当开环增益不为无穷大时,我们可以得到:
其中被定义为增益误差 (error)
积分电路
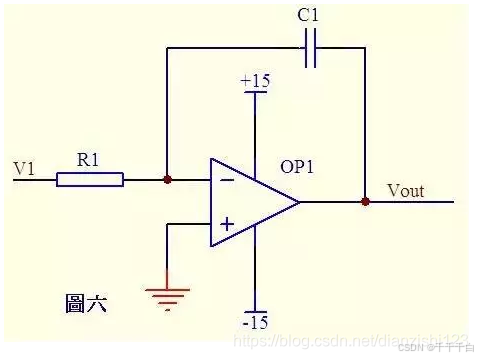
在这个电路中,我们假设同相输入端连接了一个电阻R2(图中未展示)
前面的学习中,我们了解了偏置电流与失调电流,所以在这里IB(+)与IB(-)还有另一种表示方式:
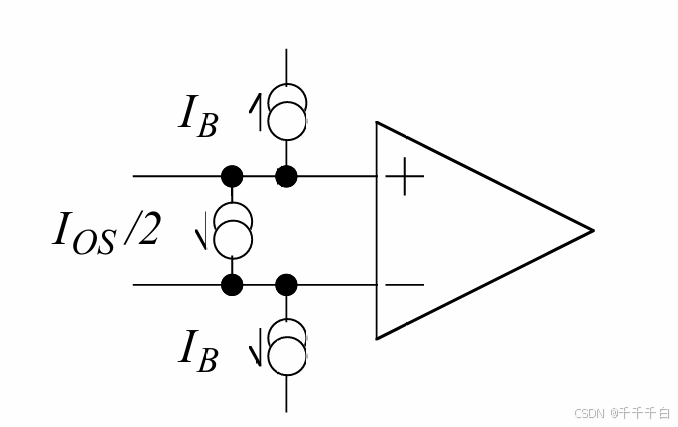
所以我们可以得到:
我们视后边的积分变量为该积分器的误差 (error),已知时间常数
在R2 = R1的情况下,简化该误差可以得到:
通过积分电路,我们进一步证明了使同相反相端输入电阻的相等的方法来减小偏置电流影响的可行性。
减法运算电路
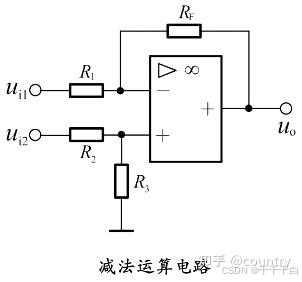
偏置电流与CMRR是两个相对独立的、共同会对运放的输出造成影响的参数,前面几个电路我们简单分析了偏置电流的影响,在这个减法运算电路中,我们主要考虑一下CMRR带来的误差。
首先,我们将这个电路的输出表示为:
Ad为差模增益,Ac为共模增益,Vdiff = ui1 - ui2,Vcm = (ui1 + ui2) / 2
在理想情况下,先单独看反相输入端,此时ui2我们视为0:
再单独看同相输入端,此时ui1为0:
即可得到:
通过这两个式子,我们就可以分析出CMRR以及后续电阻误差对输出带来的影响
仪表放大器
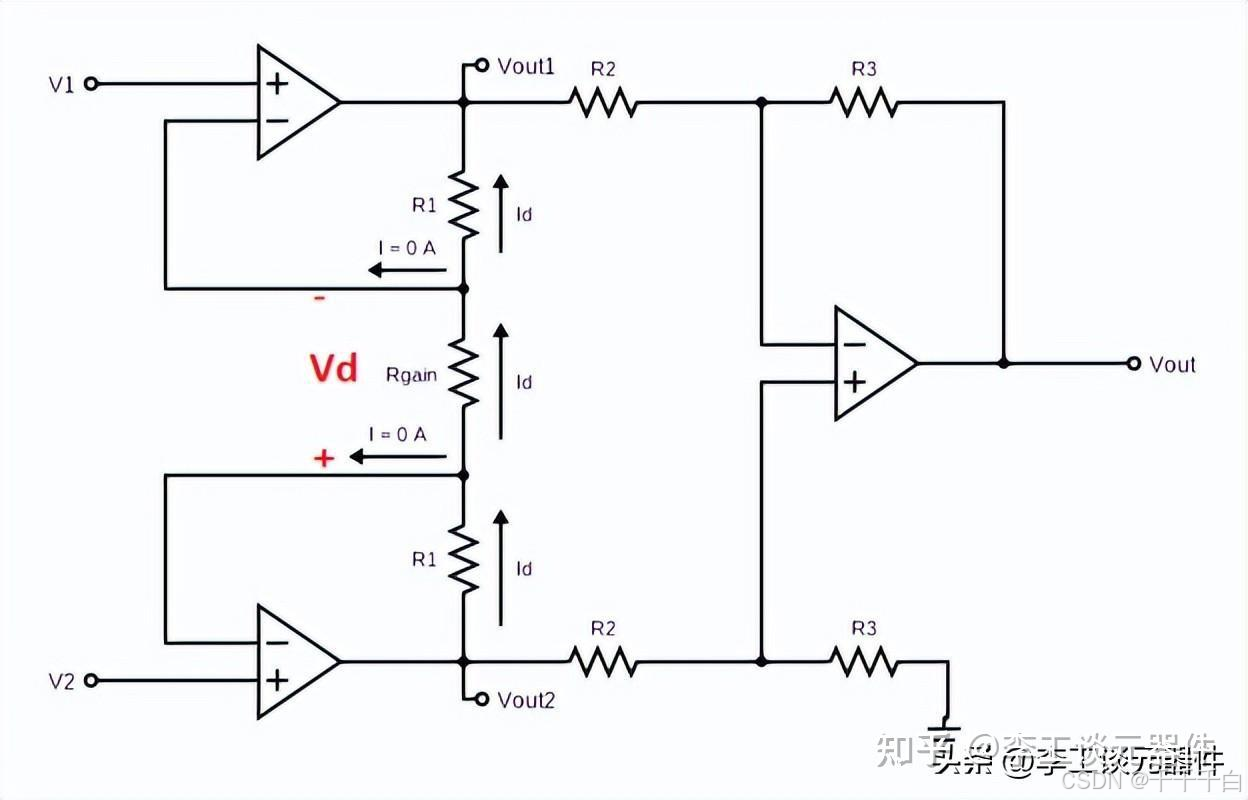
简单来说,仪表放大器就是由两个同相放大器和一个差分放大器构成的组合,对于第一级,也就是两个同相放大器的部分,假设忽略偏置电流的影响,理想情况下,,所以:
第二级,减法运算电路,上面我们知道:
带入这个电路:
仪表放大器具有具有高输入阻抗,良好的CMRR,低输入偏移,低输出阻抗等优点




















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








