算法拾遗二十一之图(一)
有向图和邻接表法
如下图:
a的邻居是b
b的邻居是c
c的邻居是a e f
e没有邻居
f的邻居是e
我们可以通过这种方式去描述一个图,同时也可以根据这个邻接表去表述这个边的权重。
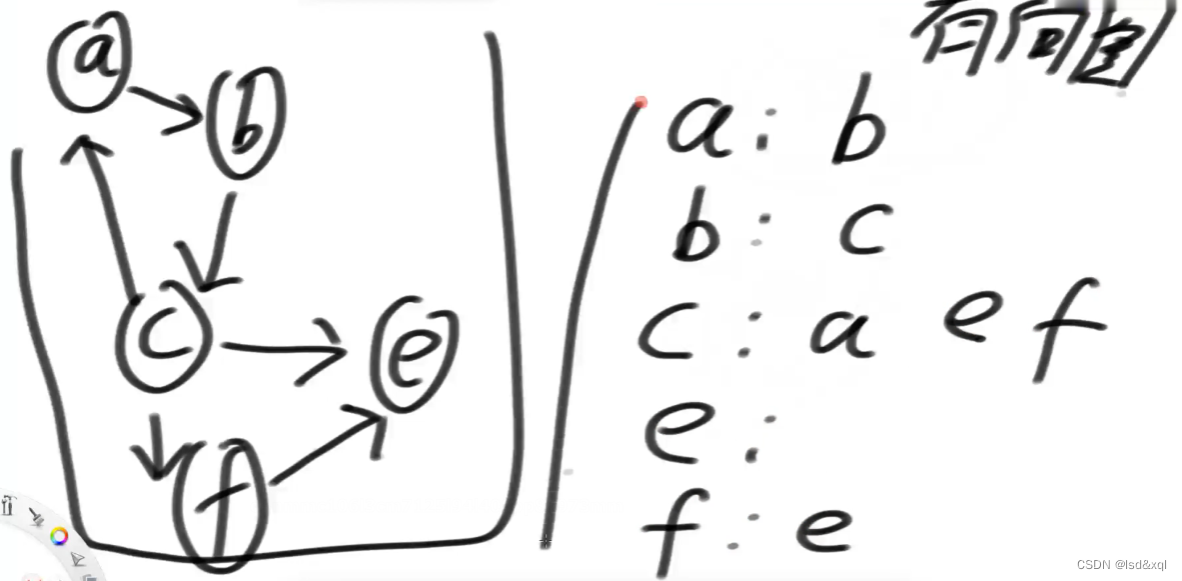
邻接矩阵法
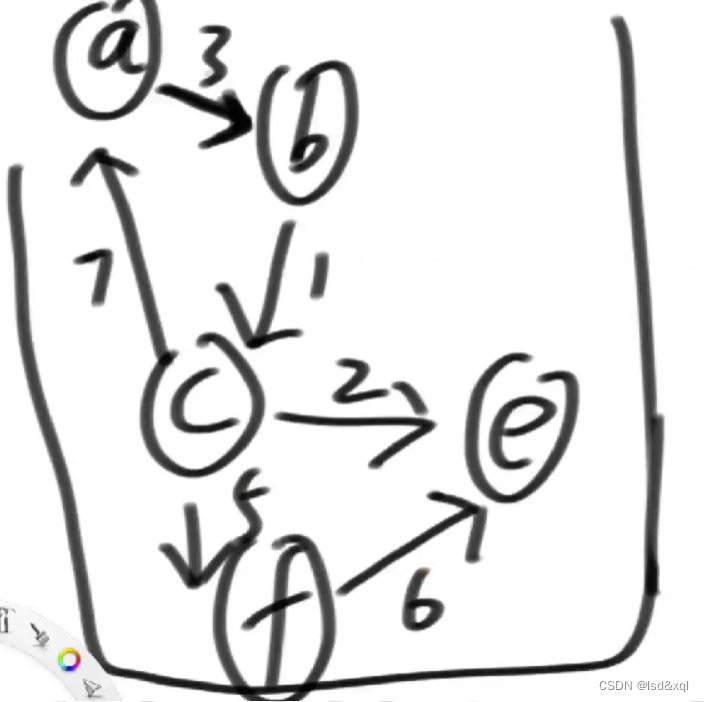
如上图:
可以通过如下矩阵去描述这张图,
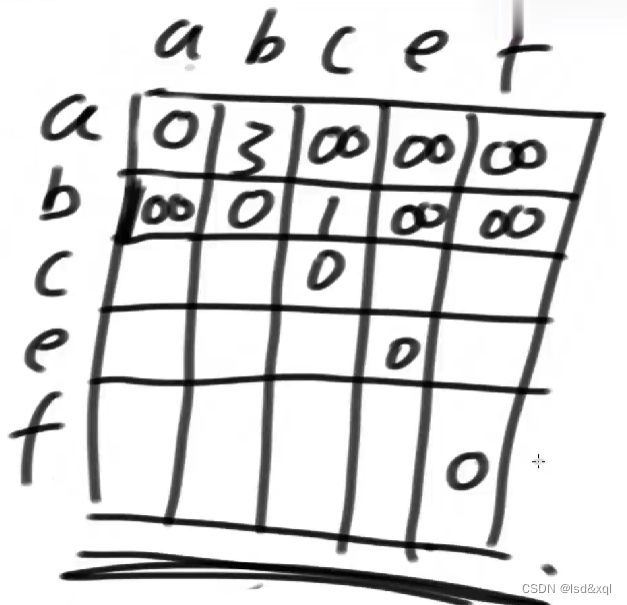
扩展图表述方式
当然最常遇到的图表达是这样的表达:
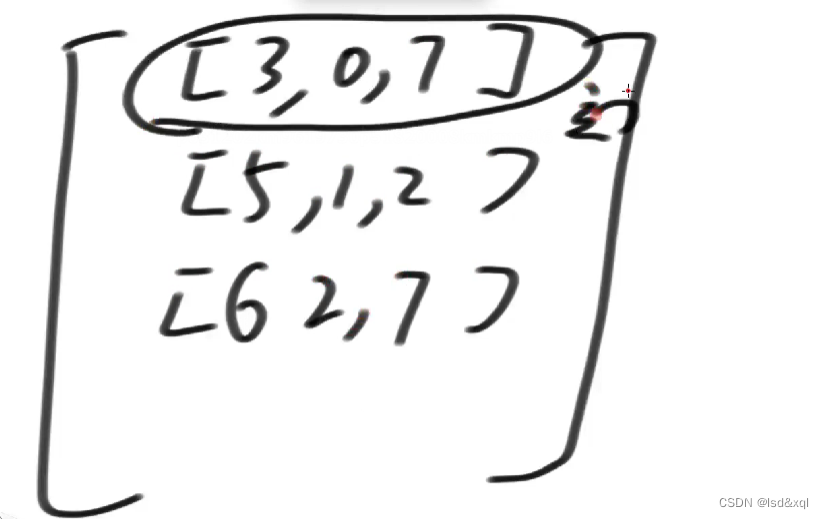
如上横排的一个数组代表一个边:
这个边权重是3,并且是从0到7的
第二个边权重是5,并且是从1到2的
第三个边权重是6,从2到7的
当然还有如下的表示方式:
这种方式表示的图为某个节点一直往外去指:
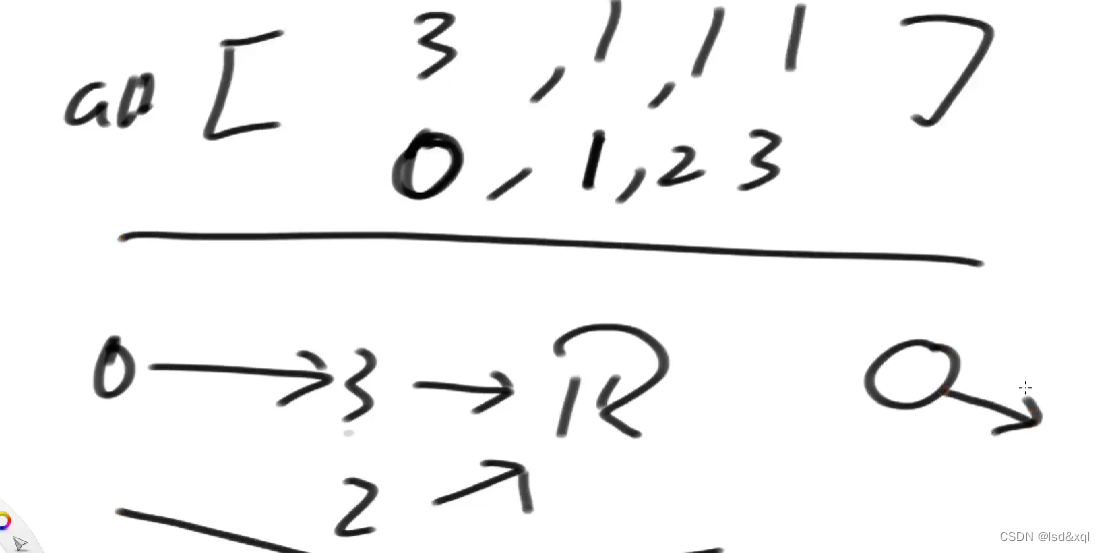
一般在做题过程中会遇到各种各样描述的图结构,此时就需要做一个专属于自己的图结果来将各种各样描述的图结构给做一个适配,从而来完成题解
点结构描述以及边结构描述图
// 点结构的描述
public class Node {
public int value;
//图的入度:被多少个点指向当前节点的
public int in;
//图的出度:当前节点指向别人的有多少条
public int out;
//有哪些邻居
public ArrayList<Node> nexts;
//从它出发有哪些直接的边
public ArrayList<Edge> edges;
public Node(int value) {
this.value = value;
in = 0;
out = 0;
nexts = new ArrayList<>();
edges = new ArrayList<>();
}
}
public class Edge {
//边的权重是多少
public int weight;
//从哪个点到哪个点的 from -> to
public Node from;
public Node to;
public Edge(int weight, Node from, Node to) {
this.weight = weight;
this.from = from;
this.to = to;
}
}
//图
public class Graph {
//用户给定一个值,然后再根据这个值去生成一个node做对应
public HashMap<Integer, Node> nodes;
public HashSet<Edge> edges;
public Graph() {
nodes = new HashMap<>();
edges = new HashSet<>();
}
}
如下图:
入度为2
出度为3
从它出发的邻居:6 7 8
从它出发的边:5-6、5-7、5-8
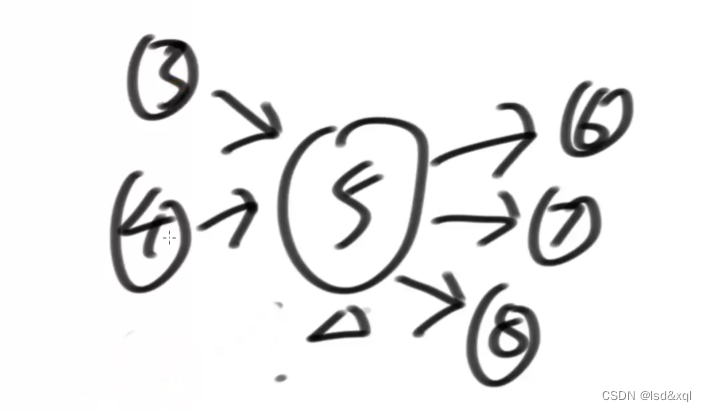
接口类将数组转化为图
public class GraphGenerator {
// matrix 所有的边
// N*3 的矩阵
// [weight, from节点上面的值,to节点上面的值]
//
// [ 5 , 0 , 7] 权重为5,是从0到7的路径
// [ 3 , 0, 1]
//
public static Graph createGraph(int[][] matrix) {
Graph graph = new Graph();
for (int i = 0; i < matrix.length; i++) {
// 拿到每一条边的权重, matrix[i]
int weight = matrix[i][0];
//获取从哪指向哪
int from = matrix[i][1];
int to = matrix[i][2];
//你的点集里面是否包含了from这个节点
if (!graph.nodes.containsKey(from)) {
//没包含则把这个from给建立出来
graph.nodes.put(from, new Node(from));
}
//你的点集里面是否包含了to这个节点
if (!graph.nodes.containsKey(to)) {
//没包含则把这个to给建立出来
graph.nodes.put(to, new Node(to));
}
//获取from和to的Node类型节点
Node fromNode = graph.nodes.get(from);
Node toNode = graph.nodes.get(to);
//建立新的from到to的边
Edge newEdge = new Edge(weight, fromNode, toNode);
//from点的直接邻居包含了to
fromNode.nexts.add(toNode);
//from点的出度应该加一个
fromNode.out++;
//to点的入度加一个
toNode.in++;
//from点出发直接的边加一个
fromNode.edges.add(newEdge);
//同时这个边是整个图的边集的一部分
graph.edges.add(newEdge);
}
return graph;
}
}
图的宽度优先遍历
宽度优先遍历
1,利用队列实现
2,从源节点开始依次按照宽度进队列,然后弹出
3,每弹出一个点,把该节点所有没有进过队列的邻接点放入队列
4,直到队列变空
注意因为图中存在回路所以通过set方式去实现
public class Code01_BFS {
// 从node出发,进行宽度优先遍历
public static void bfs(Node start) {
if (start == null) {
return;
}
Queue<Node> queue = new LinkedList<>();
HashSet<Node> set = new HashSet<>();
queue.add(start);
set.add(start);
while (!queue.isEmpty()) {
Node cur = queue.poll();
System.out.println(cur.value);
for (Node next : cur.nexts) {
//set中没有的才加入到队列中同时set集合更新
if (!set.contains(next)) {
set.add(next);
queue.add(next);
}
}
}
}
}
图的深度优先遍历
一条路没走完就走到死,走完了就逐渐往上看看哪个位置还没走完
1,利用栈实现
2,从源节点开始把节点按照深度放入栈,然后弹出
3,每弹出一个点,把该节点下一个没有进过栈的邻接点放入栈
4,直到栈变空
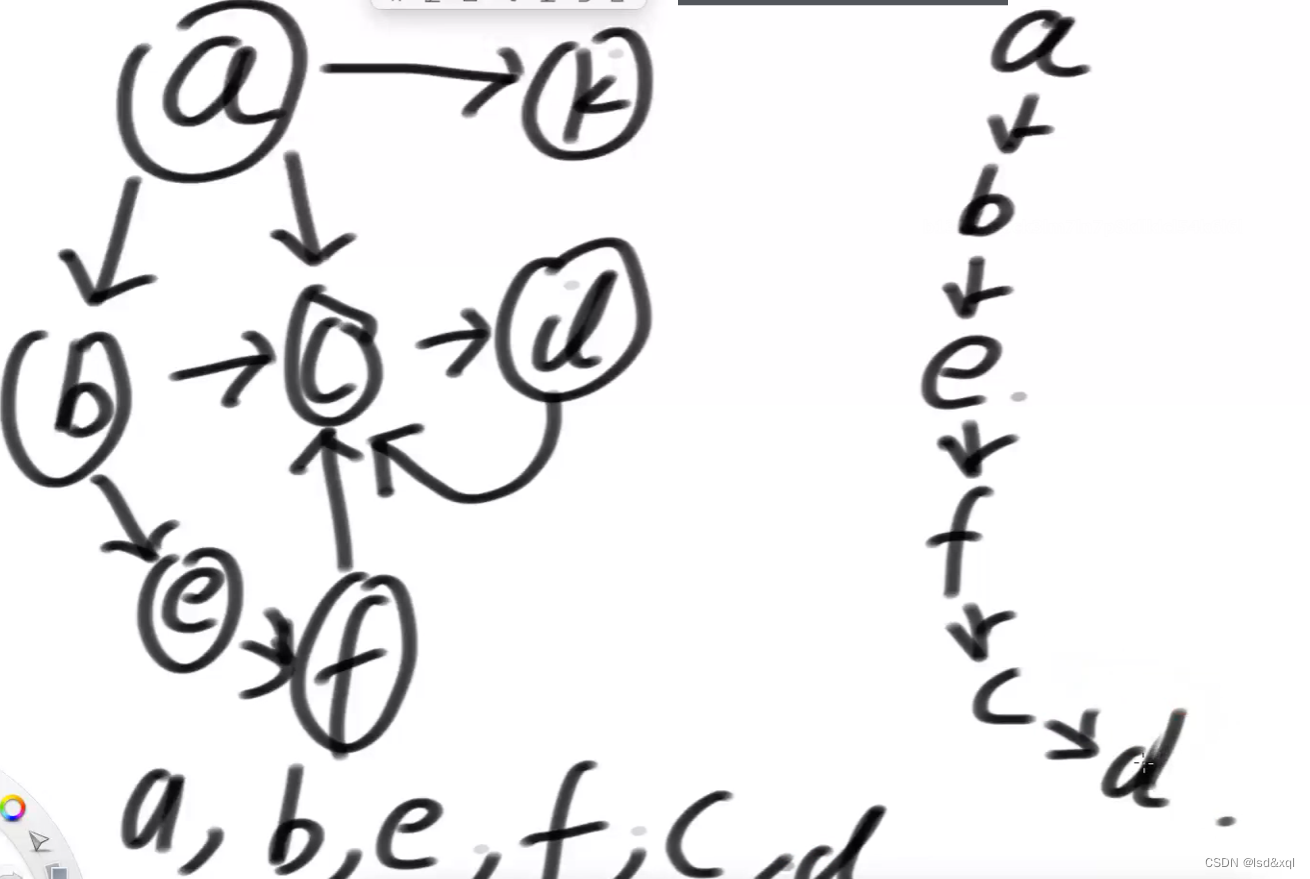
如上图首先从a出发可以依次走到【b,e,f,c,d】然后d有个回路到c,所以这第一步走完了,然后这条路往上弹,然后看c是否还有其他路可以走,发现没有往上弹到f,发现f的路也走完了,然后往上弹到e,发现路也走完了,然后往上弹到b,b还可以走到c但是发现c被走过了,只能再往上弹,到a的时候发现还可以走k那么走k,最后再看k有没有其他的路,k没有则弹出k,最后回到a发现a的所有路都被走过了,流程结束,此时结果为【a,b,e,f,c,d,k】
public class Code02_DFS {
public static void dfs(Node node) {
if (node == null) {
return;
}
//准备一个栈和一个set集合【防止回路】
Stack<Node> stack = new Stack<>();
HashSet<Node> set = new HashSet<>();
//将出发节点依次压栈和放入set里面
stack.add(node);
set.add(node);
//并打印当前入栈的值
System.out.println(node.value);
while (!stack.isEmpty()) {
//弹出栈顶元素并找它的邻居
Node cur = stack.pop();
for (Node next : cur.nexts) {
//如果set集合里面没有包含它的邻居
if (!set.contains(next)) {
//把当前节点压回去
stack.push(cur);
//将邻居也注册上
stack.push(next);
set.add(next);
//打印邻居
System.out.println(next.value);
//终止当前循环
break;
}
}
}
}
}
图的拓扑排序算法
1)在图中找到所有入度为0的点输出
2)把所有入度为0的点在图中删掉,继续找入度为0的点输出,周而复始
3)图的所有点都被删除后,依次输出的顺序就是拓扑排序
要求:有向图且其中没有环
应用:事件安排、编译顺序
public class Code03_TopologySort {
// directed graph and no loop
public static List<Node> sortedTopology(Graph graph) {
// key 某个节点 value 剩余的入度
HashMap<Node, Integer> inMap = new HashMap<>();
// 只有剩余入度为0的点,才进入这个队列
Queue<Node> zeroInQueue = new LinkedList<>();
//遍历图中所有的点
for (Node node : graph.nodes.values()) {
//然后将点对应的入度存入inMap
inMap.put(node, node.in);
//如果点的入度为0则放入zero的队列里面去
if (node.in == 0) {
zeroInQueue.add(node);
}
}
//拓扑排序的结果放入result
List<Node> result = new ArrayList<>();
while (!zeroInQueue.isEmpty()) {
//将zero队列中的元素弹出
Node cur = zeroInQueue.poll();
//将弹出的点放入result结果集里面
result.add(cur);
//消除当前弹出点的影响
for (Node next : cur.nexts) {
//当前点对应的所有邻居节点的入度全减去1
inMap.put(next, inMap.get(next) - 1);
//如果减去1之后邻居节点的入度为0则放入zero队列里面去
if (inMap.get(next) == 0) {
zeroInQueue.add(next);
}
}
}
return result;
}
}
拓展:
假设有x点和y点,假设从x走过的所有的路以及后面的路全都走过一遍后经历的点的数量为100【点次概念】,假设从y走过的所有的路以及后面的路全走过一遍后经历的点的数量为80,则x的拓扑序小于y【x的拓扑序一定在y前面】
为了防止找每个点都得去遍历它的后续所有节点,我们这里采用记忆化搜索。
// OJ链接:https://www.lintcode.com/problem/topological-sorting
public class Code03_TopologicalOrderDFS2 {
// 不要提交这个类
public static class DirectedGraphNode {
public int label;
public ArrayList<DirectedGraphNode> neighbors;
public DirectedGraphNode(int x) {
label = x;
neighbors = new ArrayList<DirectedGraphNode>();
}
}
// 提交下面的
public static class Record {
public DirectedGraphNode node;
//点次
public long nodes;
public Record(DirectedGraphNode n, long o) {
node = n;
nodes = o;
}
}
public static class MyComparator implements Comparator<Record> {
@Override
public int compare(Record o1, Record o2) {
return o1.nodes == o2.nodes ? 0 : (o1.nodes > o2.nodes ? -1 : 1);
}
}
public static ArrayList<DirectedGraphNode> topSort(ArrayList<DirectedGraphNode> graph) {
HashMap<DirectedGraphNode, Record> order = new HashMap<>();
for (DirectedGraphNode cur : graph) {
f(cur, order);
}
ArrayList<Record> recordArr = new ArrayList<>();
for (Record r : order.values()) {
recordArr.add(r);
}
//排序谁的点次高谁在前面
recordArr.sort(new MyComparator());
ArrayList<DirectedGraphNode> ans = new ArrayList<DirectedGraphNode>();
for (Record r : recordArr) {
ans.add(r.node);
}
return ans;
}
// 当前来到cur点,请返回cur点所到之处,所有的点次!
// 返回(cur,点次)
// 缓存!!!!!order
// key : 某一个点的点次,之前算过了!
// value : 点次是多少
public static Record f(DirectedGraphNode cur, HashMap<DirectedGraphNode, Record> order) {
if (order.containsKey(cur)) {
return order.get(cur);
}
// cur的点次之前没算过!
long nodes = 0;
//遍历所有的邻居获取邻居的点次
for (DirectedGraphNode next : cur.neighbors) {
nodes += f(next, order).nodes;
}
Record ans = new Record(cur, nodes + 1);
order.put(cur, ans);
return ans;
}
}
另一种思路,如果x的最大深度大于y那么x的拓扑排序小于y的拓扑排序:
// OJ链接:https://www.lintcode.com/problem/topological-sorting
public class Code03_TopologicalOrderDFS1 {
// 不要提交这个类【邻接表法】
public static class DirectedGraphNode {
//点的值是多少
public int label;
//有哪些直接邻居
public ArrayList<DirectedGraphNode> neighbors;
public DirectedGraphNode(int x) {
label = x;
neighbors = new ArrayList<DirectedGraphNode>();
}
}
// 提交下面的
public static class Record {
public DirectedGraphNode node;
public int deep;
public Record(DirectedGraphNode n, int o) {
node = n;
deep = o;
}
}
public static class MyComparator implements Comparator<Record> {
@Override
public int compare(Record o1, Record o2) {
return o2.deep - o1.deep;
}
}
public static ArrayList<DirectedGraphNode> topSort(ArrayList<DirectedGraphNode> graph) {
HashMap<DirectedGraphNode, Record> order = new HashMap<>();
for (DirectedGraphNode cur : graph) {
f(cur, order);
}
ArrayList<Record> recordArr = new ArrayList<>();
for (Record r : order.values()) {
recordArr.add(r);
}
recordArr.sort(new MyComparator());
ArrayList<DirectedGraphNode> ans = new ArrayList<DirectedGraphNode>();
for (Record r : recordArr) {
ans.add(r.node);
}
return ans;
}
public static Record f(DirectedGraphNode cur, HashMap<DirectedGraphNode, Record> order) {
if (order.containsKey(cur)) {
return order.get(cur);
}
//cur的点次之前没算过
int follow = 0;
//遍历所有邻居,收集邻居的深度最大值
for (DirectedGraphNode next : cur.neighbors) {
follow = Math.max(follow, f(next, order).deep);
}
//我的最大深度一定是再加一个
Record ans = new Record(cur, follow + 1);
order.put(cur, ans);
return ans;
}
}
最小树生成算法
Kruskal(要求无向图)
在不影响所有点都联通的情况下,所有边加起来最小的值是多少?算法的优劣与边有关
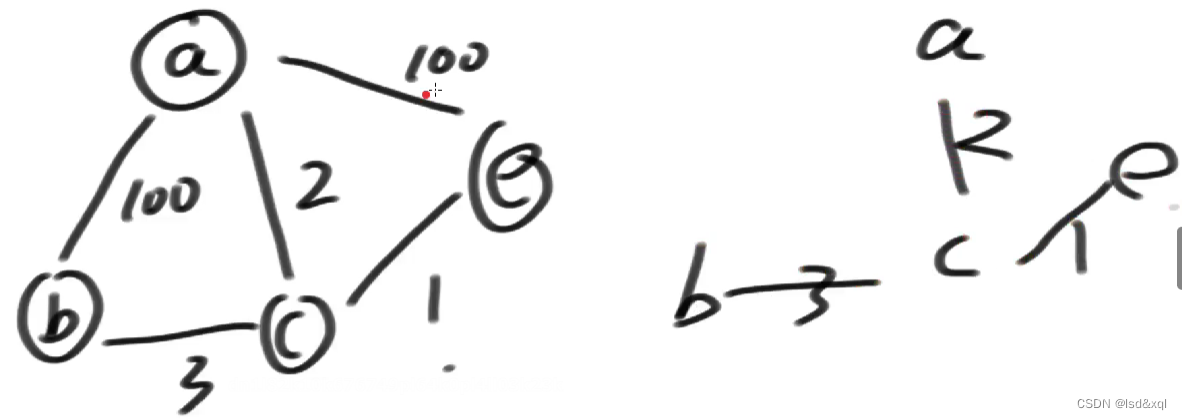
如上图右边部分整体权重为6为最小权重。
方法一(并查集):
1)总是从权值最小的边开始考虑,依次考察权值依次变大的边
2)当前的边要么进入最小生成树的集合,要么丢弃
3)如果当前的边进入最小生成树的集合中不会形成环,就要当前边
4)如果当前的边进入最小生成树的集合中会形成环,就不要当前边
5)考察完所有边之后,最小生成树的集合也得到了
注意:
成环的条件是判断并查集里面是否已经包含了两个节点【这两个节点已经指向了同一个代表节点】
//undirected graph only
public class Code04_Kruskal {
// Union-Find Set
public static class UnionFind {
// key 某一个节点, value key节点往上的节点
private HashMap<Node, Node> fatherMap;
// key 某一个集合的代表节点, value key所在集合的节点个数
private HashMap<Node, Integer> sizeMap;
public UnionFind() {
fatherMap = new HashMap<Node, Node>();
sizeMap = new HashMap<Node, Integer>();
}
public void makeSets(Collection<Node> nodes) {
fatherMap.clear();
sizeMap.clear();
for (Node node : nodes) {
fatherMap.put(node, node);
sizeMap.put(node, 1);
}
}
private Node findFather(Node n) {
Stack<Node> path = new Stack<>();
while(n != fatherMap.get(n)) {
path.add(n);
n = fatherMap.get(n);
}
while(!path.isEmpty()) {
fatherMap.put(path.pop(), n);
}
return n;
}
public boolean isSameSet(Node a, Node b) {
return findFather(a) == findFather(b);
}
public void union(Node a, Node b) {
if (a == null || b == null) {
return;
}
Node aDai = findFather(a);
Node bDai = findFather(b);
if (aDai != bDai) {
int aSetSize = sizeMap.get(aDai);
int bSetSize = sizeMap.get(bDai);
if (aSetSize <= bSetSize) {
fatherMap.put(aDai, bDai);
sizeMap.put(bDai, aSetSize + bSetSize);
sizeMap.remove(aDai);
} else {
fatherMap.put(bDai, aDai);
sizeMap.put(aDai, aSetSize + bSetSize);
sizeMap.remove(bDai);
}
}
}
}
public static class EdgeComparator implements Comparator<Edge> {
@Override
public int compare(Edge o1, Edge o2) {
return o1.weight - o2.weight;
}
}
public static Set<Edge> kruskalMST(Graph graph) {
UnionFind unionFind = new UnionFind();
unionFind.makeSets(graph.nodes.values());
// 从小的边到大的边,依次弹出,小根堆!
PriorityQueue<Edge> priorityQueue = new PriorityQueue<>(new EdgeComparator());
for (Edge edge : graph.edges) { // M 条边
priorityQueue.add(edge); // O(logM)
}
Set<Edge> result = new HashSet<>();
while (!priorityQueue.isEmpty()) { // M 条边
Edge edge = priorityQueue.poll(); // O(logM)
if (!unionFind.isSameSet(edge.from, edge.to)) { // O(1)
result.add(edge);
unionFind.union(edge.from, edge.to);
}
}
return result;
}
}
Prime算法
算法的优劣与点有关
1)可以从任意节点出发来寻找最小生成树
2)某个点加入到被选取的点中后,解锁这个点出发的所有新的边
3)在所有解锁的边中选最小的边,然后看看这个边会不会形成环
4)如果会,不要当前边,继续考察剩下解锁的边中最小的边,重复3)5)如果不会,要当前边,将该边的指向点加入到被选取的点中,重复2)
6)当所有点都被选取,最小生成树就得到了
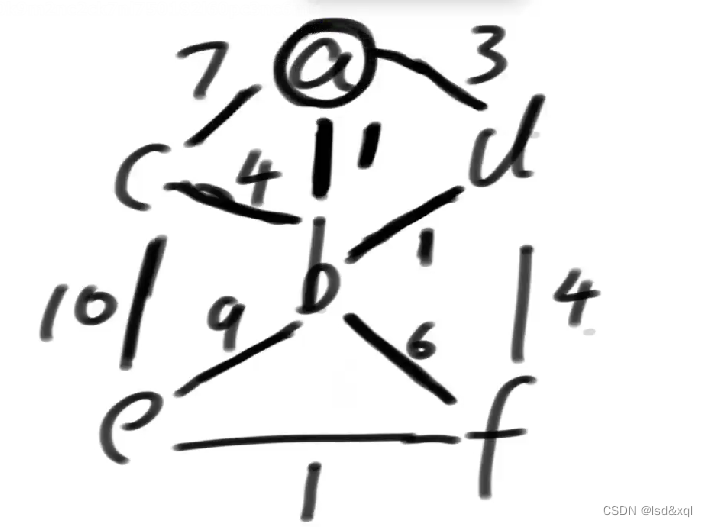
如上图假设从a出发,注意画圈的点是被解锁的点,往下如果边下面画了下划线就代表是一个待考虑的边,如果边上面画了勾则代表这个边被选上了,如果边上画了叉则代表不考虑当前边,如果这些符号都没有则是被锁住的边
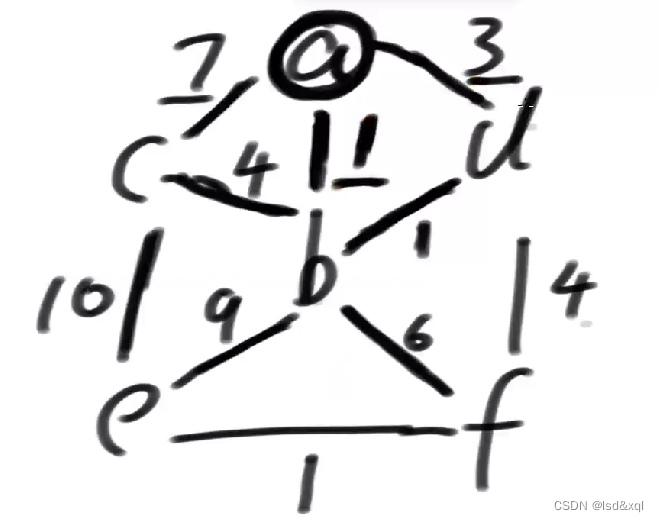
首先将7,1,3画线,可以认为除了画线的边考虑其他的边都不考虑,在所有可以考虑的边中选一个最小的,将1标记为勾
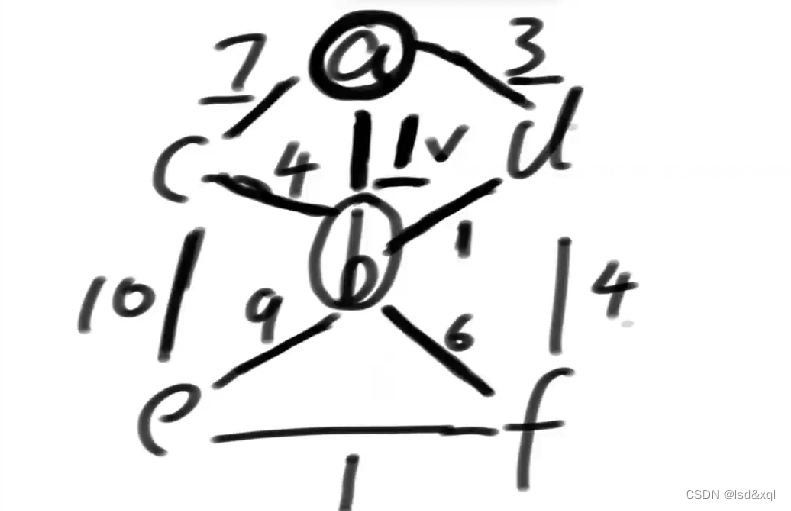
然后就可以解锁b了【从点去解锁边,然后再从边去解锁关联的点,再从点去解锁边,这样依次解锁下去】,b就可以解锁如下边了,然后就可以从下划线里面对应的边中去选了。
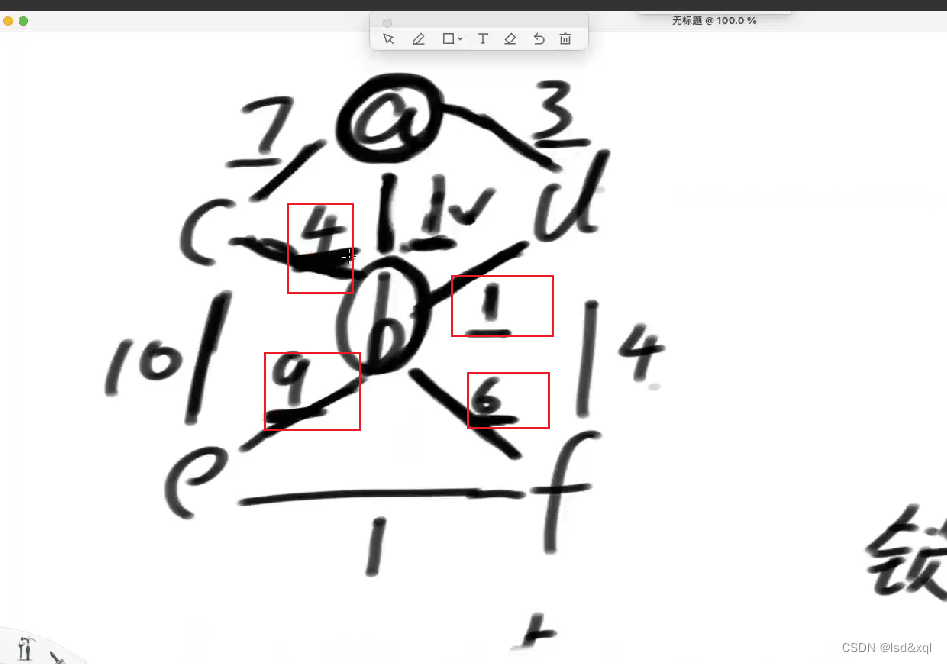
此时再选一个最小的权重为1的d,此时d再解锁权重为4的边
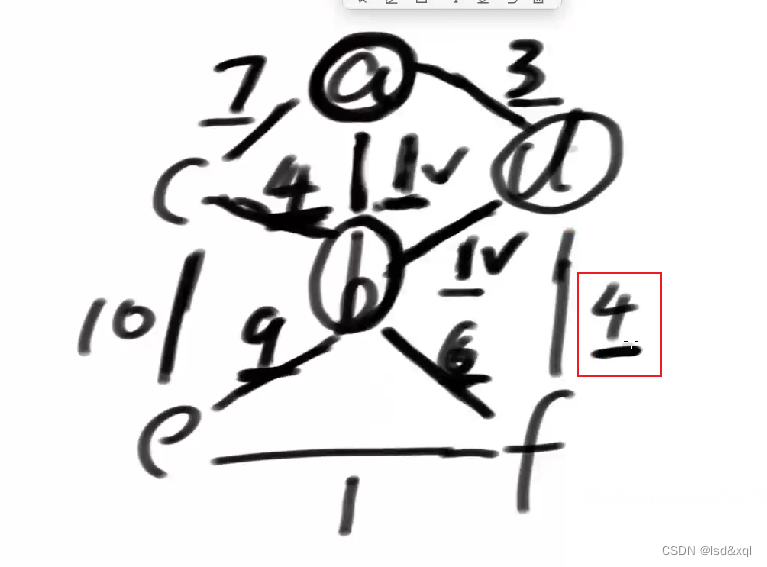
此时再选一个最小的3,但这个3对应的两个点都是解锁了的,所以对3画叉,表示可以不选3了
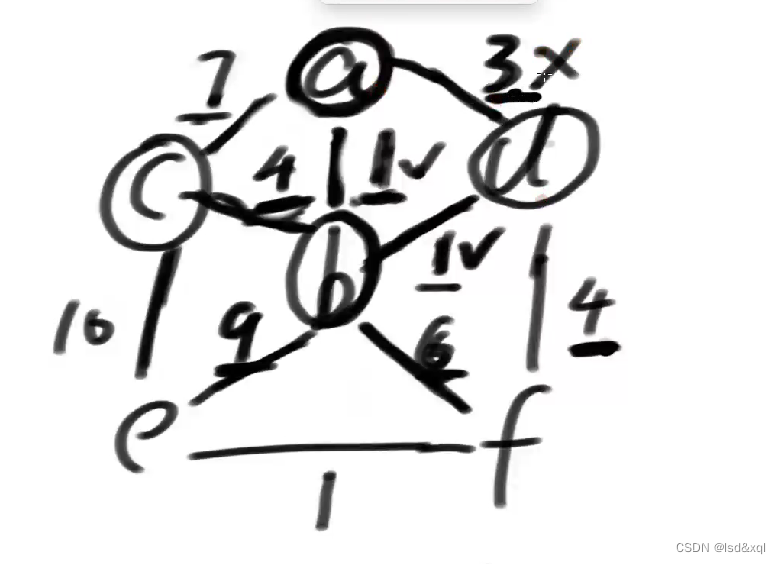
然后再选一个4
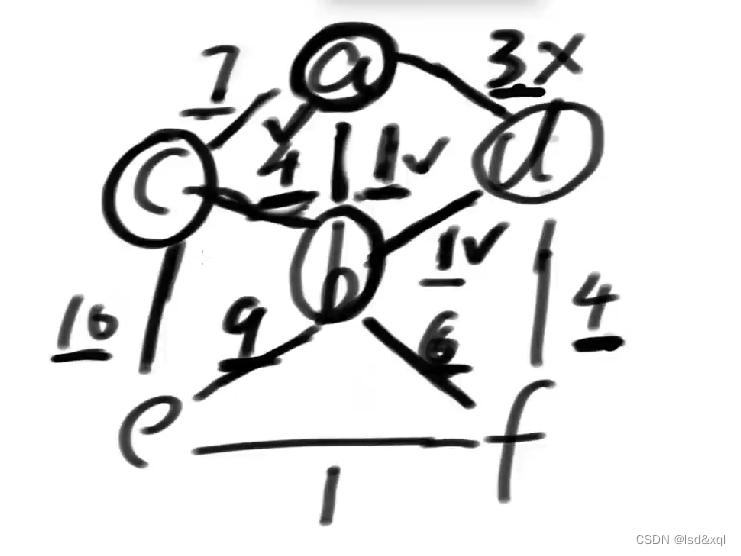
然后10也被解锁出来了,然后再选另一个4,然后f这个点就被解锁出来了,同时权重为1的ef的边也被解锁出来了。
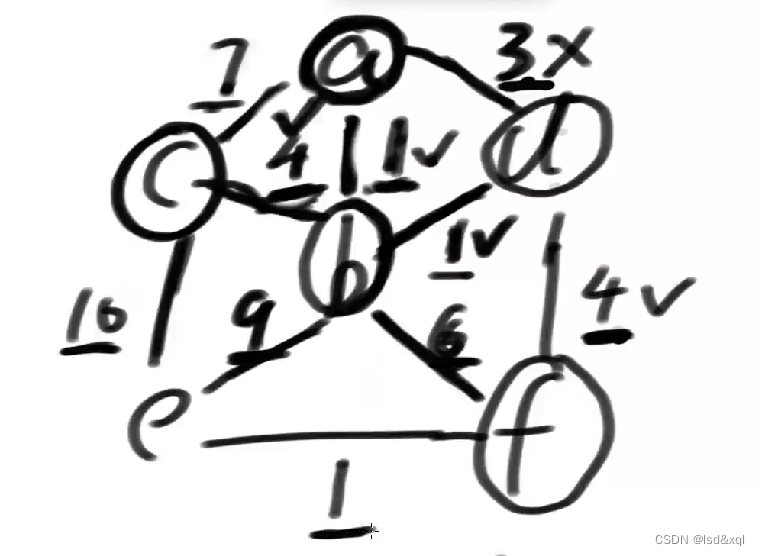
然后再选中1将e这个点也给拽进来,然后所有的点都被跑完了。
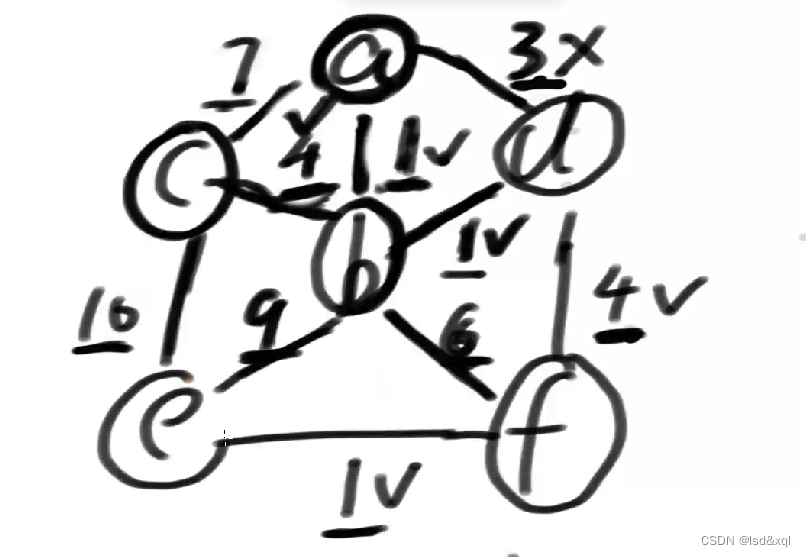
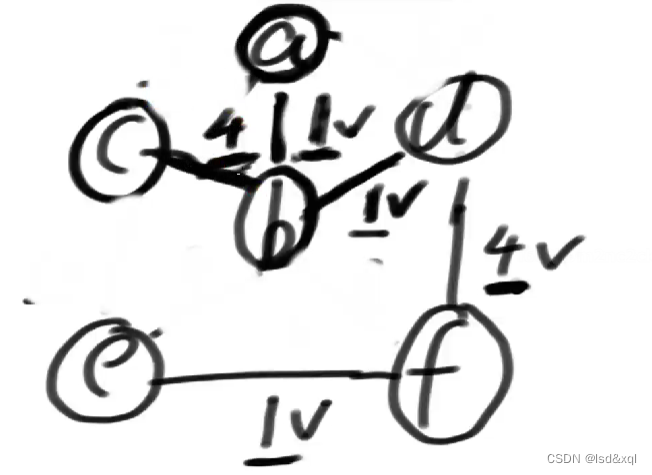
最终的结果为:
public static class EdgeComparator implements Comparator<Edge> {
@Override
public int compare(Edge o1, Edge o2) {
return o1.weight - o2.weight;
}
}
public static Set<Edge> primMST(Graph graph) {
// 解锁的边进入小根堆
PriorityQueue<Edge> priorityQueue = new PriorityQueue<>(new EdgeComparator());
// 哪些点被解锁出来了
HashSet<Node> nodeSet = new HashSet<>();
// 依次挑选的的边在result里
Set<Edge> result = new HashSet<>();
// 随便挑了一个点
for (Node node : graph.nodes.values()) {
// node 是开始点
if (!nodeSet.contains(node)) {
nodeSet.add(node);
// 由一个点,解锁所有相连的边
for (Edge edge : node.edges) {
priorityQueue.add(edge);
}
while (!priorityQueue.isEmpty()) {
// 弹出解锁的边中,最小的边
Edge edge = priorityQueue.poll();
// 可能的一个新的点
Node toNode = edge.to;
// 不含有的时候,就是新的点
if (!nodeSet.contains(toNode)) {
nodeSet.add(toNode);
result.add(edge);
for (Edge nextEdge : toNode.edges) {
priorityQueue.add(nextEdge);
}
}
}
}
// break;
}
return result;
}
Dijkstra算法
单元到某个点的路径是啥,指的是有向无负权重可以有环的图,同时也不能有整体环路为负数的环
1)Dijkstra算法必须指定一个源点
2)生成一个源点到各个点的最小距离表,一开始只有一条记录,即原点到自己的最小距离为0,源点到其他所有点的最小距离都为正无穷大
3)从距离表中拿出没拿过记录里的最小记录,通过这个点发出的边,更新源点到各个点的最小距离表,不断重复这一步
4)源点到所有的点记录如果都被拿过一遍,过程停止,最小距离表得到了
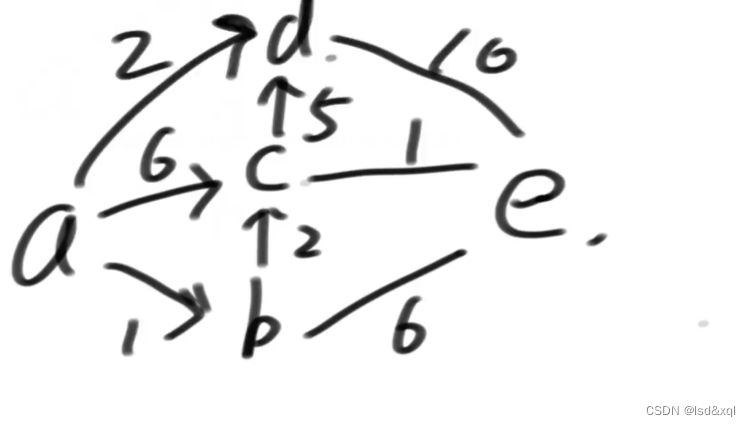
再维护一个距离表:
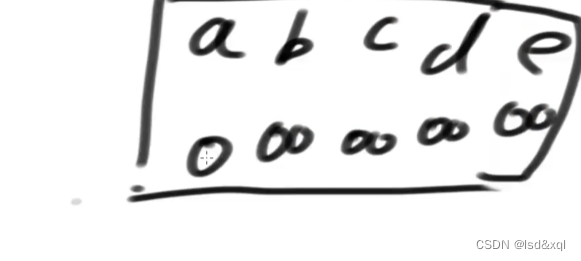
首先第一步:
已经确定的答案不碰,然后首先a:0出来了,然后a能达到的点有ab,ac,ad三条边,然后更新距离表:
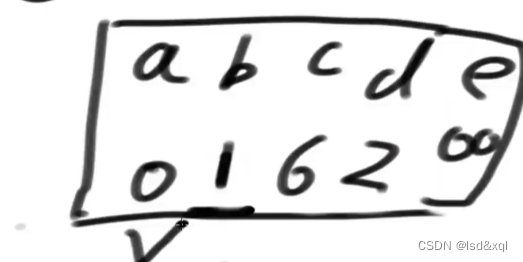
由于刚才弹出的是a->0的记录,所以画上对号,在没有画对号的记录中找到b:1最短,对应解锁的边为bc,be,然后由于经过
abe的距离比经过ae的短,所以更新e对应的距离为7,由于经过abc的距离比经过ac的短,所以更新c对应的值为3
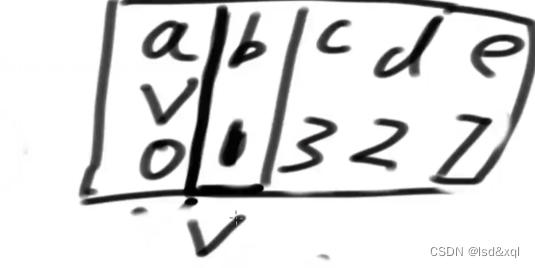
然后再在剩下的记录中弹出d:2,d对应的有个de长度为10,由于ade的长度为12大于距离表中到e的距离则不更新,然后锁住d点。
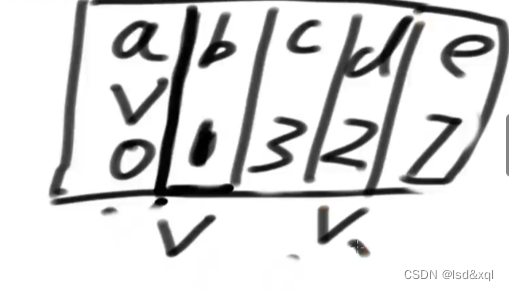
然后解锁c,a到c为3,发现c有ce这个边,到e的距离为1加上为4,更新距离表中e对应的值。
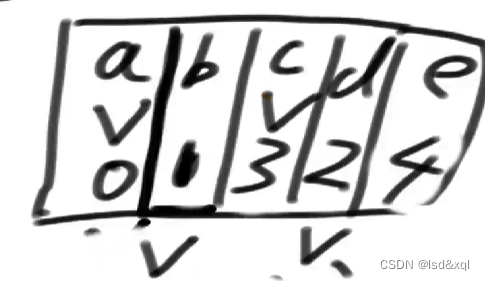
最后解锁e,发现e没有边则结束流程,最终得到的表返回为最后的答案。
public static HashMap<Node, Integer> dijkstra1(Node from) {
HashMap<Node, Integer> distanceMap = new HashMap<>();
distanceMap.put(from, 0);
// 打过对号的点
HashSet<Node> selectedNodes = new HashSet<>();
//第一步调用from出来
Node minNode = getMinDistanceAndUnselectedNode(distanceMap, selectedNodes);
while (minNode != null) {
// 原始点 -> minNode(跳转点) 最小距离distance
//原始点到跳转点的最小距离
int distance = distanceMap.get(minNode);
//跳转点有哪些边
for (Edge edge : minNode.edges) {
//每一条边去哪
Node toNode = edge.to;
if (!distanceMap.containsKey(toNode)) {
//原始点到跳转点的距离加上当前边的权重
distanceMap.put(toNode, distance + edge.weight);
} else {
// toNode已经存在,选最小值更新
distanceMap.put(edge.to, Math.min(distanceMap.get(toNode), distance + edge.weight));
}
}
//跳转点使命完成,则锁定当前跳转点
selectedNodes.add(minNode);
//再选择一个minNode出来执行上述流程
minNode = getMinDistanceAndUnselectedNode(distanceMap, selectedNodes);
}
return distanceMap;
}
/**
* distanceMap中哪个记录最小,而且不能是打过对号的点,此方式慢就慢在这个方法,需要用到
* 前面所学的加强堆
* @param distanceMap
* @param touchedNodes
* @return
*/
public static Node getMinDistanceAndUnselectedNode(HashMap<Node, Integer> distanceMap, HashSet<Node> touchedNodes) {
Node minNode = null;
int minDistance = Integer.MAX_VALUE;
for (Entry<Node, Integer> entry : distanceMap.entrySet()) {
Node node = entry.getKey();
int distance = entry.getValue();
if (!touchedNodes.contains(node) && distance < minDistance) {
minNode = node;
minDistance = distance;
}
}
return minNode;
}






















 991
991

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








