数据结构与算法拾遗六

最新推荐文章于 2025-07-02 19:15:25 发布

原创最新推荐文章于 2025-07-02 19:15:25 发布 · 170 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#java #leetcode #开发语言

算法块专栏收录该内容

73 篇文章

订阅专栏

数据结构与算法拾遗六

返回一棵树的最大深度

https://leetcode.cn/problems/maximum-depth-of-binary-tree

	public static class TreeNode {
		public int val;
		public TreeNode left;
		public TreeNode right;
	}

	// 以root为头的树，最大高度是多少返回！
	public static int maxDepth(TreeNode root) {
		if (root == null) {
			return 0;
		}
		//找左树和右树的最大高度并加上它自己
		return Math.max(maxDepth(root.left), maxDepth(root.right)) + 1;
	}

用先序数组和中序数组重建一棵树

https://leetcode.cn/problems/construct-binary-tree-from-preorder-and-inorder-traversal

先序数组和中序数组无重复值

则需要建出整棵树返回
如有如下先序和中序遍历顺序：
1，2，3，4，5，6，7
3，2，4，1，6，5，7
则我们首先可以确定根节点为1
然后根据根节点划分出中序遍历的左子树为
3，2，4
先序遍历的左子树为
2，3，4
然后再根据左子树划分出根节点
让上一次head的左指针指向当前左子树的根节点，找完以后让当前的2指向3，
然后再回到
3，2，4 中序
2，3，4 先序
找它的右子树，依次这样划分下去

代码如下所示：

   public static class TreeNode {
        int val;
        TreeNode left;
        TreeNode right;

        TreeNode(int val) {
            this.val = val;
        }
    }


    //利用中序和先序把整棵树返回
    public static TreeNode buildTree(int[] pre, int[] in) {
        if (pre == null || in == null || pre.length != in.length) {
            return null;
        }

        return f(pre, 0, pre.length - 1, in, 0, in.length - 1);
    }

    //有一棵树，先序结果是pre[L1,,,R1],中序结果是in[L2...R2]
    //建出整棵树返回头节点
    public static TreeNode f(int[] pre, int L1, int R1, int[] in, int L2, int R2) {
        //不是一个有效的范围，返回一个空树
        //例如一棵树只有一个分支先序遍历为 1，2，3
        //中序遍历为1，2，3
        //此时的find和L2是相等的，此时没有任何数字对应（撞上了树的空节点）
        if (L1 > R1) {
            return null;
        }
        TreeNode head = new TreeNode(pre[L1]);

        if (L1 == R1) {
            return head;
        }
        int find = L2;
        //找到头节点的值
        while (in[find] != pre[L1]) {
            find++;
        }
        //中序遍历 左树是L2到find-1的范围
        //先序遍历 左树是L1+find-L2
        head.left = f(pre, L1 + 1, L1 + find - L2, in, L2, find - 1);
        head.right = f(pre, L1 + find - L2 + 1, R1, in, find + 1, R2);
        return head;
    }

下面来优化：
由于上面的方法每次递归调用的时候都需要去遍历查找那么我们这里采用hash来做一个优化

   //利用中序和先序把整棵树返回
    public static TreeNode buildTree2(int[] pre, int[] in) {
        if (pre == null || in == null || pre.length != in.length) {
            return null;
        }

        HashMap<Integer,Integer>valueIndexMap = new HashMap<>(in.length);
        for(int i=0;i<in.length;i++) {
            valueIndexMap.put(in[i],i);
        }
        return g(pre, 0, pre.length - 1, in, 0, in.length - 1,valueIndexMap);
    }

    private static TreeNode g(int[] pre, int L1, int R1, int[] in, int L2, int R2, HashMap<Integer, Integer> valueIndexMap) {
        if(L1>R1) {
            return null;
        }
        TreeNode head = new TreeNode(pre[L1]);
        if(L1==R1) {
            return head;
        }
        //中序遍历等于根节点的位置
        int find = valueIndexMap.get(pre[L1]);
        head.left = g(pre,L1+1,L1+find-L2,in,L2,find-1,valueIndexMap);
        head.right = g(pre,L1+find-L2+1,R1,in,find+1,R2,valueIndexMap);

        return head;
    }

如上时间复杂度为O(n)有多少个节点则n这个函数调用多少次，每次进入g函数都是一个O(1)的操作。那么n次则是O(n)

107. 二叉树的层序遍历 II

题目链接：
https://leetcode.cn/problems/binary-tree-level-order-traversal-ii/
思路：
先将头节点放入队列中，然后依次去找头节点的左子树和右子树的头节点，
再依次将这些节点放入队列中，然后再逐步的找下去就是最终的结果。
这里采用LinkedList的用意是此数据结构增删比较快。

	public static class TreeNode {
		public int val;
		public TreeNode left;
		public TreeNode right;

		TreeNode(int val) {
			this.val = val;
		}
	}

	public List<List<Integer>> levelOrderBottom(TreeNode root) {
		List<List<Integer>> ans = new LinkedList<>();
		if (root == null) {
			return ans;
		}
		Queue<TreeNode> queue = new LinkedList<>();
		queue.add(root);
		while (!queue.isEmpty()) {
			int size = queue.size();
			List<Integer> curAns = new LinkedList<>();
			for (int i = 0; i < size; i++) {
				TreeNode curNode = queue.poll();
				curAns.add(curNode.val);
				if (curNode.left != null) {
					queue.add(curNode.left);
				}
				if (curNode.right != null) {
					queue.add(curNode.right);
				}
			}
			ans.add(0, curAns);
		}
		return ans;
	}

补充知识：
栈的实现还可以采用LinkedList和数组

//栈的实现还可以采用双端队列LinkedList，不过没有栈快
LinkedList<Integer> stack = new LinkedList<>();
stack.addLast(1);
stack.addLast(2);
stack.addLast(3);
while(!s.isEmpty()) {
System.out.println(s.pollLast());
}

//最快的是如下,前提栈是知道大小的，直接操作数组
int[] sta = new int[100];
int index = 0;
sta[index++] = 1;
sta[index++] = 2;
sta[index++] = 3;
System.out.println(sta[--index]);
System.out.println(sta[--index]);
System.out.println(sta[--index]);

判断是否为平衡二叉树

题目链接： https://leetcode.cn/problems/balanced-binary-tree

平衡二叉树概念：
每一棵子树的左数高度减右树高度的绝对值是否小于等于1

思路：
首先确定左树是平衡树，再确定右树也是平衡树，如果都确定好了以后，则比较左数和右树的高度差（如果差值绝对值都小于等于1则是平衡二叉树）。

public static class TreeNode {
		public int val;
		public TreeNode left;
		public TreeNode right;

		TreeNode(int val) {
			this.val = val;
		}
	}
	//以某个节点为头的时候，1）整棵树是否平 2）整棵树的高度是什么
	public static class Info {
		public boolean isBalanced;
		public int height;

		public Info(boolean i, int h) {
			isBalanced = i;
			height = h;
		}
	}

	public static boolean isBalanced(TreeNode root) {
		return process(root).isBalanced;
	}

	public static Info process(TreeNode root) {
		if (root == null) {
			return new Info(true, 0);
		}
		//左树是否平衡，左树高度
		Info leftInfo = process(root.left);
		//右树是否平衡，右树高度
		Info rightInfo = process(root.right);
		int height = Math.max(leftInfo.height, rightInfo.height) + 1;
		boolean isBalanced = leftInfo.isBalanced && rightInfo.isBalanced
				&& Math.abs(leftInfo.height - rightInfo.height) < 2;
		return new Info(isBalanced, height);
	}

判断一棵树是否为搜索二叉树？

对于每颗子树来说，左数的节点都小于其对应的根节点，右树的值都大于其对应的根节点
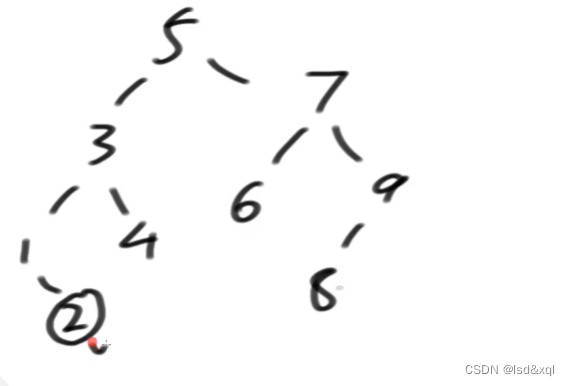
在这里插入图片描述
思路：
1、可以通过中序遍历来得到（如果中序遍历严格递增则是搜索二叉树）
2、递归(判断左子树是否是搜索二叉树，再判断右子树是否是搜索二叉树，并返回整个树的最大值和整个树的最小值)

    public static class TreeNode {
        public int val;
        public TreeNode left;
        public TreeNode right;

        public TreeNode(int val) {
            this.val = val;
        }
    }

    public static class Info {
        public boolean isBST;
        public int max;
        public int min;

        public Info(boolean isBST, int max, int min) {
            this.isBST = isBST;
            this.max = max;
            this.min = min;
        }
    }


    public static Info process(TreeNode x) {
        if (x == null) {
            //此处不能为负数，如果根节点是个负数则不能返回0
            //return new Info(true,0,0);
            //此处返回空
            return null;
        }
        //收集左右子树的信息
        Info leftInfo = process(x.left);
        Info rightInfo = process(x.right);
        //将当前点的值设置为max和min
        int max = x.val;
        int min = x.val;
        //如果收集的左子树信息不为空
        if (leftInfo != null) {
            max = Math.max(leftInfo.max, max);
            min = Math.min(leftInfo.min, min);
        }
        //如果收集的左子树信息不为空
        if (rightInfo != null) {
            max = Math.max(rightInfo.max, max);
            min = Math.min(rightInfo.min, min);
        }

        boolean isBST = true;
        if (leftInfo != null && !leftInfo.isBST) {
            isBST = false;
        }
        if (rightInfo != null && !rightInfo.isBST) {
            isBST = false;
        }

        //left Max <x right min>x （左子树的最大值要小于x，右子树的最小值要大于x）
        boolean leftMaxLessX = leftInfo == null ? true : (leftInfo.max < x.val);

        boolean rightMinMoreX = rightInfo == null ? true : (rightInfo.min > x.val);

        if (!(leftMaxLessX && rightMinMoreX)) {
            isBST = false;
        }

            return new Info(isBST, max, min);
    }

判断是否为平衡搜索二叉树（将两个方法做一个与运算即可得到）

112. 路径总和

题目链接：https://leetcode.cn/problems/path-sum/
思路：
将树的各个节点分叶子节点和非叶子节点来进行不同的处理，如果是非叶子节点就将当前的值加入到presum里面，如果是叶子节点则做比较
代码如下：

 public static class TreeNode {
        public int val;
        public TreeNode left;
        public TreeNode right;

        TreeNode(int val) {
            this.val = val;
        }
    }

    public static boolean isSum = false;

    public static boolean hasPathSum(TreeNode root, int sum) {
        if (root == null) {
            return false;
        }
        isSum = false;
        process(root, 0, sum);
        return isSum;
    }

    private static void process(TreeNode x, int preSum, int sum) {
        //当前x为叶子节点的时候则收集前面非叶子节点的值
        if (x.left == null && x.right == null) {
            boolean cur = x.val + preSum == sum;
            if (cur) {
                isSum = true;
            }
        }

        //x是非叶节点
        //加上自己的值并往下传
        preSum += x.val;
        if (x.left != null) {
            process(x.left, preSum, sum);
        }
        if (x.right != null) {
            process(x.right, preSum, sum);
        }


    }

113. 路径总和 II

思路：
每次递归的时候都做一个path来存储当前访问到树节点的路径，当访问到叶子节点的时候，则将叶子节点的值和路径和拿出来相加，如果相等的话，就可以通过path路径加上当前叶子节点的路径去得到最终的路径信息。
题目链接：https://leetcode.cn/problems/path-sum-ii/

 public static class TreeNode {
        public int val;
        public TreeNode left;
        public TreeNode right;

        TreeNode(int val) {
            this.val = val;
        }
    }

    public static List<List<Integer>> pathSum(TreeNode root, int sum) {
        List<List<Integer>> ans = new ArrayList<>();
        if (root == null) {
            return ans;
        }
        ArrayList<Integer> path = new ArrayList<>();
        process(root, path, 0, sum, ans);
        return ans;
    }



    public static void process(TreeNode x, List<Integer> path, int preSum, int sum, List<List<Integer>> ans) {
        if (x.left == null && x.right == null) {
            if (preSum + x.val == sum) {
                path.add(x.val);
                ans.add(copy(path));
                path.remove(path.size()-1);
            }
            return;
        }
        //x 非叶子节点
        path.add(x.val);
        preSum += x.val;
        if(x.left != null) {
            process(x.left,path,preSum,sum,ans);
        }
        if(x.right!=null) {
            process(x.right,path,preSum,sum,ans);
        }
        //从根节点的左子树返回到根节点的右子树，需要把左子树的根节点去掉，只保留最上层的根节点
        path.remove(path.size()-1);
    }
    public static List<Integer> copy(List<Integer> path) {
        List<Integer> ans = new ArrayList<>();
        for (Integer num : path) {
            ans.add(num);
        }
        return ans;
    }