数据结构与算法拾遗四

位图

位图的功能：
如果数字范围是确定的，那么就可以做出一个集合来告诉你数字是否存在。
位图的好处：
能够极大的压缩空间，比如说我的数字范围确定是0-31的范围，那么我就可以用一个int来表示出来这个范围int 为4字节32位。
如果要表示 -10到10，则可以转换为0-20的范围。

位图的实现

private long[] bits;//注意此处是一个非包装类long[],初始化时里面的值为0
public BitMap(int max) {
// 等价于(max+64)/64, 根据max加六十四来确定这个long[]里面应该放多少个数才能确定范围（说明：0<=max<=63 则只需要数组里面有一个数则可以表示如上范围）
bits = new long[(max + 64) >> 6];
}
如上相当于扣一个边界
bits数组初始化后则可以加数据了

1、位图里面加元素
让要加的数据除以64则能知道要加的数据在数组里的哪一个数里面，
如果要知道要加的这个数在这个数组里面哪个数的哪一位上面则取模

public void add(int num) {
// num/64 ->定位到属于数组的哪个位置
// num%64 则就等于 num&63
，因为num%64就相当于只保留后七位的数字，
如0110110110 模64就相当于 取得后七位 0110110
这个结果也相当于与上63，直接保留最后七位就好了

bits[num>>6] |= (1L<<(num&63))//此处相当于把这个1向左移动取余后得位
然后再和bits[index] 的值相或则赋值到bits[index]上面的对应位上了。
}

2、位图里面删元素
找到那个数对应的位上，然后把那个位标0；
比如说我们的数是第一排的数，然后要对三位置上面的数标0，则可以初始化
一个数左移三位然后取反最后再做与运算则能拿到最后的结果

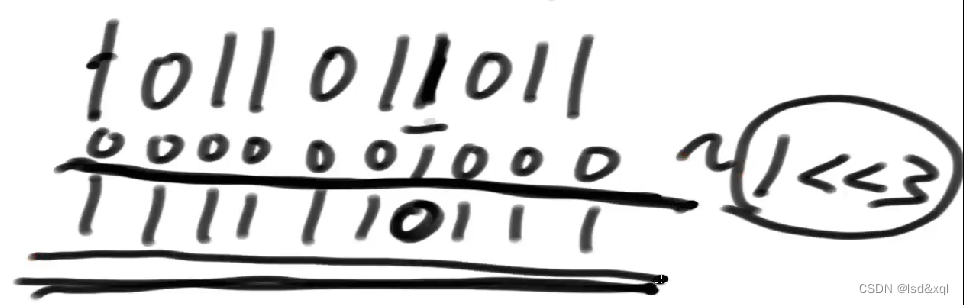
public void delete(int num) {
bit[num>>6] &= ~(1L <<(num&63));
}

3、位图里面查询元素
就可以直接找到那一位并做一个与运算则完成了
public boolean contains(int num) {
return bits[num>>6] &(1L<<(num&63)) != 0
}

整体整合代码如下：

public static class BitMap {

		private long[] bits;

		public BitMap(int max) {
			bits = new long[(max + 64) >> 6];
		}

		public void add(int num) {
			bits[num >> 6] |= (1L << (num & 63));
		}

		public void delete(int num) {
			bits[num >> 6] &= ~(1L << (num & 63));
		}

		public boolean contains(int num) {
			return (bits[num >> 6] & (1L << (num & 63))) != 0;
		}

	}

	public static void main(String[] args) {
		System.out.println("测试开始！");
		int max = 10000;
		BitMap bitMap = new BitMap(max);
		HashSet<Integer> set = new HashSet<>();
		int testTime = 10000000;
		for (int i = 0; i < testTime; i++) {
			int num = (int) (Math.random() * (max + 1));
			double decide = Math.random();
			if (decide < 0.333) {
				bitMap.add(num);
				set.add(num);
			} else if (decide < 0.666) {
				bitMap.delete(num);
				set.remove(num);
			} else {
				if (bitMap.contains(num) != set.contains(num)) {
					System.out.println("Oops!");
					break;
				}
			}
		}
		for (int num = 0; num <= max; num++) {
			if (bitMap.contains(num) != set.contains(num)) {
				System.out.println("Oops!");
			}
		}
		System.out.println("测试结束！");
	}

位运算实现 + - * /

加法

如下例子：46+20 可拆分为以下两步：

1、首先要知道异或是无进位相加的结果，（相同为0不同为1）
如 0101110^ 0010100 = 0111010

2、a&b 之后再往左移则为 a+b的进位信息
0101110&0010100 = 0000100 <<1
0001000
这里我们就可以根据异或的结果和a&b左移的结果不断的往下推
，直到进位信息为0以后则最终的值就是加后的值
代码实现如下：

	public static int add(int a, int b) {
		int sum = a;
		//直到进位信息变成0则最终返回的是无进位相加信息
		while (b != 0) {
			sum = a ^ b;//无进位相加的信息->sum
			b = (a & b) << 1;//进位信息 -> b->b'
			a = sum;// a->a'
		}
		return sum;
	}

减法

a-b 则为 a+b的相反数
b的相反数则为~b+1,但是不能出现加号
则可以这样来用如上的add方法
add(a,add(~b,1))

	public static int negNum(int n) {
		return add(~n, 1);
	}

	public static int minus(int a, int b) {
		return add(a, negNum(b));
	}

乘法

和小学的竖式乘法相同

以 a:0110
b:0111为例子
a*b
除了第一位的一，其他位置的一结果都向后补0
ans = 0110+ 01100+011000
代码如下：

public static int multi(int a, int b) {
		int res = 0;
		while (b != 0) {
			if ((b & 1) != 0) {
				res = add(res, a);
			}
			a <<= 1;
			b >>>= 1;//无符号右移（如果带符号的话那么这个代码就跑不完了）
		}
		return res;
	}

除法

首先
a/b = c
这里b 为 00110
然后c为 01100
那么a = bc= b2的二次方+b*2的三次方
那么怎么去求得这个c呢
让a减掉尽可能大的2的某次方乘以b
减完之后剩下一个a1然后再减去一个尽可能大的2的某次方乘以b
得到a2，然后再让a2继续减
直到减到an的值为0，那么就可以得到除法的结果
因为每次的二的某次方都代表最终的结果的第某次方位上为1
代码如下：
leetcode题 https://leetcode.com/problems/divide-two-integers

public static int add(int a, int b) {
		int sum = a;
		//直到进位信息变成0则最终返回的是无进位相加信息
		while (b != 0) {
			sum = a ^ b;//无进位相加的信息->sum
			b = (a & b) << 1;//进位信息 -> b->b'
			a = sum;// a->a'
		}
		return sum;
	}

	public static int negNum(int n) {
		return add(~n, 1);
	}

	public static int minus(int a, int b) {
		return add(a, negNum(b));
	}

	public static int multi(int a, int b) {
		int res = 0;
		while (b != 0) {
			if ((b & 1) != 0) {
				res = add(res, a);
			}
			a <<= 1;
			b >>>= 1;
		}
		return res;
	}

	public static boolean isNeg(int n) {
		return n < 0;
	}

	public static int div(int a, int b) {
		int x = isNeg(a) ? negNum(a) : a;
		int y = isNeg(b) ? negNum(b) : b;
		int res = 0;
		//x/y 让x去够着y，如果让y去够着x的话y需要左移可能需要移动到最左端
		//，如果到符号位上去了，那这个数就可能变成负数了，我就没法探知到这个数了，而让x右移则不会出现改符号位的情况
		//x取30不包含符号位（因为这里已经对负数取反了）
		for (int i = 30; i >= 0; i = minus(i, 1)) {
			if ((x >> i) >= y) {
				res |= (1 << i);
				x = minus(x, y << i);
			}
		}
		//异或判断符号是否相同，不同则取反，相同则结果就是res
		return isNeg(a) ^ isNeg(b) ? negNum(res) : res;
	}

//如下考虑系统最小值无法转绝对值
	public static int divide(int a, int b) {
		if (a == Integer.MIN_VALUE && b == Integer.MIN_VALUE) {
			return 1;
		} else if (b == Integer.MIN_VALUE) {
			return 0;
		} else if (a == Integer.MIN_VALUE) {
			if (b == negNum(1)) {
				return Integer.MAX_VALUE;
			} else {
				//a/b
				//(a+1)/b = c
				//a - (b*c) = d
				//d /b =e
				//ans = c+e
				int c = div(add(a, 1), b);
				return add(c, div(minus(a, multi(c, b)), b));
			}
		} else {
			return div(a, b);
		}
	}

如上代码假设-15系统最小，我们要求
-15/3的结果
我们可以先用 -14/3 = -4
然后通过-4*3 我们得到的是-12
然而-15 和-12差的是-3
然后再用这个补偿值去除以3
-3/3 = -1
用如上的-4±1 = -5得到最后的结果
这样就绕过了-15无法转换位15的情况