28、损失函数（多分类交叉熵损失）

原创已于 2025-11-26 17:19:16 修改 · 562 阅读

11 ·

CC 4.0 BY-SA版权

文章标签：

#python #深度学习 #pytorch

于 2025-11-26 16:10:11 首次发布

深度学习专栏收录该内容

44 篇文章

订阅专栏

部署运行你感兴趣的模型镜像

学习目标

分类任务的损失函数
回归任务的损失函数

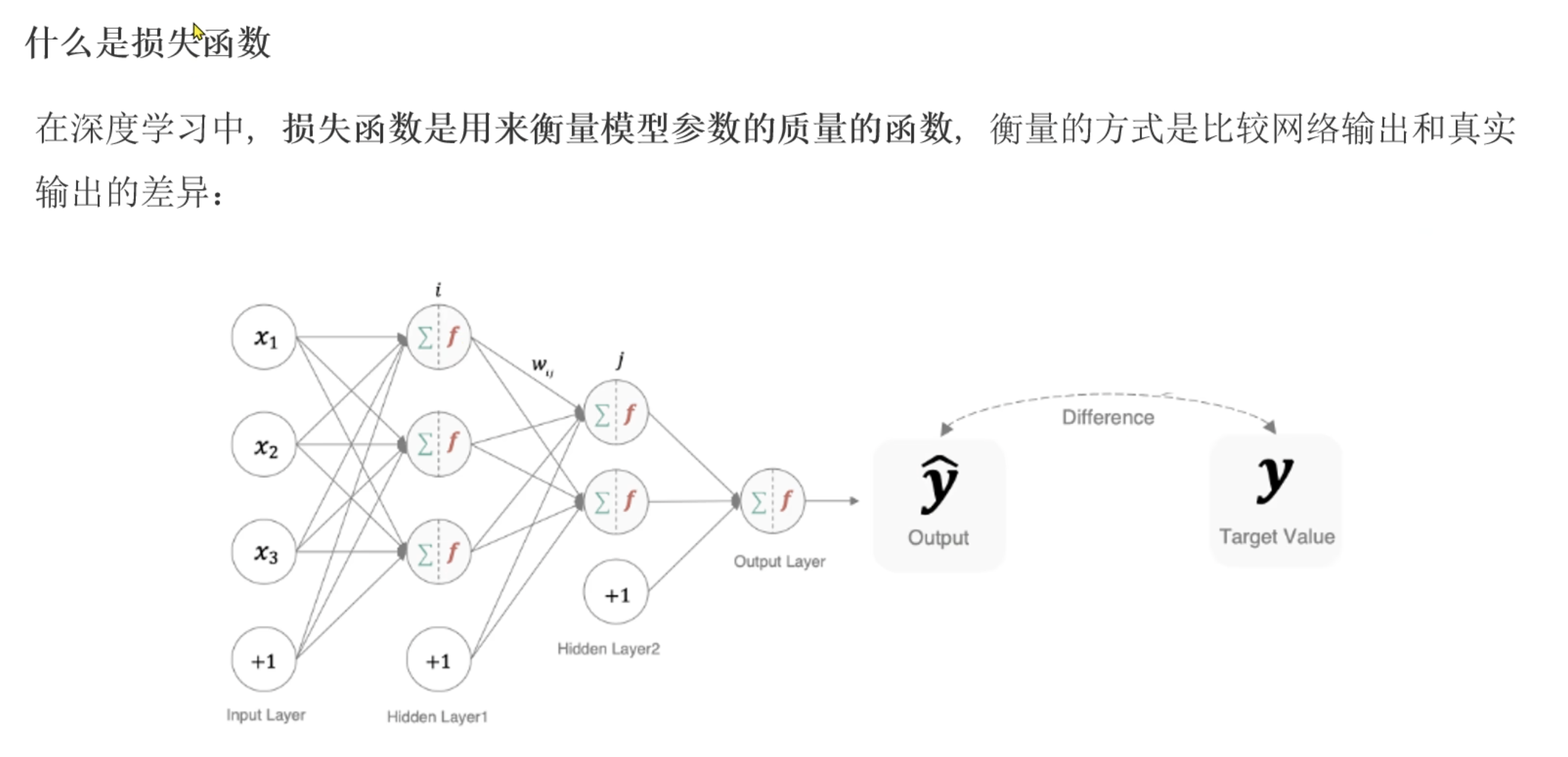
什么是损失函数

损失函数是用于衡量模型参数质量的函数，衡量方式就是比较预测值和真实值的差异
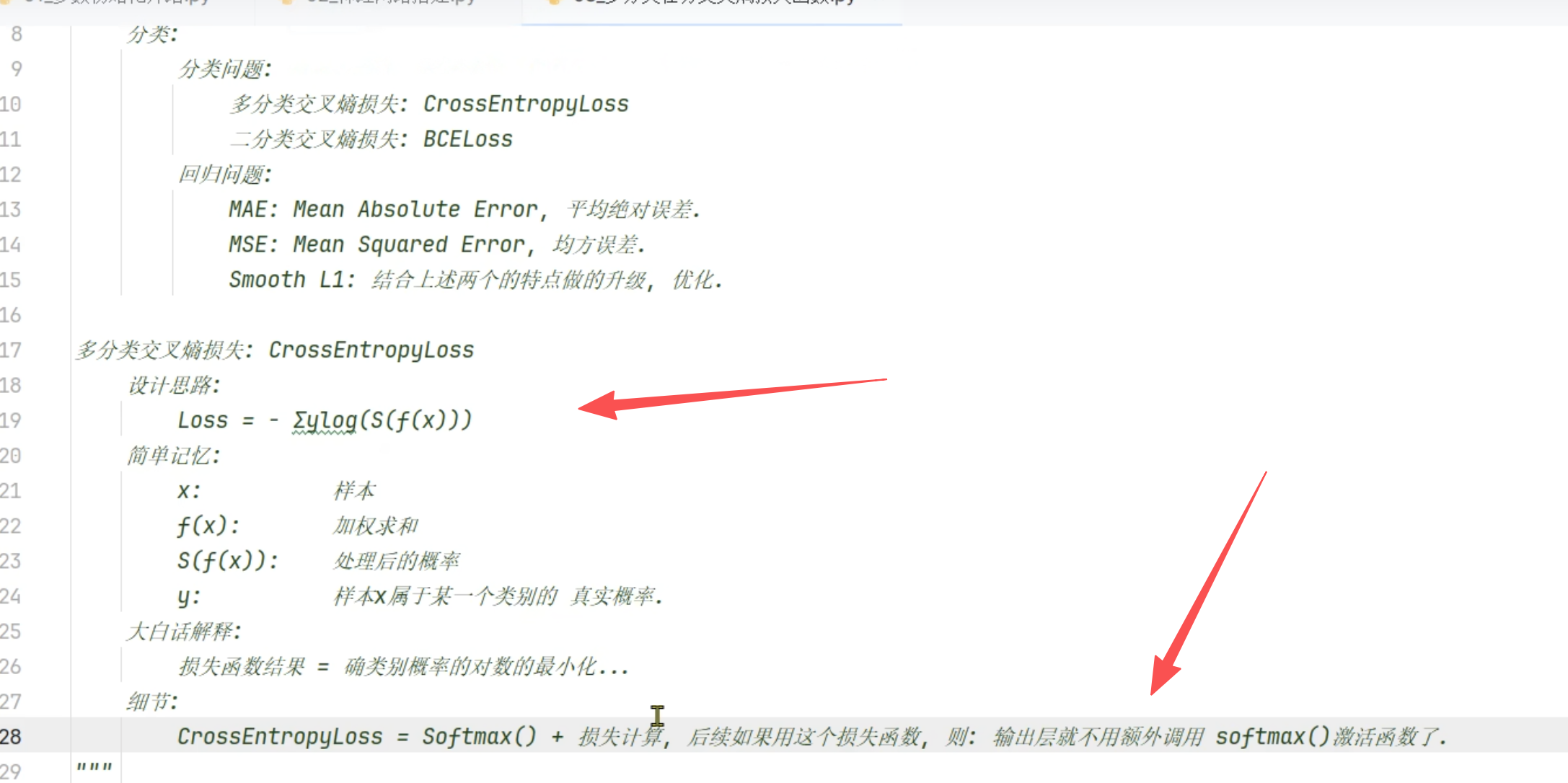
因为多分类交叉熵损失的公式中，包含softmax，则我们在输出层多分类的问题，在使用多分类交叉熵的情况下，输出层可以不使用softmax激活函数
x为输入特征
f（x）为加权求和，对x进行加权求和，为预测值z
s就是softmax，也就是激活函数。 S（f（x））结果也是一个概率，所有概率和为1。为激活函数后的值
y是对于x是否属于一个类别的真实概率，也就是要么属于要么不属于，只有0和1 两种情况，真实值

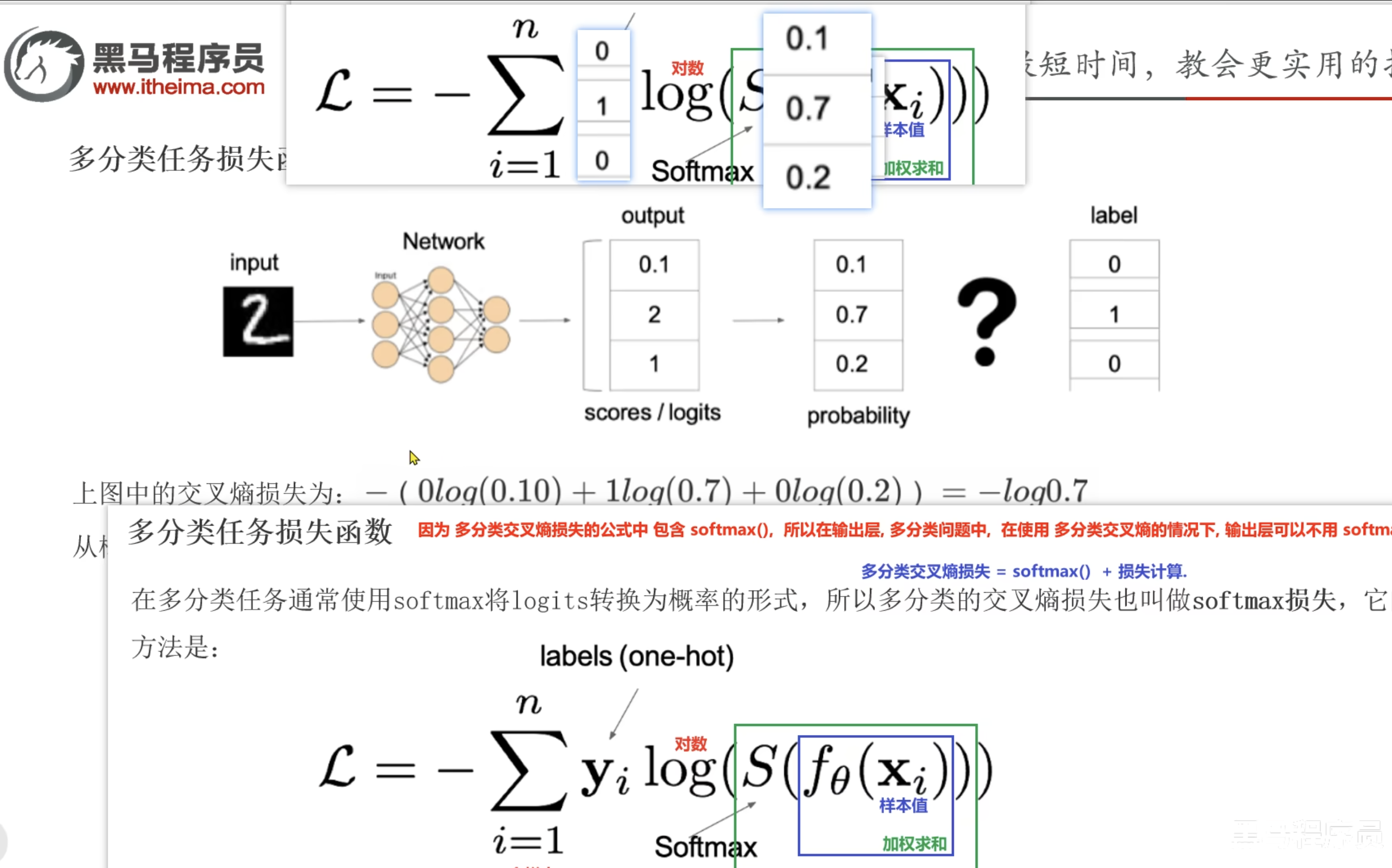
案例

0.1，2，1 就是我们的加权求和的数据
0.1, 0.7, 0.2 就是其中上面预测值经过softmax激活函数的预测值。图片上的这里是应该预测之后的值了
0，1， 0就是我们的y，到底是不是属于这一个类别
我们需要最小化正确类别所对应概率的对数的负值

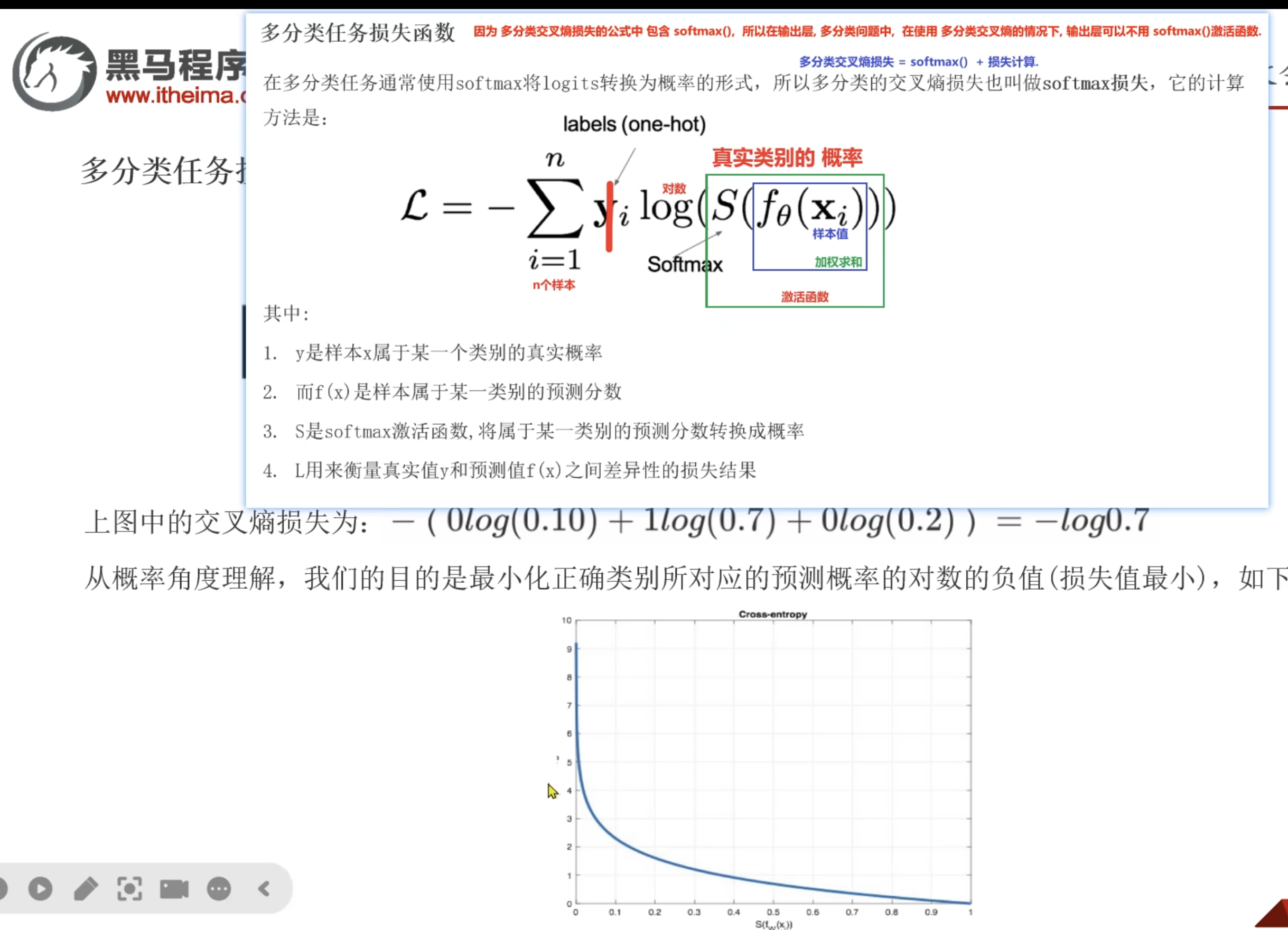
最小化正确类别所对应概率的对数的负值

正确类别：因为我们的y，只会是0或者1，则0不会存在，所以就只有1，1就是真实类别，预测对了
正确类别的概概率：就是对x的加权求和后的softmax激活函数后的一个概率。那么就是s（f（x））
所以就是最小话正确类别的概率的对数的负值

是加权求和后是预测值，还是加权求和后的值经过激活函数才是预测值？

两种情况都存在，取决于你使用的模型。

1. 加权求和后直接是预测值

这种情况对应的是线性模型，没有使用激活函数。

2. 加权求和后的值经过激活函数才是预测值

这种情况对应的是非线性模型，或者需要特定输出范围的模型。激活函数引入了非线性，使得模型可以学习更复杂的数据模式。

真实概率的one-hot编码以及简易模式

这里的"真实概率"实际上是one-hot编码：

# 对于3分类问题，如果有3个样本：
y_true = [
    [1, 0, 0],  # 样本1属于类别0的"真实概率"：100%
    [0, 1, 0],  # 样本2属于类别1的"真实概率"：100%  
    [0, 0, 1]   # 样本3属于类别2的"真实概率"：100%
]

# 对应的类别索引表示：
y_true_indices = [0, 1, 2]

实际使用中的简化

理论公式 vs 实际实现：

理论公式：

y_i 是one-hot向量：[1, 0, 0], [0, 1, 0]等
每个位置都是0或1，表示"真实概率"

实际实现（如PyTorch的CrossEntropyLoss）：

使用类别索引：[0, 1, 2]
损失函数内部会自动转换为one-hot形式

为什么会有这种差异？

数学上的完整性：

公式需要完整描述概率分布
从数学角度，应该写成完整的分布形式

工程上的效率：

存储[0, 1, 2]比存储one-hot矩阵更节省内存
计算时内部转换更高效

举例说明

import torch
import torch.nn as nn

def compare_formats():
    # 3个样本，3个类别
    y_true_indices = torch.tensor([0, 2, 1])  # 实际使用的格式
    
    # 对应的one-hot格式（理论公式中的y_i）
    y_true_onehot = torch.tensor([
        [1., 0., 0.],
        [0., 0., 1.], 
        [0., 1., 0.]
    ])
    
    # 预测logits
    logits = torch.tensor([
        [2.0, 0.5, -1.0],
        [0.1, 1.0, 3.0],
        [-1.0, 2.0, 0.5]
    ])
    
    # 方法1：使用索引格式（实际常用）
    criterion1 = nn.CrossEntropyLoss()
    loss1 = criterion1(logits, y_true_indices)
    
    # 方法2：手动实现理论公式
    softmax = nn.Softmax(dim=1)
    probs = softmax(logits)
    loss2 = -(y_true_onehot * torch.log(probs)).sum(dim=1).mean()
    
    print(f"索引格式损失: {loss1:.4f}")
    print(f"One-hot格式损失: {loss2:.4f}")
    print("两种方法结果相同:", torch.isclose(loss1, loss2))

compare_formats()

总结

您完全正确！在多分类中：

理论公式中的y_i确实是one-hot向量，每个位置是0或1的"真实概率"
实际代码中通常使用类别索引[0, 1, 2]来简化表示
两种表示在数学上是等价的，只是实现方式的差异

多分类和二分类的区别！！！！

都是one-hot编码格式的话：多分类是[[]] 两个【】，二分类是[] 一个【】
多分类的简易模式：可能会出现非01的例如[1, 0, 2]
也就是多分类，1的位置索引可能在3个不同的位置
这是多分类的one-hot表示（2个样本，3个类别）,一个样本有三个位置(1可能会出现3个位置)，就会出3个类别 y_true = torch.tensor([[0, 1, 0], [1, 0, 0]], dtype=torch.float)

例子分析：

# 例子1：这是多分类的one-hot表示（2个样本，3个类别）
y_true = torch.tensor([[0, 1, 0], [1, 0, 0]], dtype=torch.float)
# 第一个样本：类别1（索引1处为1）
# 第二个样本：类别0（索引0处为1）
# 这是3分类问题（因为有3个位置）

# 例子2：这是二分类的类别索引表示
y_true = torch.tensor([1, 0], dtype=torch.float)
# 第一个样本：类别1
# 第二个样本：类别0
# 这是2分类问题（只有0和1两个值）

# 例子3：这是二分类的类别索引表示
y_true = torch.tensor([0, 1, 0], dtype=torch.float)
# 三个样本分别属于类别0、1、0
# 这是2分类问题（只有0和1两个值）

关键区别总结

二分类的标签表示：

# 方式1：类别索引（最常用）
y_true = torch.tensor([0, 1, 0, 1])  # 每个样本一个0或1

# 方式2：one-hot编码（较少用）
y_true = torch.tensor([[1, 0], [0, 1], [1, 0], [0, 1]])

多分类的标签表示：

# 方式1：类别索引（最常用）
y_true = torch.tensor([0, 2, 1, 0])  # 每个样本一个整数（0到K-1）

# 方式2：one-hot编码
y_true = torch.tensor([
    [1, 0, 0],  # 类别0
    [0, 0, 1],  # 类别2
    [0, 1, 0],  # 类别1
    [1, 0, 0]   # 类别0
])

判断分类数量的方法

从类别索引判断：

# 二分类：值只能是0或1
y_true = torch.tensor([0, 1, 0, 1])  # 2分类

# 多分类：值可以是0,1,2,...K-1
y_true = torch.tensor([0, 2, 1, 0])  # 至少3分类（因为有0,1,2）

从one-hot编码判断：

# 二分类：每个向量长度=2
y_true = torch.tensor([[1,0], [0,1], [1,0]])  # 2分类

# 多分类：每个向量长度=K（K>2）
y_true = torch.tensor([[1,0,0], [0,0,1], [0,1,0]])  # 3分类

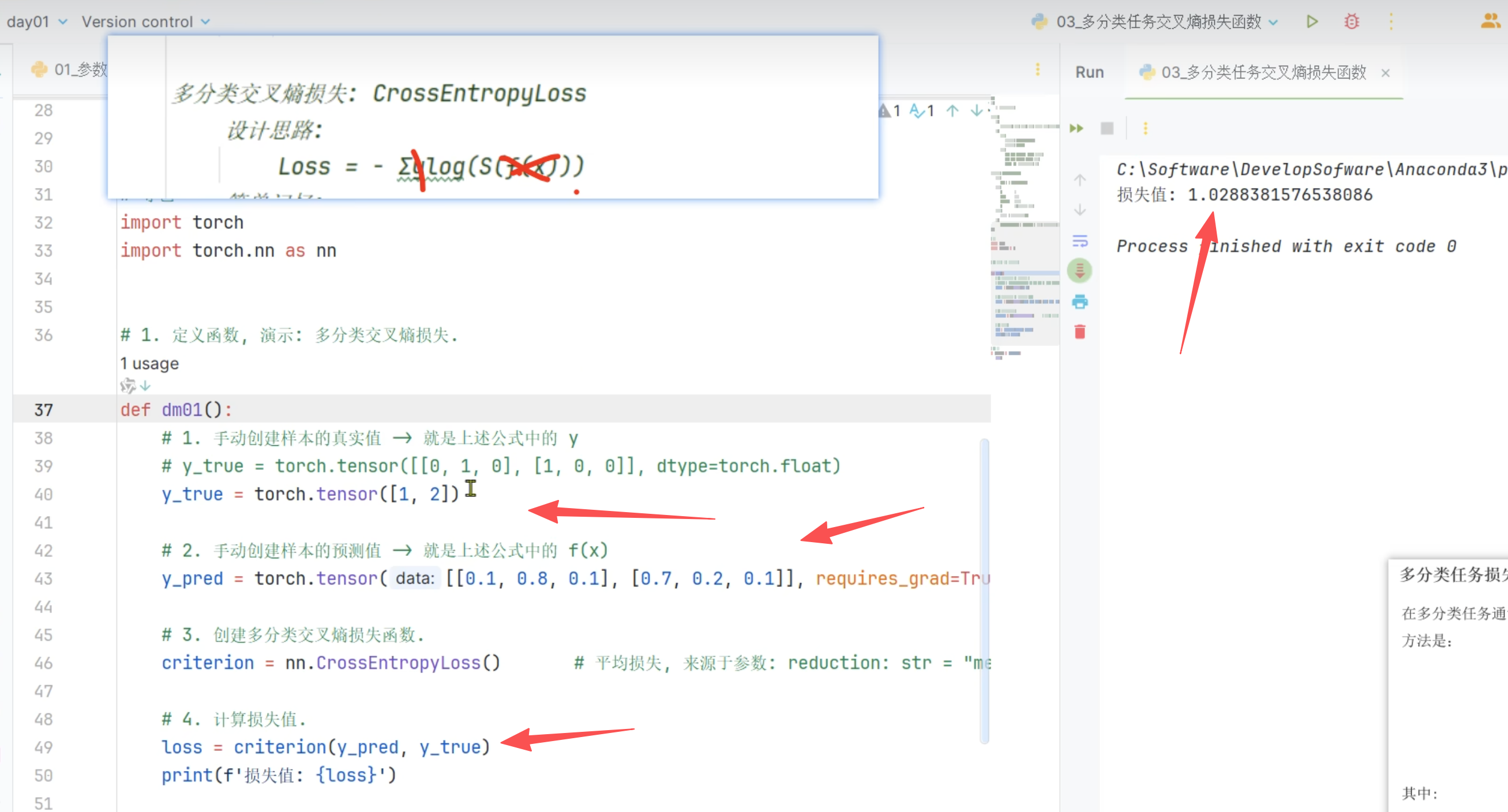
测试代码

CrossEntropyLoss是个平均损失函数
创建预测值（肯定是概率了），这个相当于f(x)了，还需要softmax处理，在CrossEntropyLoss中
真实类别1的概率 = e^0.8 / (e^0.1*2 + e^0.8) ≈ 2.226/4.436 ≈ 0.5017
损失 = -log(0.5017) ≈ 0.691
真实类别0的概率 = e^0.7 / (e^0.7+e^0.2+e^0.1) ≈ 2.014/4.34 ≈ 0.464
损失 = -log(0.464) ≈ 0.768
最终损失 = (0.691 + 0.768)/2 ≈ 0.7295

import torch
import torch.nn as nn

def demo1():
    # 创建真实值，只能有0，1，但是表示的可能是3个类，A，B，C  表示的是不是A，C而是B。这里的[0, 1, 0]是一个整体
    y_true = torch.tensor([[0, 1, 0]], dtype=torch.float)


    # 创建预测值（肯定是概率了），这个相当于f(x)了，还需要softmax处理，在CrossEntropyLoss中
    y_pred = torch.tensor([[0.1, 2, 1]], dtype=torch.float)

    # 定义损失函数 会对输入进行 softmax
    criterion = nn.CrossEntropyLoss()


    # 真实类别1的概率 = e^2 / (e^0.1 + e^2 + e^1) ≈ 7.389 / (1.105 + 7.389 + 2.718) ≈ 7.389/11.212 ≈ 0.659
    # 损失 = -log(0.659) ≈ 0.417
    loss = criterion(y_pred, y_true)

    print(loss)

def demo2():
    # 创建真实值，只能有0，1
    # one-hot向量
    # 实际代码中通常使用类别索引[0, 1, 2]来简化表示，这里就是两组值，外面有两层[[]]
    '''
     例子1：这是多分类的one-hot表示（2个样本，3个类别）,一个样本有三个位置(1可能会出现3个位置)，就会出3个类别
        y_true = torch.tensor([[0, 1, 0], [1, 0, 0]], dtype=torch.float)
        第一个样本：类别1（索引1处为1）
        第二个样本：类别0（索引0处为1）
        这是3分类问题（因为有3个位置）
        
    例子2：这是二分类的类别索引表示
        y_true = torch.tensor([1, 0], dtype=torch.float)
        第一个样本：类别1
        第二个样本：类别0
        这是2分类问题（只有0和1两个值）
    
    例子3：这是二分类的类别索引表示
        y_true = torch.tensor([0, 1, 0], dtype=torch.float)
        三个样本分别属于类别0、1、0
        这是2分类问题（只有0和1两个值）
    '''
    # y_true = torch.tensor([[0, 1, 0], [1, 0, 0]], dtype=torch.float)，
    # 就是1所在的索引，第一组1索引在1， 第二组1索引在0。1的索引有多少不同的分类就有多少分类
    y_true = torch.tensor([1, 0], dtype=torch.float)


    # 创建预测值（肯定是概率了），这个相当于f(x)了，还需要softmax处理，在CrossEntropyLoss中。不需要和为1概率随便写就行
    y_pred = torch.tensor([[0.1, 0.8, 0.1], [0.7, 0.2, 0.1]], dtype=torch.float)

    # 定义损失函数 会对输入进行 softmax
    criterion = nn.CrossEntropyLoss()

    # 真实类别1的概率 = e^0.8 / (e^0.1*2 + e^0.8) ≈ 2.226/4.436 ≈ 0.5017
    # 损失 = -log(0.5017) ≈ 0.691

    # 真实类别0的概率 = e^0.7 / (e^0.7+e^0.2+e^0.1) ≈ 2.014/4.34 ≈ 0.464
    # 损失 = -log(0.464) ≈ 0.768

    # 最终损失 = (0.691 + 0.768)/2 ≈ 0.7295
    loss = criterion(y_pred, y_true)

    print(loss)

if __name__ == '__main__':
    demo1()
    demo2()

测试结果

D:\software\python.exe -X pycache_prefix=C:\Users\HONOR\AppData\Local\JetBrains\PyCharm2025.2\cpython-cache "D:/software/PyCharm 2025.2.4/plugins/python-ce/helpers/pydev/pydevd.py" --multiprocess --qt-support=auto --client 127.0.0.1 --port 49894 --file C:\Users\HONOR\Desktop\python\test20_loss.py 
Connected to: <socket.socket fd=884, family=2, type=1, proto=0, laddr=('127.0.0.1', 49895), raddr=('127.0.0.1', 49894)>.
Connected to pydev debugger (build 252.27397.106)
tensor(0.4170)
tensor(0.7288)

Process finished with exit code 0