24、模拟线性回归

最新推荐文章于 2025-12-22 18:37:45 发布

原创最新推荐文章于 2025-12-22 18:37:45 发布 · 824 阅读

10 ·

CC 4.0 BY-SA版权

文章标签：

#深度学习 #pytorch #python #线性回归

深度学习专栏收录该内容

44 篇文章

订阅专栏

部署运行你感兴趣的模型镜像

模拟线性回归步骤

创造模拟数据，输入特征，权重w，真实值y
np - > 张量 -> 数据集-> 数据加载器
dataset 使用张量创建数据集（监督学习）：需要两个参数，一个输入值x ，一个目标值y
dataloader 使用数据加载器，定义好每个批次中的数量，是否打乱等
model 创建线性回归模型 ,定义好输入和输出维度nn.Linear(1, 1)
criterion 创建损失函数 nn.MSELoss()
optimizer 创建优化器，定义好学习率 optimizer = optim.SGD(model.parameters(),lr=1e-2)
每轮（epochs），每批（是针对数据加载器的）进行训练（for train_x, train_y in dataloader:）
y_pred 模型计算预测值 y_pred = model(train_x)
loss 损失函数计算损失值，需要使用z也就是y_pred ，注意是z对y，预测值对真实值预测值是第一个参数，和真实值loss = criterion(y_pred, train_y.reshape(-1,1))
使用优化器，进行梯度清零 optimizer.zero_grad()
对loss进行反向传播 loss.backward()
最后一步：梯度更新，也是优化器来做 optimizer.step()

总体训练步骤 10步操作

训练前的准备工作(5步)
开始训练的（5步）

训练前的准备工作(5步)

1.使用，x 输入值和真实值y 创建数据集 dataset
2.创建并配置数据加载器，定义好批次和是否打乱顺序 dataloader
3.定义模型（这里是一个简单线性模型） model
4.定义损失函数 criterion
5.创建优化器，并定义高学习率 optimizer

开始训练的（5步）

1.使用模型计算预测值 y_pred = model(batch_x)
2.使用损失函数计算损失值 loss = criterion(y_pred, batch_y)
3.优化器进行梯度清零 optimizer.zero_grad()
4.对损失值进行反向传播 loss.backward()
5. 优化器进行梯度更新 optimizer.step()

def train_model(x, y, coef):
    # 1.使用，x 输入值和真实值y 创建数据集
    dataset = TensorDataset(x,y)
    # 2.创建并配置数据加载器，定义好批次和是否打乱顺序
    dataloader = DataLoader(dataset,batch_size=16, shuffle=True)
    # 3.定义模型（这里是一个简单线性模型）
    model = nn.Linear(1,1)
    # 4.定义损失函数
    criterion = nn.MSELoss
    # 5.创建优化器，并定义高学习率
    optimizer = optim.SGD(model.parameters(), lr=0.01)

    # 开始训练
    # 6.定义好训练轮数
    epochs = 100
    # 7.开始每轮每批开始训练
    for epoch in range(epochs):
        for batch_x,batch_y in dataloader:
            # 1.使用模型计算预测值
            y_pred = model(batch_x)
            # 2.使用损失函数计算损失值
            loss = criterion(y_pred, batch_y)
            # 3.优化器进行梯度清零
            optimizer.zero_grad()
            # 4.对损失值进行反向传播
            loss.backward()
            # 5. 优化器进行梯度更新
            optimizer.step()

创建线性模拟数据

make_regression
返回 x, y, coef
x为输入特征
y是真实数据
coef 是w, 设置为True表示返回真实系数，coef=True 主要就是让你知道真实的权重 w。
bias 为偏置b

# x为输入特征
    # y是真实数据
    # coef 是w, 为true表示自动初始化出来
    x, y, coef = make_regression(
        n_samples=100,
        n_features=1,
        noise=10,
        coef=True,
        bias= 14.5,
        random_state=3)

def create_dataset():
    # x为输入特征
    # y是真实数据
    # coef 是w, 设置为True表示返回真实系数，coef=True 主要就是让你知道真实的权重 w。
    x, y, coef = make_regression(
        n_samples=100,
        n_features=1,
        noise=10,
        coef=True, # 设置为True表示返回真实系数
        bias= 14.5,
        random_state=3)

    print(type(x), type(y))
    # x (100, 1)  是 二维数组  [[x₁],[x₂], [x₃], ... [x₁₀₀]]
    print(x.shape, y.shape)

    x = torch.tensor(x,dtype=torch.float)
    y = torch.tensor(y,dtype=torch.float)

    return x,y,coef

数据集(DataSet)的作用：

数据集是数据的容器和访问接口，它负责：

存储所有数据
提供统一的数据访问方式
实现数据预处理和转换

监督学习的基本结构

在监督学习中，我们总是有：

x: 输入特征 (features)
y: 目标标签 (labels)

import torch
from torch.utils.data import TensorDataset

# 示例：房价预测
x = torch.tensor([[100, 2], [150, 3], [200, 4]], dtype=torch.float32)  # [面积, 卧室数]
y = torch.tensor([300, 450, 600], dtype=torch.float32)  # 房价

dataset = TensorDataset(x, y)

数据集加载器(DataLoader)

负责给数据集分批，还有打乱
DataLoader（）
从数据集中按批次抽取数据
打乱数据顺序
多进程数据加载
真正实现分批
数据加载器返回的是 (x_batch, y_batch)

    # 2. 创建数据集加载器
    # 参数分别为 数据集， 每批多少数据， 是否打乱
    dataloader = DataLoader(dataset,batch_size=16,shuffle=True)

定义模型nn.Linear

nn.Linear 实际上是一个全连接层（Fully Connected Layer）

# 示例1: 1维输入 → 1维输出 (简单线性回归)
model1 = nn.Linear(1, 1)  # y = w*x + b

# 示例2: 1维输入 → 3维输出 (特征变换)
model2 = nn.Linear(1, 3)  # 输出3个值: [y1, y2, y3] = [w1*x+b1, w2*x+b2, w3*x+b3]

# 示例3: 3维输入 → 1维输出 (多特征回归)
model3 = nn.Linear(3, 1)  # y = w1*x1 + w2*x2 + w3*x3 + b

# 示例4: 3维输入 → 2维输出 (降维或多元输出)
model4 = nn.Linear(3, 2)  # 输出2个值: [y1, y2]

使用损失函数计算损失值

loss = criterion(y_pred, train_y.reshape(-1,1))
使用损失函数计算损失值（-1,1）表示-1所有行，1都转为1列的数据，例如就算是23，转换后都是61这样的

# 各种 reshape 示例
data = torch.tensor([1, 2, 3, 4, 5, 6])

print("原始数据:", data.shape)
print("reshape(-1, 1):", data.reshape(-1, 1).shape)    # (6, 1)
print("reshape(2, -1):", data.reshape(2, -1).shape)    # (2, 3) 
print("reshape(3, -1):", data.reshape(3, -1).shape)    # (3, 2)
print("reshape(-1, 2):", data.reshape(-1, 2).shape)    # (3, 2)
print("reshape(1, -1):", data.reshape(1, -1).shape)    # (1, 6)

loss 的本质：

不是简单数字：是包含完整计算历史的特殊Tensor
计算图的终点：记录了从数据到预测到损失的所有运算
梯度计算的起点：反向传播从这里开始，沿着计算图回溯

测试代码

import torch
import torchvision
from torch.utils.data import TensorDataset, DataLoader
from torch import nn
from torch import optim
from sklearn.datasets import make_regression
import matplotlib.pyplot as plt

plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False


def create_dataset():
    # x为输入特征
    # y是真实数据
    # coef 是w, 设置为True表示返回真实系数，coef=True 主要就是让你知道真实的权重 w。
    x, y, coef = make_regression(
        n_samples=100,
        n_features=1,
        noise=10,
        coef=True, # 设置为True表示返回真实系数
        bias= 14.5,
        random_state=3)

    print(type(x), type(y))
    # x (100, 1)  是 二维数组  [[x₁],[x₂], [x₃], ... [x₁₀₀]]
    print(x.shape, y.shape)

    x = torch.tensor(x,dtype=torch.float)
    y = torch.tensor(y,dtype=torch.float)

    return x,y,coef

def train_model(x, y, coef):
    # 1. 创建数据集： tensor -> 数据集对象
    # 在监督学习中，我们总是有：
    # x: 输入特征(features)
    # y: 目标标签(labels)
    dataset = TensorDataset(x,y)

    # 2. 创建数据集加载器
    # 参数分别为 数据集， 每批多少数据， 是否打乱
    dataloader = DataLoader(dataset,batch_size=16,shuffle=True)

    # 3. 创建初始的线性回归模型（创建模型结构（空壳））
    model = nn.Linear(1, 1) # 1维输入 → 1维输出 (简单线性回归)

    # 4. 创建损失函数
    criterion = nn.MSELoss()

    # 5. 创建优化器，lr 为学习率，1e-2 表示10的-2次方，0.01
    optimizer = optim.SGD(model.parameters(),lr=1e-2)

    epochs, loss_list, total_loss, total_sample = 100, [], 0.0, 0

    # 100轮（0到99）
    for epoch in range(epochs):
        # 分别数输入特征，  和 真实值y
        for train_x, train_y in dataloader:
            # 预测值
            y_pred = model(train_x)
            # 使用损失函数计算损失值（-1,1）-1表示所有行，转换为1列的数据
            loss = criterion(y_pred, train_y.reshape(-1,1))
            # 每批的总损失
            total_loss += loss.item()
            # 多少批
            total_sample += 1

            # 梯度清理
            optimizer.zero_grad()
            # 对损失值进行 反向传播
            loss.backward()
            # 梯度更新
            optimizer.step()

        # 每轮的平均损失，记录（100轮）
        loss_list.append(total_loss/total_sample)
        print(f'轮数: {epoch + 1}, 平均损失值: {total_loss/total_sample}')


    print(f'{epochs} 轮的平均损失分别为:{loss_list}' )
    # 训练后，我们的模型更新后的w 和 b  原始值是27.478050549563925， 和 14.5，训练100轮后的为27.7562 和 14.0686
    print(f'模型的权重：{model.weight}, \n模型的偏置：{model.bias}')

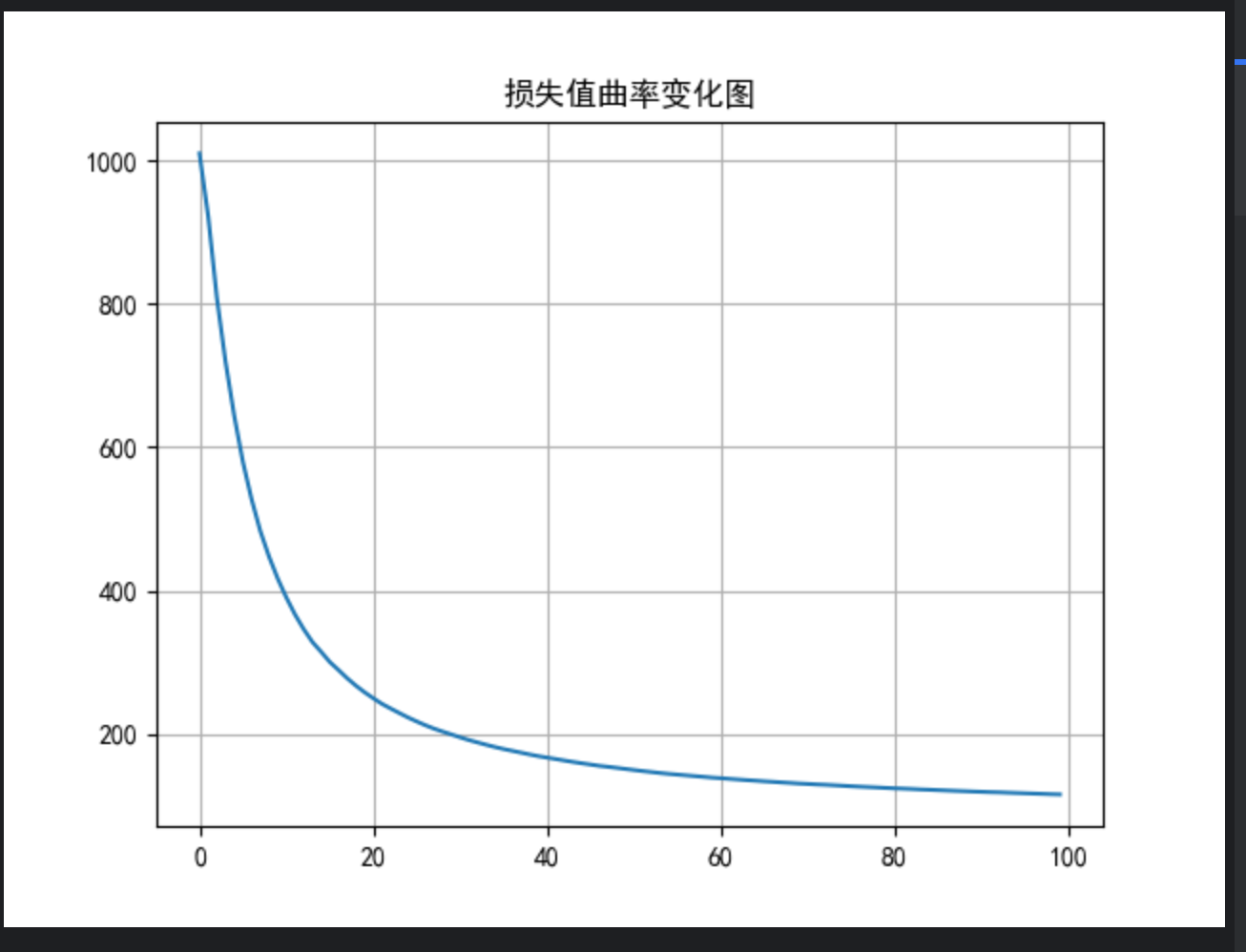
    # 绘制损失曲线
    plt.plot(range(epochs), loss_list)
    plt.title('损失值曲率变化图')
    plt.grid()
    plt.show()

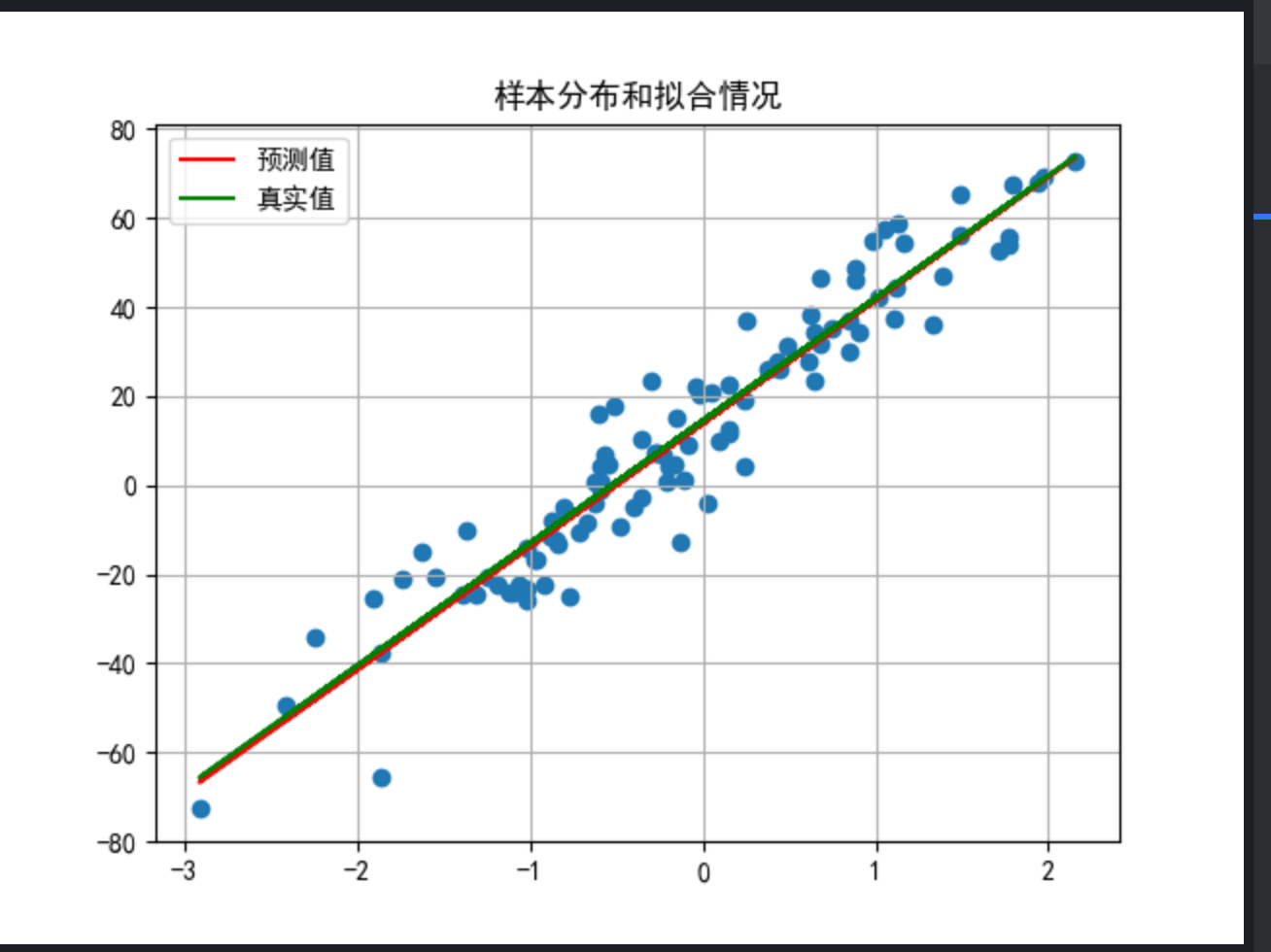
    # 绘制样本点分布情况
    plt.scatter(x,y)
    plt.title('样本分布和拟合情况')
    # 预测值
    y_pred = x * model.weight + model.bias
    # 真实值
    y_true = x * coef.item() + 14.5

    plt.plot(x, y_pred.detach().numpy(), color='red', label='预测值')
    plt.plot(x, y_true.detach().numpy(), color='green', label='真实值')
    # 图例，网格。
    plt.legend()
    plt.grid()
    plt.show()


# def train_model(x, y, coef):
#     # 1.使用，x 输入值和真实值y 创建数据集
#     dataset = TensorDataset(x,y)
#     # 2.创建并配置数据加载器，定义好批次和是否打乱顺序
#     dataloader = DataLoader(dataset,batch_size=16, shuffle=True)
#     # 3.定义模型（这里是一个简单线性模型）
#     model = nn.Linear(1,1)
#     # 4.定义损失函数
#     criterion = nn.MSELoss
#     # 5.创建优化器，并定义高学习率
#     optimizer = optim.SGD(model.parameters(), lr=0.01)
#
#     # 开始训练
#     # 6.定义好训练轮数
#     epochs = 100
#     # 7.开始每轮每批开始训练
#     for epoch in range(epochs):
#         for batch_x,batch_y in dataloader:
#             # 1.使用模型计算预测值
#             y_pred = model(batch_x)
#             # 2.使用损失函数计算损失值
#             loss = criterion(y_pred, batch_y)
#             # 3.优化器进行梯度清零
#             optimizer.zero_grad()
#             # 4.对损失值进行反向传播
#             loss.backward()
#             # 5. 优化器进行梯度更新
#             optimizer.step()










if __name__ == '__main__':
    create_dataset()
    x,y,coef = create_dataset()
    print(f'x: \n{x}, \n y: \n{y}, \n coef: \n{coef}')
    train_model(x,y,coef)

测试结果

D:\software\python.exe -X pycache_prefix=C:\Users\HONOR\AppData\Local\JetBrains\PyCharm2025.2\cpython-cache "D:/software/PyCharm 2025.2.4/plugins/python-ce/helpers/pydev/pydevd.py" --multiprocess --qt-support=auto --client 127.0.0.1 --port 61094 --file C:\Users\HONOR\Desktop\python\test16.py 
Connected to: <socket.socket fd=968, family=2, type=1, proto=0, laddr=('127.0.0.1', 61095), raddr=('127.0.0.1', 61094)>.
Connected to pydev debugger (build 252.27397.106)
<class 'numpy.ndarray'> <class 'numpy.ndarray'>
(100, 1) (100,)
<class 'numpy.ndarray'> <class 'numpy.ndarray'>
(100, 1) (100,)
x: 
tensor([[ 0.1506],
        [-0.8887],
        [-1.8609],
        [ 0.1529],
        [ 0.8993],
        [-0.8038],
        [ 1.7746],
        [ 0.6467],
        [-1.7431],
        [-0.0827],
        [-0.1605],
        [-0.1319],
        [ 0.6141],
        [-1.3707],
        [-1.5465],
        [-2.2483],
        [ 0.2491],
        [ 1.0481],
        [-0.5747],
        [ 0.8528],
        [ 1.7696],
        [-0.5454],
        [ 0.0500],
        [-0.6747],
        [-0.5886],
        [-1.0642],
        [ 0.2386],
        [-0.8379],
        [-1.1011],
        [ 0.6762],
        [ 1.0132],
        [ 0.7451],
        [ 0.0965],
        [-0.0241],
        [ 0.0297],
        [-0.1095],
        [-0.5911],
        [-0.7688],
        [ 1.7096],
        [-0.4047],
        [-1.0249],
        [ 0.3773],
        [-0.9600],
        [ 1.4861],
        [-1.8635],
        [ 1.1082],
        [ 0.6791],
        [-0.6270],
        [-0.3563],
        [-0.5164],
        [-0.1545],
        [-0.2300],
        [-0.1974],
        [-0.6029],
        [-2.9157],
        [ 1.1194],
        [ 1.1679],
        [-1.6233],
        [ 1.3917],
        [ 0.4365],
        [ 0.8813],
        [-1.2441],
        [-2.4191],
        [-0.7130],
        [-0.0438],
        [-0.2678],
        [-0.2056],
        [ 1.9390],
        [-0.8739],
        [ 0.4379],
        [-0.6264],
        [ 1.1240],
        [ 1.3337],
        [-0.8554],
        [-0.4772],
        [-1.9145],
        [-0.3548],
        [-1.3139],
        [-1.1183],
        [-1.1850],
        [ 2.1581],
        [ 0.8458],
        [-0.2774],
        [ 0.6252],
        [-1.0238],
        [ 0.8846],
        [ 0.6432],
        [ 1.9761],
        [-0.5966],
        [ 0.4838],
        [ 0.9824],
        [ 0.1451],
        [ 0.2367],
        [-0.9718],
        [-0.3002],
        [-1.0239],
        [-1.3958],
        [ 1.4875],
        [-0.9238],
        [ 1.7886]]), 
 y: 
tensor([ 22.5139, -11.2928, -65.3266,  11.4912,  34.3622,  -4.7371,  55.7981,
         34.1948, -21.1198,   8.8681,   4.8401, -12.6738,  27.7491, -10.2920,
        -20.5800, -34.3397,  37.0163,  57.3231,   6.9397,  29.9672,  53.9756,
          4.4474,  20.7192,  -8.5406,   0.7447, -22.5050,   4.0683, -13.3933,
        -24.1197,  46.6569,  41.9460,  35.2172,   9.7509,  20.5186,  -3.9652,
          1.3670,   4.0815, -25.0052,  52.6946,  -5.1169, -14.0601,  26.0171,
        -16.5974,  65.3023, -37.8152,  37.5357,  31.6372,   0.7058,  -2.9643,
         17.8506,  15.1214,   6.6686,   4.1857,  16.1612, -72.6875,  44.3273,
         54.4379, -14.8631,  46.8485,  27.7344,  48.8398, -20.5679, -49.2582,
        -10.4936,  22.0268,   7.2506,   0.7285,  67.7584,  -7.8556,  26.0243,
         -3.9790,  58.8114,  36.1283, -12.2570,  -9.5121, -25.5052,  10.3903,
        -24.5829, -24.2417, -22.2563,  72.4724,  36.7423,   7.3779,  38.3146,
        -25.6796,  46.2081,  23.3987,  69.0189,  -0.8138,  31.3881,  54.9516,
         12.6113,  18.8799, -16.6771,  23.5101, -23.1808, -24.6395,  56.1088,
        -22.2519,  67.3660]), 
 coef: 
27.478050549563925
轮数: 1, 平均损失值: 1009.3691929408482
轮数: 2, 平均损失值: 922.2345842633929
轮数: 3, 平均损失值: 808.2444051106771
轮数: 4, 平均损失值: 718.8717286246164
轮数: 5, 平均损失值: 643.5392150878906
轮数: 6, 平均损失值: 579.3592580159506
轮数: 7, 平均损失值: 527.1173407106984
轮数: 8, 平均损失值: 483.0425162996565
轮数: 9, 平均损失值: 447.5422193739149
轮数: 10, 平均损失值: 416.84386073521205
轮数: 11, 平均损失值: 390.22895377022877
轮数: 12, 平均损失值: 366.51838992890856
轮数: 13, 平均损失值: 346.1531023297991
轮数: 14, 平均损失值: 328.2744347708566
轮数: 15, 平均损失值: 314.65721203031995
轮数: 16, 平均损失值: 300.4427876813071
轮数: 17, 平均损失值: 289.32418499473766
轮数: 18, 平均损失值: 277.8224137321351
轮数: 19, 平均损失值: 267.5367243773955
轮数: 20, 平均损失值: 258.28885931287493
轮数: 21, 平均损失值: 250.0061663932541
轮数: 22, 平均损失值: 242.12868918381727
轮数: 23, 平均损失值: 235.6611079814271
轮数: 24, 平均损失值: 229.33430033638365
轮数: 25, 平均损失值: 223.1730099596296
轮数: 26, 平均损失值: 217.5849765945267
轮数: 27, 平均损失值: 212.3398045736646
轮数: 28, 平均损失值: 207.5702041898455
轮数: 29, 平均损失值: 203.43085269270273
轮数: 30, 平均损失值: 199.51152138482956
轮数: 31, 平均损失值: 195.47343254968317
轮数: 32, 平均损失值: 191.71197933810097
轮数: 33, 平均损失值: 188.37182196084555
轮数: 34, 平均损失值: 185.11743242600386
轮数: 35, 平均损失值: 182.0129955525301
轮数: 36, 平均损失值: 179.1958266969711
轮数: 37, 平均损失值: 176.69069805660763
轮数: 38, 平均损失值: 174.17424527505287
轮数: 39, 平均损失值: 171.61573238163203
轮数: 40, 平均损失值: 169.23772202900477
轮数: 41, 平均损失值: 167.23570453497592
轮数: 42, 平均损失值: 165.2245652854037
轮数: 43, 平均损失值: 163.15937265288395
轮数: 44, 平均损失值: 161.16839787247892
轮数: 45, 平均损失值: 159.31715041266548
轮数: 46, 平均损失值: 157.59417141150243
轮数: 47, 平均损失值: 155.7813076376915
轮数: 48, 平均损失值: 154.45246794092515
轮数: 49, 平均损失值: 152.9874643040468
轮数: 50, 平均损失值: 151.4761284635748
轮数: 51, 平均损失值: 149.9691235730294
轮数: 52, 平均损失值: 148.51725063726798
轮数: 53, 平均损失值: 147.1526403913922
轮数: 54, 平均损失值: 145.79941011847012
轮数: 55, 平均损失值: 144.59512062552687
轮数: 56, 平均损失值: 143.57154455948242
轮数: 57, 平均损失值: 142.51473862291277
轮数: 58, 平均损失值: 141.46226671514253
轮数: 59, 平均损失值: 140.45422938704203
轮数: 60, 平均损失值: 139.35298119031248
轮数: 61, 平均损失值: 138.56872464329075
轮数: 62, 平均损失值: 137.59372400454663
轮数: 63, 平均损失值: 136.7332024043109
轮数: 64, 平均损失值: 135.845217436419
轮数: 65, 平均损失值: 135.060999251853
轮数: 66, 平均损失值: 134.20094066045502
轮数: 67, 平均损失值: 133.44674398332262
轮数: 68, 平均损失值: 132.6468291922527
轮数: 69, 平均损失值: 131.92499147722685
轮数: 70, 平均损失值: 131.13112634529872
轮数: 71, 平均损失值: 130.5510299612339
轮数: 72, 平均损失值: 129.86194417199917
轮数: 73, 平均损失值: 129.3868335827223
轮数: 74, 平均损失值: 128.72647036905454
轮数: 75, 平均损失值: 128.06132447367622
轮数: 76, 平均损失值: 127.34128719870758
轮数: 77, 平均损失值: 126.73475845304624
轮数: 78, 平均损失值: 126.18749061860008
轮数: 79, 平均损失值: 125.62511158668542
轮数: 80, 平均损失值: 125.00944049177426
轮数: 81, 平均损失值: 124.42087965488854
轮数: 82, 平均损失值: 124.00697353399174
轮数: 83, 平均损失值: 123.5078779685723
轮数: 84, 平均损失值: 122.90310735838348
轮数: 85, 平均损失值: 122.49766638689682
轮数: 86, 平均损失值: 121.9378119028882
轮数: 87, 平均损失值: 121.4568032927701
轮数: 88, 平均损失值: 120.94073245190567
轮数: 89, 平均损失值: 120.47416436337353
轮数: 90, 平均损失值: 120.00570991521789
轮数: 91, 平均损失值: 119.60176794036778
轮数: 92, 平均损失值: 119.16353989600765
轮数: 93, 平均损失值: 118.8740628713287
轮数: 94, 平均损失值: 118.39585426793997
轮数: 95, 平均损失值: 117.9782213102606
轮数: 96, 平均损失值: 117.54533132688985
轮数: 97, 平均损失值: 117.14753340753083
轮数: 98, 平均损失值: 116.73364404260938
轮数: 99, 平均损失值: 116.29547865075982
轮数: 100, 平均损失值: 115.96961811125279
100 轮的平均损失分别为:[1009.3691929408482, 922.2345842633929, 808.2444051106771, 718.8717286246164, 643.5392150878906, 579.3592580159506, 527.1173407106984, 483.0425162996565, 447.5422193739149, 416.84386073521205, 390.22895377022877, 366.51838992890856, 346.1531023297991, 328.2744347708566, 314.65721203031995, 300.4427876813071, 289.32418499473766, 277.8224137321351, 267.5367243773955, 258.28885931287493, 250.0061663932541, 242.12868918381727, 235.6611079814271, 229.33430033638365, 223.1730099596296, 217.5849765945267, 212.3398045736646, 207.5702041898455, 203.43085269270273, 199.51152138482956, 195.47343254968317, 191.71197933810097, 188.37182196084555, 185.11743242600386, 182.0129955525301, 179.1958266969711, 176.69069805660763, 174.17424527505287, 171.61573238163203, 169.23772202900477, 167.23570453497592, 165.2245652854037, 163.15937265288395, 161.16839787247892, 159.31715041266548, 157.59417141150243, 155.7813076376915, 154.45246794092515, 152.9874643040468, 151.4761284635748, 149.9691235730294, 148.51725063726798, 147.1526403913922, 145.79941011847012, 144.59512062552687, 143.57154455948242, 142.51473862291277, 141.46226671514253, 140.45422938704203, 139.35298119031248, 138.56872464329075, 137.59372400454663, 136.7332024043109, 135.845217436419, 135.060999251853, 134.20094066045502, 133.44674398332262, 132.6468291922527, 131.92499147722685, 131.13112634529872, 130.5510299612339, 129.86194417199917, 129.3868335827223, 128.72647036905454, 128.06132447367622, 127.34128719870758, 126.73475845304624, 126.18749061860008, 125.62511158668542, 125.00944049177426, 124.42087965488854, 124.00697353399174, 123.5078779685723, 122.90310735838348, 122.49766638689682, 121.9378119028882, 121.4568032927701, 120.94073245190567, 120.47416436337353, 120.00570991521789, 119.60176794036778, 119.16353989600765, 118.8740628713287, 118.39585426793997, 117.9782213102606, 117.54533132688985, 117.14753340753083, 116.73364404260938, 116.29547865075982, 115.96961811125279]
模型的权重：Parameter containing:
tensor([[27.6330]], requires_grad=True), 
模型的偏置：Parameter containing:
tensor([13.8751], requires_grad=True)

Process finished with exit code 0