数据结构与算法 B树

B树

特点

B树（B-tree、B-树）

• B树是一种平衡的多路搜索树，多用于文件系统、数据库的实现
• 1个节点可以存储超过2个元素、可以拥有超过2个节子节点
• 拥有二叉搜索树的一些性质（左子树都比根节点小 右子树都比根节点大）
• 平衡，每个节点的所有子树高度一致
• 比较矮

 

   

 

M阶B树的性质（M>=2）

• 假设一个节点存储的元素个数为x，根节点：1<= x <=m-1 ，非根节点： 「m/2」 - 1 <= x <=m-1
• 如果有子节点，因为节点有两个元素的话，那么它的字节点可以最多分出2+1个字节点， 因此 字节点个数 y = x +1 ,根节点的字节点个数 ： 2<=y<=m ，非根节点的子节点个数：「m.2」<=y<=m

          比如m = 3 ， 2<=y<=3 ，因此可以称为（2，3）树、2-3树

          比如m=4，2<=y<=4，因此可以称为（2，4）树、2-3-4树

 

 B树 vs 二叉搜索树

• B树和二叉搜索树，在逻辑上是等价的
• 多代节点合并，可以获得一个超级节点 。

        2代合并的超级节点，最多拥有4个子节点

        3代合并的超级节点，最多拥有8个子节点 

        n代合并的超级节点，最多拥有2^n个子节点，M阶B树，最多需要log2^m代合并    

             

      

为什么我们要引入B树呢？ 

B树的时间复杂度与二叉树一样，均为O(logN)。然而Ｂ树出现是因为磁盘ＩＯ。ＩＯ操作的效率很低，那么，当在大量数据存储中，查询时我们不能一下子将所有数据加载到内存中，只能逐一加载磁盘页，每个磁盘页对应树的节点。造成大量磁盘ＩＯ操作（最坏情况下为树的高度）。平衡二叉树由于树深度过大而造成磁盘IO读写过于频繁，进而导致效率低下。所以，我们为了减少磁盘ＩＯ的次数，就你必须降低树的深度，将“瘦高”的树变得“矮胖”。

 

B树搜索

跟二叉搜索树的搜索类似

• 先在节点内部从小到大开始搜索元素
• 如果命中，搜索结束
• 如果未命中，再去对应的子节点中搜索元素，重复步骤1

 

B树添加

• 新添加的元素必定是添加到叶子节点

                                                 

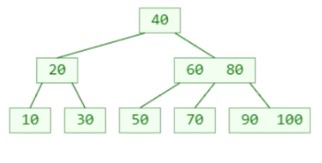
• 插入55 

                      

•  插入95

                                          

• 再插入98呢？假设这是一个4阶B树，那么节点最多能存储3个元素，那么此时最右下角的叶子节点元素个数将超过限制，这种现象可以称之为：上溢（overflow） 

上溢问题解决

• 上溢节点的元素个数必然等于m
• 假设上溢节点最中间元素的位置k ,将k位置的元素向上与父节点合并，将【0，k-1】和【k+1,m-1】位置的元素分裂成2个子节点，这2个子节点的元素个数，必然都不会低于最低限制（「m/2」-1）
• 一次分裂完毕后，有可能导致父节点上溢，依然按照上述方法解决，最极端的情况，有可能一直分裂到根节点

      

                                                               

B树删除

非叶子节点

•  先找到前驱节点或者后继节点，覆盖所需删除的元素的值

• 再把前驱或者后继元素删除

   删除60

   

• 非叶子节点的前驱 或后继元素，必定在叶子节点

       所以这里的删除前驱或者后继元素，就是最开始提到的情况：删除元素的叶子节点

       真正的删除元素都是发生在叶子节点

下溢 

• 下溢节点元素额数量必然等于「m/2」-2
• 如果下溢节点临近的兄弟节点，有至少「m/2」个元素，可以向其借一个元素 

          将父节点的元素b插入到下溢节点的0位置（最小位置）

          用兄弟节点的元素a（最大的元素）代替父节点的元素b

          这种操作其实就是旋转

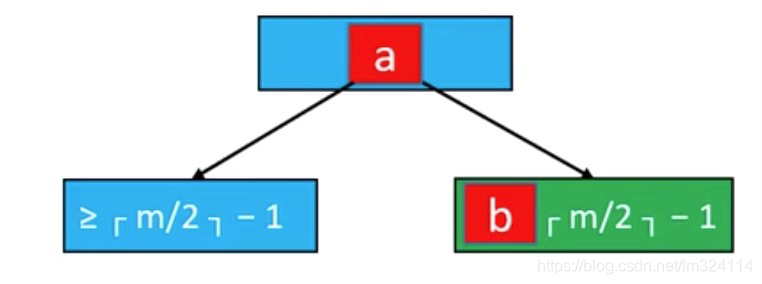
• 如果下溢节点临近的兄弟节点，只有「m/2」-1个元素 

      将父节点的元素b挪下来跟左右子节点进行合并 

      合并后的节点元素个数等于「m/2」+ 「m/2」-2 ,不超过m-1

  

• 这个操作可能导致父节点下溢，依然按照上述方法处理，下溢现象可能会一直往上传播