C++ | 动态规划（线性DP）DP入门学习

目录

理解记忆化

 什么时候用DP

---

理解记忆化

动态规划的底层逻辑思想是记忆化 ，就是说对于重复的过程不再进行重复计算，并且有时候仅通过贪心不能够实现结果最优，此时就需要用到动态规划来解决。

下面是记忆化的斐波那契数列的解法，如果单用递归可能50往后的数就难以快速得出结果了，但是记忆化5000也是可以快速得出结论的。

#include <bits/stdc++.h>
using namespace std;
using ll = long long;
const ll p = 1e9 + 7;
const int N = 1e5 + 3;
ll dp[N];

ll f(int n) 
{
	if (n <= 2) return 1;
	if (dp[n] != -1) return dp[n];

	return dp[n] = (f(n - 1) + f(n - 2)) % p;

}

int main() 
{
	memset(dp, -1, sizeof dp);
	int n;
	cin >> n;
	cout << f(n) << '\n';
	return 0;
}

 什么时候用DP

当一般题中出现有方案数/最小代价/最大价值，可以考虑使用。

状态是dp[i][j] 的取值，状态转移是状态与状态之间的转移关系，转移方向表示了迭代或递归方向。

题解：设状态dp[ i ][ j ] 表示从第i行第j列的元素往下走的所有路径当中最大的和，这代码当中 dp[ i ][ j ] 就是在维护最大的和 ，最后输出dp[1][1]。

我最初没想明白为什么是dp[1][1]，因为从下往上遍历，且每次取的都是最大值，到最上边就剩下一个dp[1][1]，所以就是最大值了。

#include<bits/stdc++.h>
using namespace std;
using ll = long long;
const int N = 150;
ll a[N][N], dp[N][N];

int main()
{
  int n;cin >> n;
  for (int i = 1; i <= n ; i++)
    for (int j = 1; j <= i; j ++) cin >> a[i][j];

  for (int i = n ; i >= 1; i --)
    for (int j = 1; j <= i; j ++)
      //状态转移方程
      dp[i][j] = a[i][j] + max(dp[i + 1][j], dp[i + 1][j + 1]);
  cout << dp[1][1];

  return 0;

}

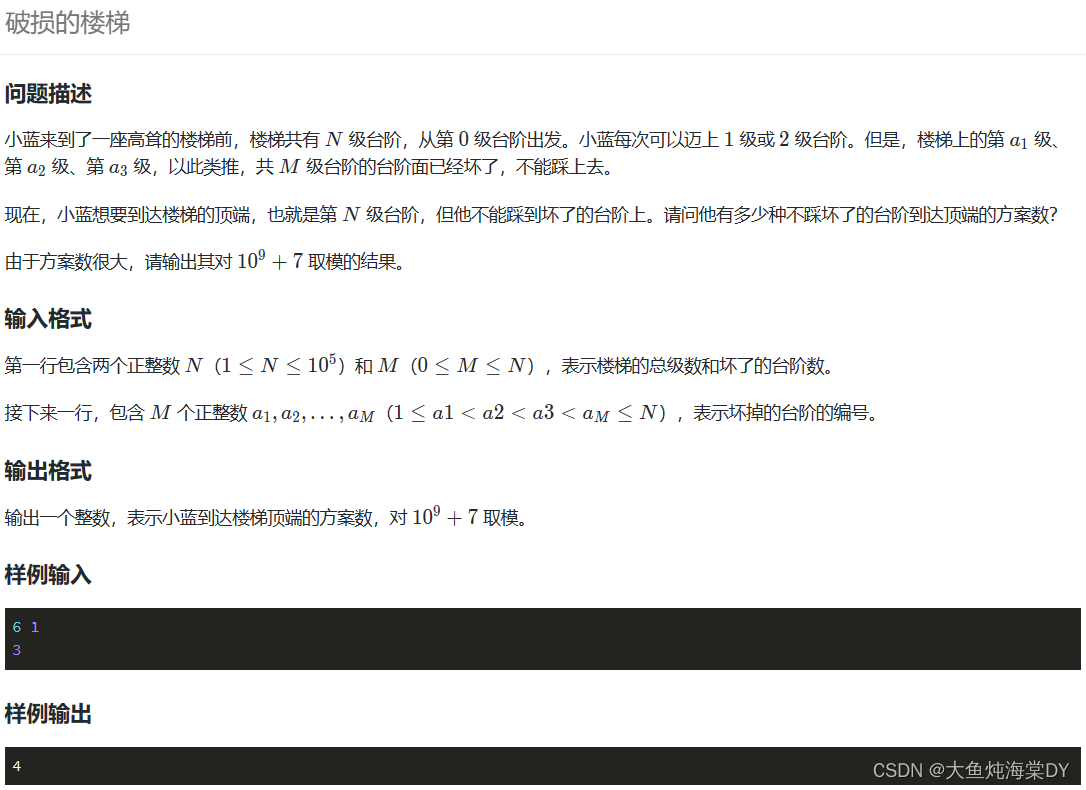
设状态dp[ i ] 表示走到底i级台阶，注意有一个0级台阶

状态转移方程为dp[ i ] = dp[ i - 1 ] + dp[ i - 2 ] ,若果i为破损的，则dp[ i ] = 0

用一个桶来记录那些位置是破损的

从前往后更新，最后输出dp[ n ]

注意零级台阶的初始值是1

#include <bits/stdc++.h>
using namespace std;
using ll = long long;
const int N = 1e5 + 9;
const ll p = 1e9 + 7;
ll dp[N];
bool broken[N];

int main()
{
  int n, m;cin >> n >> m;
  for (int i = 1; i <= m; i ++) 
  {
    int x;cin >> x;
    broken[x] = true;
  }

  dp[0] = 1;
  if (!broken[1]) dp[1] = 1;
  for (int i = 2; i <= n; i ++)
  {
    if (broken[i]) continue;
    dp[i] = (dp[i - 1] + dp[i - 2]) % p;
  }
  cout << dp[n];

  return 0;
}

 

 i - k - 1的意思是说这个数距上一个数的距离大于1的话，就说明还存在这样一个数可行就能继续往下走，否则结束。

#include<bits/stdc++.h>
using namespace std;
const int N = 1e6 + 9;
const int p = 1e9 + 7;
int prefix[N], dp[N];

int main()
{
  int n,k;cin >> n >> k;
  dp[0] = prefix[0] = 1;
  for (int i = 1; i <= n; i ++)
  {
    if (i - k - 1 < 1) dp[i] = 1;
    else dp[i] = prefix[i - k - 1];
    prefix[i] = (prefix[i - 1] + dp[i]) % p;
  }
  cout << prefix[n] << '\n';
  return 0;

}