集成学习——AdaBoost算法的理论与sklearn代码实现

1.集成学习

1.1 概念

  首先介绍一下什么是集成学习(Ensemble Learning)，通俗的讲，其思想就是"三个臭皮匠顶个诸葛亮"。在有监督的机器学习任务中，我们往往不容易得到一个完美的模型，这时就可以将几个不那么完美的模型结合起来来完成任务，这也是近年来各种竞赛(如kaggle、天池等)的优秀解决方案所采用的方法。这里的不那么完美的模型我们称为弱模型，多个弱模型结合起来得到的便是强模型。示意图如下：

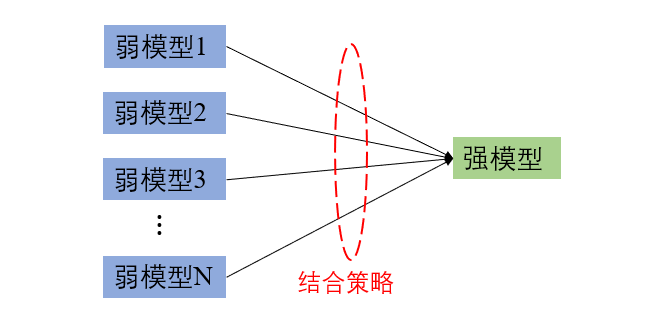
  集成学习潜在的思想是即便某一个弱模型得到了错误的预测，其他的弱模型也可以将错误纠正回来。

1.2 学习路线

  集成学习方法大致可以分为两大类，分别为Boosting和Bagging。

  Boosting是将弱模型提升为强模型的算法，其工作机制为：先从初始训练集训练出一个弱模型，再根据此弱模型的表现对训练样本的分布进行调整，使得被此弱模型预测错了的样本得到更多的关注，然后利用调整过的样本来训练下一个弱模型，如此重复进行，直到弱模型的数目达到了事先指定的值或者指标达到预期，最后将这些弱模型进行加权求和便得到了强模型。

  Bagging算法的工作机制为：通过自主采样法(bootstrap sampling)，即有放回的采样，对初始训练数据集进行采样，得到若干个样本子集，然后每个子集用来训练一个弱模型，最后再将这些弱模型结合为强模型。在分类任务中，Bagging算法通过简单投票法来输出样本的类别，即少数服从多数的原则；在回归任务中，则是通过对每个弱模型的输出进行平均来作为强模型的输出。

  通过对比Boosting算法与Bagging算法的工作机制可以发现：Boosting算法生成的弱模型有很强的依赖关系，且弱模型是串行生成的；而Bagging算法生成的弱模型不存在强依赖关系且可以并行生成。常见的Boosting算法有AdaBoost、GBDT、XGBoost和LightGBM等，最有代表性的Bagging算法为随机森林，如下图所示：

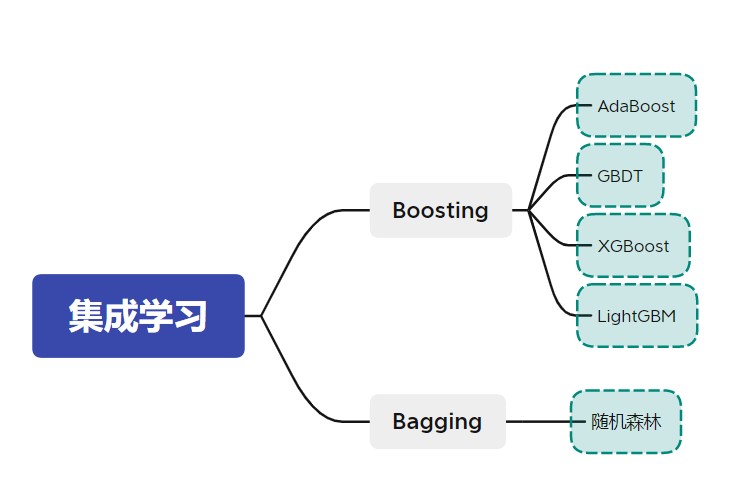
后面文章的内容将按上图由上至下的顺序展开。接下来我们就先介绍著名的AdaBoost算法。

2.AdaBoost算法

  AdaBoost是”Adaptive Boosting“（自适应增强）的缩写，由Yoav Freund和Robert Schapire在1995年提出。这里的自适应指的就是：前一个弱模型预测错误的样本的权值会增大，预测正确了的样本的权重会减小，即样本的权重可以自适应地更新，权值更新后的样本再次被用来训练下一个新的弱分类器。其实AdaBoost的思想在现实生活中也有体现，比如高考之前的刷题过程，拿到一套试卷，第一遍做的时候对每个题的关注程度都是相同的，后来再做第二遍第三遍的时候，往往都是着重关注第一次做错的题，而第一遍做对了的题看一遍就跳过了。

  下面以二类分类任务为例来讲解AdaBoost的原理。先给出AdaBoost的算法流程：

• 输入：训练数据集 T = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . , ( x N , y N ) } T=\{(\boldsymbol{x}_1,y_1),(\boldsymbol{x}_2,y_2),...,(\boldsymbol{x}_N,y_N)\} T={(x1​,y1​),(x2​,y2​),...,(xN​,yN​)}，其中${\mathbf{x}}_i\in R^n$， y i ∈ { − 1 , + 1 } y_i \in \{-1,+1\} yi​∈{−1,+1};弱学习算法。
• 输出：强分类器$G(x)$

(1) 初始化训练数据的权值分布：
$$D_1=(w_{11},w_{12},...,w_{1N})=(\frac{1}{N},\frac{1}{N},...,\frac{1}{N})$$
(2) 对$m=1,2,...,M$：

  (a)使用具有权值分布$D_m$的训练数据集学习，得到基本分类器$G_m(\mathbf{x})$。

  (b)计算$G_m(\mathbf{x})$在训练数据集上的分类误差率：
$$e_m=\sum _{i=1}^{N}P(G_m({\mathbf{x}}_i)\ne y_i)=\sum _{i=1}^N{w}_{mi}I(G_m({\mathbf{x}}_i)\ne y_i)$$
  ©计算$G_m(\mathbf{x})$在最终的强分类器$G(\mathbf{x})$中的重要程度，即$G_m(\mathbf{x})$的权重系数：
$${\alpha }_m=\frac{1}{2}\text{ln}\frac{1-e_m}{e_m}$$
  (d)更新训练数据集的权值分布：
$$D_{m+1}=(w_{m+1,1},w_{m+1,2},...,w_{m+1,N})$$
$$w_{m+1,i}=\frac{w_{mi}}{Z_m}\text{exp}(-{\alpha }_m{y}_i{G}_m({\mathbf{x}}_i))$$
其中$Z_m$是规范化因子，它使$D_{m+1}$成为一个概率分布：
$$Z_m=\sum _{i=1}^N{w}_{mi}\text{exp}(-{\alpha }_m{y}_i{G}_m({\mathbf{x}}_i))$$
(3) 构建基本分类器的线性组合：
$$f(\mathbf{x})=\sum _{i=1}^M{\alpha }_m{G}_m(\mathbf{x})$$
得到最终的强分类器：
$$G(\mathbf{x})=\text{sign}(f(x))=\text{sign}(\sum _{i=1}^M{\alpha }_m{G}_m(\mathbf{x}))$$
还是以一个例子来熟悉此算法过程，例子来源于李航《统计学习方法》。

对于上述的算法过程，我们需要搞清楚3个问题：

(1)为什么弱分类器$G_m(\mathbf{x})$的权重系数公式为${\alpha }_m=\frac{1}{2}\text{ln}\frac{1-e_m}{e_m}$?，这个式子是怎么得到的？

(2)为什么训练数据集的权值更新公式为$w_{m+1,i}=\frac{w_{mi}}{Z_m}\text{exp}(-{\alpha }_m{y}_i{G}_m({\mathbf{x}}_i))$?

(3)这样设置弱分类器的权重系数和权值更新公式真的能使模型的训练误差越来越小吗？

接下来我们将给出这3个问题的证明。

3.AdaBoost算法的损失函数优化

  首先给出损失函数的推导过程，我们知道初始训练数据集中第$i$个样本的权值$w_{1i}=\frac{1}{N}$,根据权值更新公式，则经过第一个弱分类器$G_1(\mathbf{x})$后，权值更新为$w_{2i}=\frac{1}{N}\cdot \frac{\text{exp}(-{\alpha }_1{y}_i{G}_1({\mathbf{x}}_i))}{Z_1}$；经过第$M$个弱分类器$G_M(\mathbf{x})$h后，权值更新为：
$$w_{M+1,i}=\frac{1}{N}\cdot \frac{\text{exp}(-{\alpha }_1{y}_i{G}_1({\mathbf{x}}_i))}{Z_1}\cdot ...\cdot \frac{\text{exp}(-{\alpha }_M{y}_i{G}_M({\mathbf{x}}_i))}{Z_M}$$
$$=\frac{\text{exp}(-({\alpha }_1{y}_i{G}_1({\mathbf{x}}_i)+...+{\alpha }_M{y}_i{G}_M({\mathbf{x}}_i)\left)\right)}{N{\prod }_{t=1}^M{Z}_m}$$
$$=\frac{\text{exp}(-y_i{\sum }_{m=1}^M{\alpha }_m{G}_m({\mathbf{x}}_i))}{N{\prod }_{m=1}^M{Z}_m}$$
$$=\frac{\text{exp}(-y_{i}f({\mathbf{x}}_i))}{N{\prod }_{m=1}^M{Z}_m}$$
通过上面的结果我们可以得到：
$$\frac{\text{exp}(-y_{i}f({\mathbf{x}}_i))}{N}=w_{M+1,i}\prod _{m=1}^M{Z}_m$$
这个式子后面马上就会用到。我们知道最终的强分类器的表达式为：$G(\mathbf{x})=\text{sign}(f(\mathbf{x}))$，如果第$i$个样本分类错误，即：$G({\mathbf{x}}_i)\ne y_i$，这等价于$y_{i}f({\mathbf{x}}_i)\le 0$，也就是说，当第$i$个样本被分类错误时，有：
$$\text{exp}(-y_{i}f({\mathbf{x}}_i))\ge 1\ge I(G({\mathbf{x}}_i)\ne y_i)$$
而强分类器的训练误差为：
$$\frac{1}{N}\sum _{i=1}^{N}I(G({\mathbf{x}}_i)\ne y_i)$$
于是我们可以得到：
$$\frac{1}{N}\sum _{i=1}^{N}I(G({\mathbf{x}}_i)\ne y_i)\le \sum _{i=1}^N\frac{\text{exp}(-y_{i}f({\mathbf{x}}_i))}{N}$$
$$=\sum _{i=1}^N{w}_{M+1,i}\prod _{m=1}^M{Z}_m=\prod _{m=1}^M{Z}_m$$
最后一个的等号成立是因为所有样本的权值相加为1。这就说明了分类器的训练误差上界为${\prod }_{m=1}^M{Z}_m$，我们只要保证误差上界在训练过程中一直减小也就保证了误差是一直减小的。正常来讲，我们应该选择${\prod }_{m=1}^M{Z}_m$来作为损失函数，但是由于每一个弱分类器都是串行生成的，所以我们没办法同时得到$M$个弱分类器，也就无法利用这个损失函数。AdaBoost是对此进行了近似，只要保证每一个分类器的$Z_m$最小，那么最终的${\prod }_{m=1}^M{Z}_m$也就达到了最小。也就是说，AdaBoost优化的损失函数即为：
$$Z_m=\sum _{i=1}^N{w}_{mi}\text{exp}(-{\alpha }_m{y}_i{G}_m({\mathbf{x}}_i))$$
  有了损失函数之后，我们就可以来解决上文所提到的三个问题了。

问题1：为什么弱分类器$G_m(\mathbf{x})$的权重系数公式为${\alpha }_m=\frac{1}{2}\text{ln}\frac{1-e_m}{e_m}$?，这个式子是怎么得到的？

在此问题中，首先需要明确我们的目标是最小化损失函数$Z_m$，即：
$${}_{{\alpha }_m,G_m(\mathbf{x})}^{\text{min}}\sum _{i=1}^N{w}_{mi}\text{exp}(-{\alpha }_m{y}_i{G}_m({\mathbf{x}}_i))$$
因为分类器的输出只有两种结果，要么分对，要么分错，即：
$$y_i{G}_m({\mathbf{x}}_i)=\{\begin{array}{ll}+1,& \text{if}{y}_i=G_m({\mathbf{x}}_i)\\ -1,& \text{if}{y}_i\ne G_m({\mathbf{x}}_i)\end{array}$$
所以可以将目标函数改写为：
$${}_{{\alpha }_m,G_m(\mathbf{x})}^{\text{min}}\sum _{y_i=G_m({\mathbf{x}}_i)}{w}_{mi}\text{exp}(-{\alpha }_m)+\sum _{y_i\ne G_m({\mathbf{x}}_i)}{w}_{mi}\text{exp}({\alpha }_m)$$
对${\alpha }_m$求导数，并令导数等于0：
$$-\text{exp}(-{\alpha }_m)\sum _{y_i=G_m({\mathbf{x}}_i)}{w}_{mi}+\text{exp}({\alpha }_m)\sum _{y_i\ne G_m({\mathbf{x}}_i)}{w}_{mi}=0$$
两边同乘$\text{exp}({\alpha }_m)$并移项：
$$\text{exp}(2{\alpha }_m)\sum _{y_i\ne G_m({\mathbf{x}}_i)}{w}_{mi}=\sum _{y_i=G_m({\mathbf{x}}_i)}{w}_{mi}$$
$$\text{exp}(2{\alpha }_m)=\frac{{\sum }_{y_i=G_m({\mathbf{x}}_i)}{w}_{mi}}{{\sum }_{y_i\ne G_m({\mathbf{x}}_i)}{w}_{mi}}$$
$$=\frac{1-{\sum }_{y_i\ne G_m({\mathbf{x}}_i)}{w}_{mi}}{{\sum }_{y_i\ne G_m({\mathbf{x}}_i)}{w}_{mi}}$$
$$=\frac{1-{\sum }_{i=1}^N{w}_{mi}I(G_m({\mathbf{x}}_i)\ne y_i)}{{\sum }_{i=1}^N{w}_{mi}I(G_m({\mathbf{x}}_i)\ne y_i)}$$
$$=\frac{1-e_m}{e_m}$$
所以使目标函数最小的${\alpha }_m$就是：
$${\alpha }_m^{\ast }=\frac{1}{2}\text{ln}\frac{1-e_m}{e_m}$$
问题2：为什么训练数据集的权值更新公式为$w_{m+1,i}=\frac{w_{mi}}{Z_m}\text{exp}(-{\alpha }_m{y}_i{G}_m({\mathbf{x}}_i))$?

这个问题的证明是从前向分步算法的角度来证明的，AdaBoost算法是前向分步算法的一个特例。证明过程参考李航《统计学习方法》P164。

问题3：这样设置弱分类器的权重系数和权值更新公式真的能使模型的训练误差越来越小吗？

为了证明方便，我们新定义一个变量$r$,其与分类误差率的关系为：
$$r=\frac{1}{2}-e_m$$
我们前面已经给出了每一个弱分类器的损失函数$Z_m$,即：
$$Z_m=\sum _{i=1}^N{w}_{mi}\text{exp}(-{\alpha }_m{y}_i{G}_m({\mathbf{x}}_i))$$
$$=\sum _{y_i=G_m({\mathbf{x}}_i)}{w}_{mi}\text{exp}(-{\alpha }_m)+\sum _{y_i\ne G_m({\mathbf{x}}_i)}{w}_{mi}\text{exp}({\alpha }_m)$$
$$=(1-e_m)\text{exp}(-{\alpha }_m)+e_m\text{exp}({\alpha }_m)$$
将${\alpha }_m^{\ast }=\frac{1}{2}\text{ln}\frac{1-e_m}{e_m}$和$r=\frac{1}{2}-e_m$代入上式可得：
$$Z_m=(1-e_m)\sqrt{\frac{e_m}{1-e_m}}+e_m\sqrt{\frac{1-e_m}{e_m}}$$
$$=2\sqrt{e_m(1-e_m)}$$
$$=\sqrt{1-4r^2}$$
由于$r=\frac{1}{2}-e_m$，所以有$-\frac{1}{2}\le r\le \frac{1}{2}$，所以$\sqrt{1-4r^2}\le 1$，即$Z_m\le 1$。我们在前面已经推导了最后强分类器的训练误差上界其实为${\prod }_{m=1}^M{Z}_m$，此处我们又证明了每一个$Z_m$都是小于等于1的，所以，这样设置弱分类器的权重系数，随着弱分类器的增多，训练误差上界确实是越来越小的。

4. AdaBoost的sklearn实现

首先导入要用的包：

import numpy as np
import pandas as pd
import seaborn as sns
from sklearn.preprocessing import LabelEncoder
from sklearn.ensemble import AdaBoostClassifier
from sklearn.tree import DecisionTreeClassifier
import matplotlib.pyplot as plt
%matplotlib inline

然后加载数据集，使用的还是iris数据集：

iris = sns.load_dataset("iris")
iris

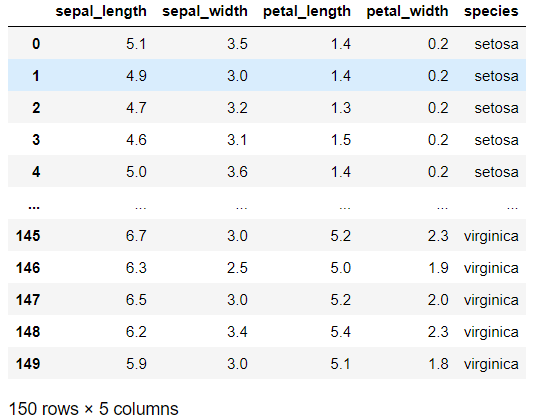
iris数据共3个类别，每个类别有50个样本，且有4个特征。为了做二分类并便于可视化，这里只使用了前100个样本和前两个特征。

获得所需数据并标签进行编码：

X = iris.iloc[:100].iloc[:,[0,1]]
y = iris.iloc[:100].iloc[:,-1]
encoder = LabelEncoder()
y = encoder.fit_transform(y) #将标签设置为0，1, 2样式

画出散点图：

X = np.array(X)
y = np.array(y)
plt.scatter(X[:,0],X[:,1],c=y)
plt.show()

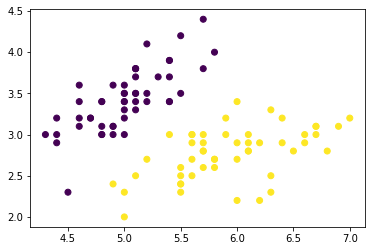
定义弱分类器:

#设定弱分类器CART，每个树的最大深度设置为2
weakClassifier=DecisionTreeClassifier(max_depth=2)

构建AdaBoost分类模型并进行训练

clf=AdaBoostClassifier(base_estimator=weakClassifier,algorithm='SAMME',n_estimators=300,learning_rate=0.8)
clf.fit(X, y)

生成测试数据：

x1_min=X[:,0].min()-1
x1_max=X[:,0].max()+1
x2_min=X[:,1].min()-1
x2_max=X[:,1].max()+1
x1_,x2_=np.meshgrid(np.arange(x1_min,x1_max,0.02),np.arange(x2_min,x2_max,0.02))

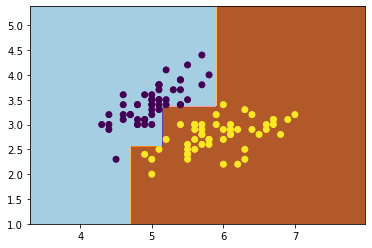
得出预测结果并可视化：

y_=clf.predict(np.c_[x1_.ravel(),x2_.ravel()]) # ravel函数将二维数组扁平化为一维
y_=y_.reshape(x1_.shape)
plt.contourf(x1_,x2_,y_,cmap=plt.cm.Paired)
plt.scatter(X[:,0],X[:,1],c=y)
plt.show()

5.补充

  本文只是针对分类任务来讲解AdaBoost，AdaBoost也是可以做回归的。前面还有一个问题没有提到，就是弱学习器的类型。理论上任何学习器都可以用于Adaboost.但一般来说，使用最广泛的Adaboost弱学习器是决策树和神经网络。对于决策树，Adaboost分类用了CART分类树，而Adaboost回归用了CART回归树。上面代码中使用的弱分类器就是CART分类决策树。

AdaBoost算法的优缺点：

优点：

• Adaboost作为分类器时，分类精度很高；

• 在Adaboost的框架下，可以使用各种回归分类模型来构建弱学习器，非常灵活；

• 作为简单的二元分类器时，构造简单，结果可理解；

• 不容易发生过拟合。

缺点：

• 对异常样本敏感，异常样本在迭代中可能会获得较高的权重，影响最终的强学习器的预测准确性。

6.参考资料

1.李航《统计学习方法》

2.周志华《机器学习》

3.https://www.cnblogs.com/pinard/p/6133937.html#!comments

4.https://www.bilibili.com/video/BV1mt411a7FT?p=4

5.https://www.bilibili.com/video/BV1Ca4y1t7DS?p=7

6.https://github.com/BackyardofAbela/EnsembleLearning

推荐阅读：
决策树(2)——CART算法
决策树(1)——ID3算法与C4.5算法的理论基础与python实现

公众号：MyLearningNote