1.前言
感知机在1957年由Rosenblatt提出,是支持向量机和神经网络的基础。感知机是一种二类分类的线性分类模型,输入为实例的特征向量,输出为实例的类别,正类取1,负类取-1。感知机是一种判别模型,其目标是求得一个能够将数据集中的正实例点和负实例点完全分开的分离超平面。如果数据不是线性可分的,则最后无法获得分离超平面。
2.模型
假设模型的输入为$ \boldsymbol{x}\in R^n$,输出为{+1,-1},则模型可以表示为:
f
(
x
)
=
sign
(
w
⋅
x
+
b
)
f(\boldsymbol{x})=\text{sign}(\boldsymbol{w} \cdot \boldsymbol{x}+b)
f(x)=sign(w⋅x+b)
sign ( z ) = { + 1 , if z ≥ 0 − 1 , if z < 0 \text{sign}(z) = \begin{cases} +1 ,&\text{if} \enspace z \ge 0 \\ -1 ,&\text{if} \enspace z<0 \end{cases} sign(z)={+1,−1,ifz≥0ifz<0
其中 w \boldsymbol{w} w和 b b b为感知机的模型参数, f ( x ) f(x) f(x)即为要求的分离超平面。图1为感知机模型的示意图, w ⋅ x + b = 0 \boldsymbol{w} \cdot \boldsymbol{x}+b=0 w⋅x+b=0即为一个超平面。
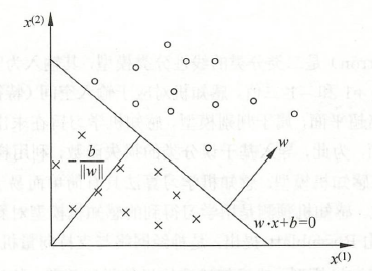
感知机学习时,由训练数据集 T = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . , ( x N , y N ) } T=\{(\boldsymbol{x_1},y_1),(\boldsymbol{x_2},y_2),...,(\boldsymbol{x_N},y_N)\} T={(x1,y1),(x2,y2),...,(xN,yN)},其中 x 1 ∈ R n \boldsymbol{x_1}\in R^n x1∈Rn, y i ∈ { + 1 , − 1 } y_i \in \{+1,-1\} yi∈{+1,−1}, i = 1 , 2 , 3 , . . . . , N i=1,2,3,....,N i=1,2,3,....,N,求得感知机模型 f ( x ) f(\boldsymbol{x}) f(x)。感知机预测时,通过训练好的 f ( x ) f(\boldsymbol{x}) f(x)判别新的输入实例的类别。
3.损失函数
为了求得分离超平面,需要构建一个损失函数,并通过极小化此损失函数来求得模型参数 w \boldsymbol{w} w和 b b b。感知机的损失函数为所有误分类点到超平面的距离之和。首先写出输入空间 R n R^n Rn任一实例点到 x 0 \boldsymbol{x_0} x0分离超平面的距离 d d d,即图2中的红线长度:
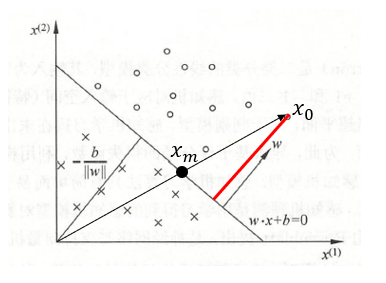
d
d
d即为向量
∣
x
0
−
x
m
∣
|\boldsymbol{x_0}-\boldsymbol{x_m}|
∣x0−xm∣在超平面的单位法向量
w
∣
∣
w
∣
∣
\frac{\boldsymbol{w}}{||\boldsymbol{w}||}
∣∣w∣∣w上的投影长度,则距离的表达式可以写为:
d
=
w
∣
∣
w
∣
∣
⋅
∣
x
0
−
x
m
∣
=
∣
w
⋅
x
0
−
w
⋅
x
m
∣
∣
∣
w
∣
∣
=
∣
w
⋅
x
0
−
w
⋅
x
m
−
b
+
b
∣
∣
∣
w
∣
∣
=
∣
w
⋅
x
0
+
b
∣
∣
∣
w
∣
∣
d=\frac{\boldsymbol{w}}{||\boldsymbol{w}||} \cdot |\boldsymbol{x_0}-\boldsymbol{x_m}| =\frac{|\boldsymbol{w \cdot x_0-w \cdot x_m}|}{||\boldsymbol{w}||} =\frac{|\boldsymbol{w \cdot x_0-w \cdot x_m}- b + b|}{||\boldsymbol{w}||} =\frac{|\boldsymbol{w \cdot x_0}+b|}{||\boldsymbol{w}||}
d=∣∣w∣∣w⋅∣x0−xm∣=∣∣w∣∣∣w⋅x0−w⋅xm∣=∣∣w∣∣∣w⋅x0−w⋅xm−b+b∣=∣∣w∣∣∣w⋅x0+b∣
当正类误分类为负类时,即当
y
i
=
1
y_i=1
yi=1,
f
(
x
i
)
<
0
f(\boldsymbol{x_i})<0
f(xi)<0时,有
−
y
i
(
w
⋅
x
i
+
b
)
>
0
-y_i(\boldsymbol{w} \cdot \boldsymbol{x_i}+b)>0
−yi(w⋅xi+b)>0,
当负类误分类为正类时,即当
y
i
=
−
1
y_i=-1
yi=−1,
f
(
x
i
)
>
0
f(\boldsymbol{x_i})> 0
f(xi)>0时,有
−
y
i
(
w
⋅
x
i
+
b
)
>
0
-y_i(\boldsymbol{w} \cdot \boldsymbol{x_i}+b) > 0
−yi(w⋅xi+b)>0。所以,误分类点到超平面的距离为:
d
=
−
y
i
(
w
⋅
x
i
+
b
)
∣
∣
w
∣
∣
d=-\frac{y_i(\boldsymbol{w} \cdot \boldsymbol{x_i}+b)}{||\boldsymbol{w}||}
d=−∣∣w∣∣yi(w⋅xi+b)
假设误分类点的集合为M,则所有误分类点到超平面的距离总和为:
−
∑
x
i
∈
M
y
i
(
w
⋅
x
i
+
b
)
∣
∣
w
∣
∣
-\frac{\displaystyle\sum_{\boldsymbol{x_i} \in M}y_i(\boldsymbol{w} \cdot \boldsymbol{x_i}+b)}{||\boldsymbol{w}||}
−∣∣w∣∣xi∈M∑yi(w⋅xi+b)
不考虑
1
∣
∣
w
∣
∣
\frac{1}{||\boldsymbol{w}||}
∣∣w∣∣1,就得到了感知机的损失函数:
L
(
w
,
b
)
=
−
∑
x
i
∈
M
y
i
(
w
⋅
x
i
+
b
)
L(\boldsymbol{w},b)=-\displaystyle\sum_{\boldsymbol{x_i} \in M}y_i(\boldsymbol{w} \cdot \boldsymbol{x_i}+b)
L(w,b)=−xi∈M∑yi(w⋅xi+b)
4.感知机的学习算法
要求得模型参数
w
\boldsymbol{w}
w和
b
b
b,需要极小化损失函数,即:
m
i
n
w
,
b
L
(
w
,
b
)
=
−
∑
x
i
∈
M
y
i
(
w
⋅
x
i
+
b
)
min_{\boldsymbol{w},b}L(\boldsymbol{w},b)=-\displaystyle\sum_{\boldsymbol{x_i} \in M}y_i(\boldsymbol{w} \cdot \boldsymbol{x_i}+b)
minw,bL(w,b)=−xi∈M∑yi(w⋅xi+b)
极小化的过程采用随机梯度下降算法(stochastic gradient descent, SGD)来实现,首先任意选取一个超平面
w
0
,
b
0
\boldsymbol{w_0},b_0
w0,b0,然后找出误分类点,每次随机选取一个误分类点来进行梯度下降,进而对
w
\boldsymbol{w}
w和
b
b
b进行更新,直到没有误分类点:
w
=
w
+
η
y
i
x
i
\boldsymbol{w}=\boldsymbol{w}+\eta y_i \boldsymbol{x_i}
w=w+ηyixi
b
=
b
+
η
y
i
b=b+\eta y_i
b=b+ηyi
其中,
η
(
0
<
η
≤
1
)
\eta(0<\eta \le 1)
η(0<η≤1)为学习率。
4.1 感知机学习算法的原始形式
-
输入:
训练数据集 T = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . , ( x N , y N ) } T=\{(\boldsymbol{x_1},y_1),(\boldsymbol{x_2},y_2),...,(\boldsymbol{x_N},y_N)\} T={(x1,y1),(x2,y2),...,(xN,yN)}, 其中 x 1 ∈ R n \boldsymbol{x_1}\in R^n x1∈Rn, y i ∈ { + 1 , − 1 } y_i \in \{+1,-1\} yi∈{+1,−1}, i = 1 , 2 , 3 , . . . . , N i=1,2,3,....,N i=1,2,3,....,N,学习率 η ( 0 < η ≤ 1 ) \eta(0<\eta \le 1) η(0<η≤1)。 -
输出:
w , b \boldsymbol{w},b w,b; 感知机模型 f ( x ) = sign ( w ⋅ x + b ) f(x)=\text{sign}(\boldsymbol{w \cdot x}+b) f(x)=sign(w⋅x+b) -
算法流程:
- 选取初值: w 0 , b 0 \boldsymbol{w_0},b_0 w0,b0;
- 在训练集中选取数据 ( x i , y i ) (x_i,y_i) (xi,yi);
- 如果
y
i
(
w
⋅
x
i
+
b
)
≤
0
y_i(\boldsymbol{w} \cdot \boldsymbol{x_i}+b) \le 0
yi(w⋅xi+b)≤0,
w = w + η y i x i \boldsymbol{w}=\boldsymbol{w}+\eta y_i \boldsymbol{x_i} w=w+ηyixi
b = b + η y i b=b+\eta y_i b=b+ηyi - 转至第2步,直至训练集中没有误分类点。
-
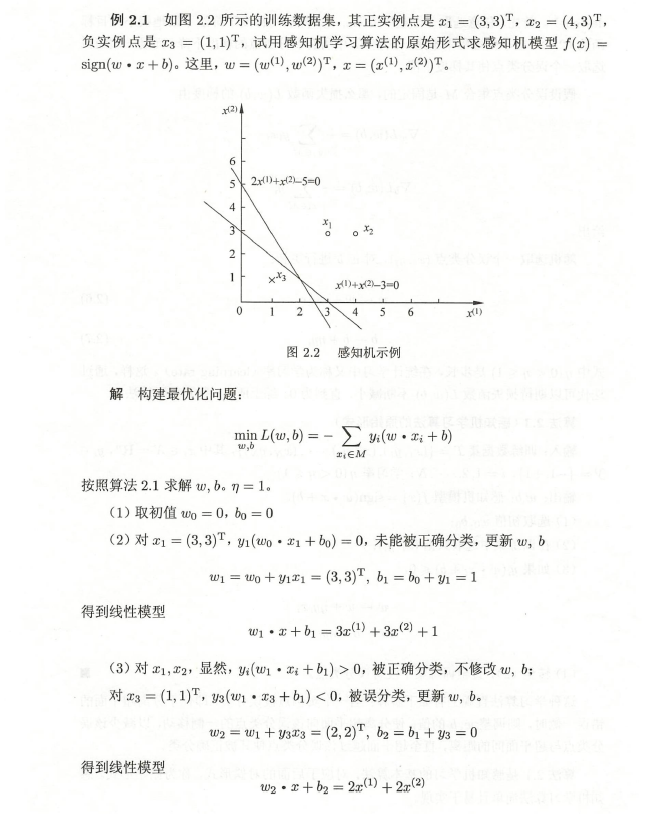
图3为李航《统计学习方法》中的例子。

4.2 感知机学习算法的对偶形式
对偶形式的基本想法是,将
w
\boldsymbol{w}
w和
b
b
b表示为实例
x
i
\boldsymbol{x_i}
xi和标记
y
i
y_i
yi的线性组合形式。设误分类点
(
x
i
,
y
i
)
(\boldsymbol{x_i},y_i)
(xi,yi)通过梯度下降算法对
w
\boldsymbol{w}
w和
b
b
b修改了
n
i
n_i
ni次,则
w
\boldsymbol{w}
w和
b
b
b关于
(
x
i
,
y
i
)
(\boldsymbol{x_i},y_i)
(xi,yi)的增量分别为
α
i
y
i
x
i
\alpha_iy_i\boldsymbol{x_i}
αiyixi和
α
i
y
i
\alpha_iy_i
αiyi,这里的
α
i
=
n
i
η
\alpha_i=n_i\eta
αi=niη。则最后学习到的
w
\boldsymbol{w}
w和
b
b
b可以分别表示为:
w
=
w
0
+
∑
i
=
1
N
α
i
y
i
x
i
\boldsymbol{w}=\boldsymbol{w_0}+\sum_{i=1}^{N}\alpha_iy_i\boldsymbol{x_i}
w=w0+i=1∑Nαiyixi
b
=
b
0
+
∑
i
=
1
N
α
i
y
i
b=b_0+\sum_{i=1}^{N}\alpha_iy_i
b=b0+i=1∑Nαiyi
- 输入:
训练数据集 T = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . , ( x N , y N ) } T=\{(\boldsymbol{x_1},y_1),(\boldsymbol{x_2},y_2),...,(\boldsymbol{x_N},y_N)\} T={(x1,y1),(x2,y2),...,(xN,yN)}, 其中 x 1 ∈ R n \boldsymbol{x_1}\in R^n x1∈Rn, y i ∈ { + 1 , − 1 } y_i \in \{+1,-1\} yi∈{+1,−1}, i = 1 , 2 , 3 , . . . . , N i=1,2,3,....,N i=1,2,3,....,N,学习率 η ( 0 < η ≤ 1 ) \eta(0<\eta \le 1) η(0<η≤1)。 - 输出:
α , b \boldsymbol{\alpha},b α,b;感知机模型 f ( x ) = sign ( w 0 + ∑ j = 1 N α j y j x j ⋅ x + b ) f(x)=\text{sign}(\boldsymbol{w_0}+\displaystyle\sum_{j=1}^{N}\alpha_jy_j\boldsymbol{x_j \cdot x}+b) f(x)=sign(w0+j=1∑Nαjyjxj⋅x+b),其中, α = ( α 1 , α 2 , . . . , α N ) T \boldsymbol{\alpha}=(\alpha_1,\alpha_2,...,\alpha_N)^T α=(α1,α2,...,αN)T,一般初值 w 0 \boldsymbol{w_0} w0取0。 - 算法流程:
- 选取初值: α = 0 , b = 0 \boldsymbol{\alpha}=0,b=0 α=0,b=0;
- 在训练集中选取数据 ( x i , y i ) (\boldsymbol{x_i},y_i) (xi,yi);
- 如果
y
i
(
∑
j
=
1
N
α
j
y
j
x
j
⋅
x
i
+
b
)
≤
0
y_i(\displaystyle\sum_{j=1}^{N}\alpha_jy_j\boldsymbol{x_j \cdot x_i}+b) \le 0
yi(j=1∑Nαjyjxj⋅xi+b)≤0,
α i = α i + η \alpha_i=\alpha_i+\eta\\ αi=αi+η
b = b + η y i b=b+\eta y_i b=b+ηyi - 转至第2步,直至没有误分类数据。
- 图4为李航《统计学习方法》中的例子。

5.代码实现
本文实现了感知机学习算法的原始形式,使用的数据集为iris数据集,数据集大小为150×5,前4列为特征,最后一列为标签,共有三种类别,每种类别有50行数据;由于感知机为二分类模型,所以这里只使用了前100行数据作为训练数据,并且选择sepal_length,sepal_width作为特征来进行训练,代码实现是在jupyter notebook中完成的,实现过程如下:
- 导入需要使用的包
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
- 加载并处理数据
加载数据:
iris = sns.load_dataset("iris")
iris.head() //打印数据前5行
| sepal_length | sepal_width | petal_length | petal_width | species | |
|---|---|---|---|---|---|
| 0 | 5.1 | 3.5 | 1.4 | 0.2 | setosa |
| 1 | 4.9 | 3.0 | 1.4 | 0.2 | setosa |
| 2 | 4.7 | 3.2 | 1.3 | 0.2 | setosa |
| 3 | 4.6 | 3.1 | 1.5 | 0.2 | setosa |
| 4 | 5.0 | 3.6 | 1.4 | 0.2 | setosa |
选择前100行数据:
df = iris.iloc[:100,[0, 1, -1]]
df
| sepal_length | sepal_width | species | |
|---|---|---|---|
| 0 | 5.1 | 3.5 | setosa |
| 1 | 4.9 | 3.0 | setosa |
| 2 | 4.7 | 3.2 | setosa |
| 3 | 4.6 | 3.1 | setosa |
| 4 | 5.0 | 3.6 | setosa |
| ... | ... | ... | ... |
| 95 | 5.7 | 3.0 | versicolor |
| 96 | 5.7 | 2.9 | versicolor |
| 97 | 6.2 | 2.9 | versicolor |
| 98 | 5.1 | 2.5 | versicolor |
| 99 | 5.7 | 2.8 | versicolor |
100 rows × 3 columns
标签编码:将标签变为0,1,2样式from sklearn.preprocessing import LabelEncoder
encoder = LabelEncoder()
df["species"] = encoder.fit_transform(df["species"])
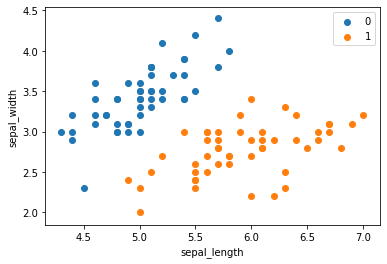
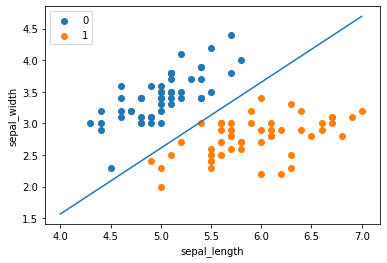
此时,可以画出将数据进行可视化,代码如下,可视化结果如图5所示:
plt.scatter(df[:50]['sepal_length'], df[:50]['sepal_width'], label='0')
plt.scatter(df[50:100]['sepal_length'], df[50:100]['sepal_width'], label='1')
plt.xlabel('sepal_length')
plt.ylabel('sepal_width')
plt.legend()
划分训练集与测试集:
from sklearn.model_selection import train_test_split
data = np.array(df)
X, y = data[:,:-1], data[:,-1]
y = np.array([1 if i == 1 else -1 for i in y])
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.1)
- 算法的实现
class Model:
def __init__(self):
#初始化w, b和学习率
self.w = np.ones(2, dtype=np.float32)
self.b = 0
self.l_rate = 0.01
def multiply(self, x, w, b):
y = np.dot(x, w) + b
return y
#模型训练,随机梯度下降
def model_fit(self, X_train, y_train):
print("start to fit")
flag = True
while flag:
wrong_count = 0
for i in range(len(X_train)):
X = X_train[i]
y = y_train[i]
if y * self.multiply(X, self.w, self.b) <= 0: #判别误分类点
self.w = self.w + self.l_rate * np.dot(y, X)
self.b = self.b + self.l_rate * y
wrong_count += 1
if wrong_count == 0:
flag = False
print("Model training completed!")
print("w = {}, b = {}".format(self.w, self.b)) #给出训练后的模型参数
#模型测试,给出正确率
def model_test(self, X_test, y_test):
print("start to test")
m = X_test.shape[0]
errorCnt = 0
for i in range(m):
X = X_test[i]
y = y_test[i]
if y * self.multiply(X, self.w, self.b) <= 0:
errorCnt += 1
accruRate = 1 - (errorCnt / m)
print("Model testing completed!")
print("Accuracy rate is {}".format(accruRate))
perceptron = Model()
perceptron.model_fit(X_train, y_train)
perceptron.model_test(X_test, y_test)
- 实验结果
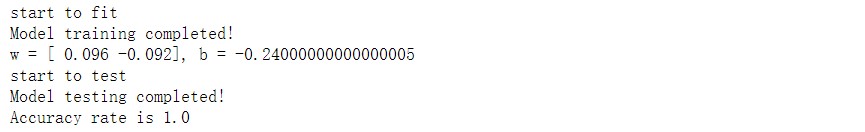





 本文详细介绍了感知机模型,包括其定义、损失函数、学习算法及其对偶形式,并提供了使用Python实现感知机的原始形式。通过 iris 数据集进行训练和测试,展示了感知机如何应用于实际问题。
本文详细介绍了感知机模型,包括其定义、损失函数、学习算法及其对偶形式,并提供了使用Python实现感知机的原始形式。通过 iris 数据集进行训练和测试,展示了感知机如何应用于实际问题。



















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










