对力扣：134.加油站中的贪心法的累加过程中出现负值需要将起点移动到当前下一个点尝试的原因进行反证法证明

题目链接

先上代码，这段代码是为了方便理解，所以写了两个循环，实际上可以把两个循环合并成一个循环，在一个循环里就可以完成这一件事，但是为了方便下文的讲解，所以有两个循环，后面优化成一个循环的代码见最后。

public int canCompleteCircuit(int[] gas, int[] cost) {
        int curSum=0;
        int total=0;

        for (int i = 0; i < gas.length; i++) {
            total+=gas[i]-cost[i];

        }
        if(total<0){    //总补充油量比总消耗量少，不可能可以跑完一圈
            return -1;
        }

        int start=0;    //记录起点
        int i=0;    //记录当前遍历下标
        while(i<gas.length){
            curSum+=gas[i]-cost[i];
            if(curSum<0){
                curSum=0;
                i++;
                start=i;
            }else {
                i++;
            }
        }
        return start;

    }

首先讲一下上述代码即这道题的贪心法的解题思路，题目的最终结果只有两种，一种是可以挑一个起点跑完一圈，另一种是哪个起点都不能跑完一圈，可以通过贪心法对加油站的补充油量和消耗油量进行贪心遍历累加得到最终结果，其中方法中定义了一个当前累加总和curSum变量，当前加油站的净累加油量（即补充油量减消耗油量的差值）如果为正值那么就一直累加，如果出现负值，那么我们就把curSum清零并选取当前遍历到的加油站的下一个站点作为起点再次尝试，下文中就通过反证法证明这样做的合理性，同时哪个起点都不能跑完一圈的判断在下文代码中有展示，本文对此不作过多说明。

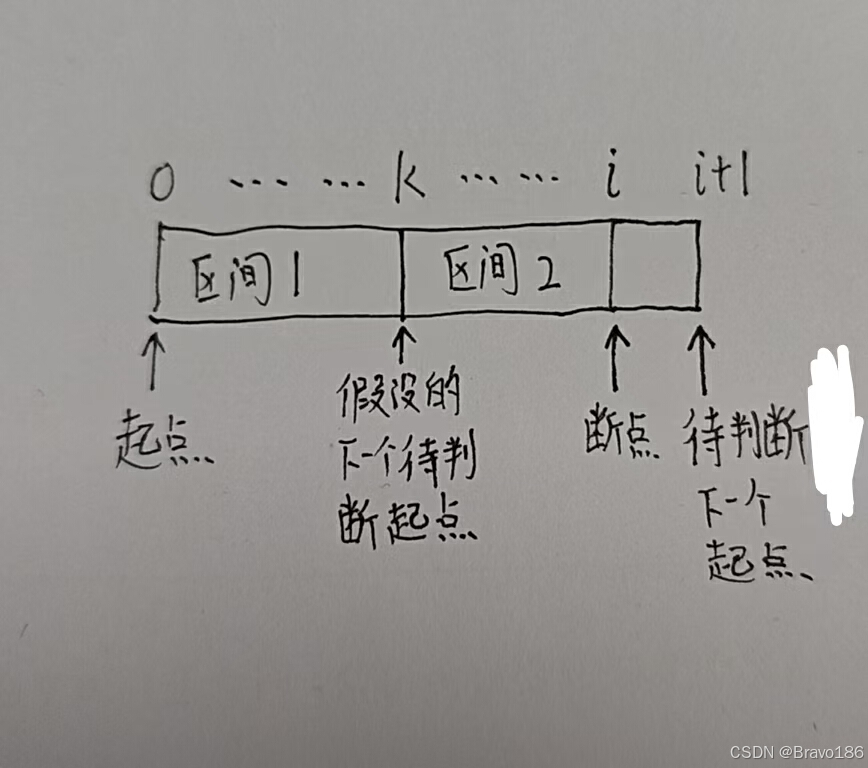
解法中可以看到，我们每次遍历到断点i的时候都是curSum已经<0，再把记录起点的start记为i+1，那为什么start就一定是i的下一个而不能是前面的点呢，万一选前面的点k也可以作为起点而中间的累加值不会出现<0的情况呢，下面开始进行反证。

假设我们不应该遇到curSum<0的时候就选择下一个点如i+1作为start，而是应该选择前面的某个点k作为start值，那么说明k点到i点的累加curSum值应该是>0的，而区间1和区间2的总和我们知道是<0的，所以区间1的总和一定是<0的，所以k点是刚遇到curSum<0的情况下的下一个点，而我们假设的是不应该遇到curSum<0的时候就选择下一个点作为start，但是k点又刚好是遇到curSum<0的时候的下一个点，这和我们的假设矛盾，所以推出结论：我们就是应该每遇到curSum<0的时候就选择下一个点作为start，证毕。

另外提供一下优化成一个循环的代码段

public int canCompleteCircuit(int[] gas, int[] cost) {
        int curSum=0;
        int total=0;
        int start=0;    //记录起点下标
        for (int i = 0; i < gas.length; i++) {
            curSum+=gas[i]-cost[i];
            total+=gas[i]-cost[i];
            if(curSum<0){
                curSum=0;
                //从下一个位置开始跑，可以通过反证法证明
                start=i+1;
            }
        }
        if(total<0){    //总补充油量比总消耗量少，不可能可以跑完一圈
            start=-1;
        }
        return start;
    }