HDU 4417 Super Mario (可持久化线段树)

 

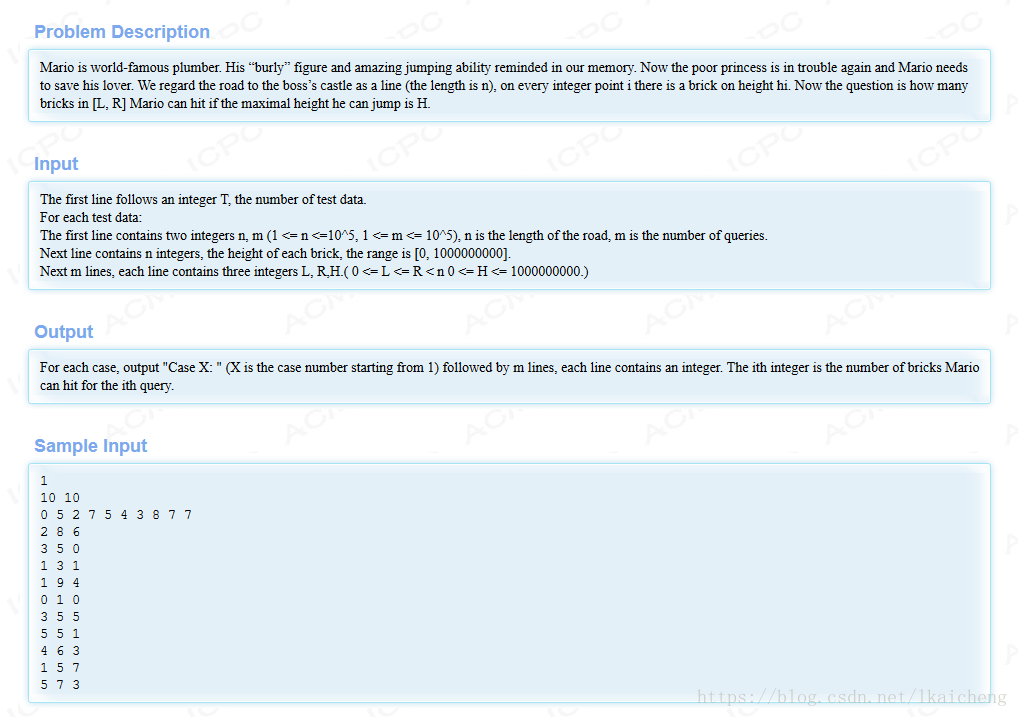
题意：马里奥顶砖块游戏   一条长为n的路 有n个砖块    给你n个砖块的高度   现有m个询问   每个询问为  l,r,h 表示在【l,r】这段路上  最高能跳h高 时能顶多少个砖块

思路：可持久化线段树 模板题    以每个高度建线段树 （要离散化） 以路上的位置为时间  将每个位置 单点更新  用size【i】记录这段上的点的个数  最后区间查询  1~h（此处h为 第一个小于等于h的数 离散后的值）的点的个数；

代码：

#include<cstdio>
#include<algorithm>
#include<iostream>
#include<cstring>
#include<cmath>
#include<map>
#include<set>
using namespace std;
typedef long long ll;
const int N=100005;
int tree[N],siz[N*25],lchild[N*25],rchild[N*25];
int tot;
map<int,int>mp,mp2;
set<int>se;
set<int>::iterator it;
void update(int cur,int last,int l,int r,int x)
{
    siz[cur]=siz[last];
    lchild[cur]=lchild[last];
    rchild[cur]=rchild[last];
    if(l==r)
    {
        siz[cur]++;
        return ;
    }
    int mid=(l+r)>>1;
    if(x<=mid)
    {
        update(lchild[cur]=++tot,lchild[last],l,mid,x);
    }
    else
    {
        update(rchild[cur]=++tot,rchild[last],mid+1,r,x);
    }
    siz[cur]=siz[lchild[cur]]+siz[rchild[cur]];
}
int query(int cur,int last,int l,int r,int nl,int nr)
{
    if(l==nl&&r==nr)
    {
        return siz[cur]-siz[last];
    }
    int mid=(l+r)>>1;
    if(mid<nl)
    {
        return query(rchild[cur],rchild[last],mid+1,r,nl,nr);
    }
    else if(mid>=nr)
    {
        return query(lchild[cur],lchild[last],l,mid,nl,nr);
    }
    else
    {
        return query(lchild[cur],lchild[last],l,mid,nl,mid)+query(rchild[cur],rchild[last],mid+1,r,mid+1,nr);
    }
}
int a[N],b[N];
int main()
{
    int t,n,m,cas;
    cas=0;
    scanf("%d",&t);
    while(t--)
    {
        cas++;
        mp.clear();
        se.clear();
        tot=0;
        scanf("%d%d",&n,&m);
        for(int i=0;i<n;i++)
        {
            scanf("%d",&a[i]);
            se.insert(a[i]);
        }
        int cnt=0;
        for(it=se.begin();it!=se.end();it++)
        {
            mp[*it]=++cnt;
        }
        for(int i=1;i<=n;i++)
        {
            tree[i]=++tot;
            update(tree[i],tree[i-1],1,n,mp[a[i-1]]);
        }
        printf("Case %d:\n",cas);
        for(int i=0;i<m;i++)
        {
            int l,r,h;
            scanf("%d%d%d",&l,&r,&h);
            l++;
            r++;
            it=se.upper_bound(h);
            if(it==se.end())  printf("%d\n",r-l+1);
            else
            {
                int zhi=*it;
                int wei=mp[zhi];
                if(wei==1) printf("0\n");
                else
                {
                    wei--;
                    printf("%d\n",query(tree[r],tree[l-1],1,n,1,wei));
                }
            }
        }
    }
    return 0;
}