并查集详解

并查集

一、什么是并查集

并查集是一种树型的数据结构，用于处理一些不相交集合的合并及查询问题。

并查集的思想是用一个数组表示了整片森林(parent)，树的根节点唯一标识了一个集合，我们只要找到了某个元素的的树根，就能确定它在哪个集合里。

1、并查集要一般处理的问题

(1)合并:将若干点合并到一个或多个集合(构成一棵树或多棵树)，将多个集合合并(多棵树合并为一颗树);

(2)查询:询问某2个点是否在同一个集合中(查询);(3)其他:计算共有几个集合(几棵树);

2、并查集的实现方法(1)举例说明

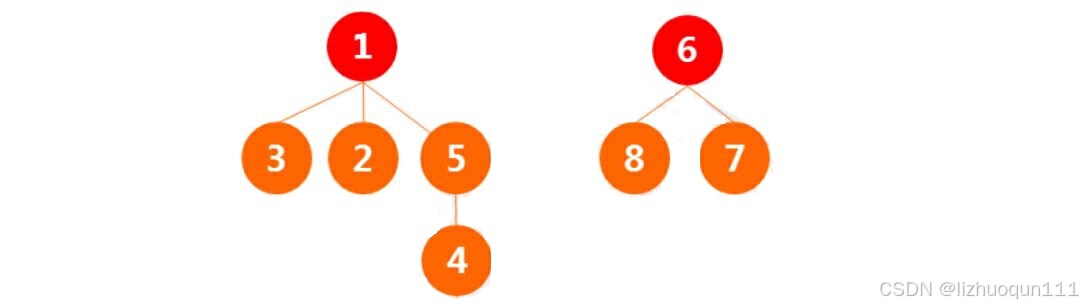
假设有如下8个点:12345678，假设如下两两的结点在一个集合中，通过并查集构建过程的模拟来看最终有几个集合，并理解并查集的构建过程和查询过程。

两两在一个集合中的结点有:

(2)数据结构的实现

实际操作时，我们会使用一个点来代表整个集合，即一个元素的根结点(可以理解为父亲)。

实现方法

我们建立一个数组fa[]表示一个并查集，fa[i]表示i的父节点。

(1)初始化:每一个点都是一个集合，因此自己的父节点就是自己fa[i]=i

(2)查询:每一个节点不断寻找自己的父节点，若此时自己的父节点就是自己，那么该点为集合的根结点，返回该点。

(3)合并;合并两个集合只需要合并两个集合的根结点，即fa[RootA]=RootB，其中RootA,RootB是两个元素的根结点。

(4)路径压缩:

大多数情况下，在查询过程中只关心根结点是什么，并不关心这棵树的形态。因此我们可以在查询操作的时候将访问过的每个点都指向树根，这样的方法叫做路径压缩。

初始化模板:

for(int i=1;i<=n;i++) f[i]=i;

基本查询模板:求x的根

int find(int x){

return f[x]== x?x:find(f[x]);

}

路径压缩查询模板:

f[x]==x?x:f[x]=find(f[x])

合并模板:先判断x和y是否在同一个集合

//集合合并

void merge(int x,int y){

int fx = find(x);

int fy = find(y);

if(fx!= fy)f[fx] = fy;

}

是不是亲戚

题目描述

若某个家族人员过于庞大，要判断两个是否是亲戚，确实还很不容易，现在给出某个亲戚关系图，求任意给出的两个人是否具有亲戚关系。

规定：x和y是亲戚，y和z是亲戚，那么x和z也是亲戚。如果x,y是亲戚，那么x的亲戚都是y的亲戚，y的亲戚也都是x的亲戚。

输入

第一行：三个整数n,m,p，（n<=5000,m<=5000,p<=5000），分别表示有n个人，m个亲戚关系，询问p对亲戚关系。

以下m行：每行两个数Mi，Mj，1<=Mi，Mj<=N，表示Mi和Mj具有亲戚关系。

接下来p行：每行两个数Pi，Pj，询问Pi和Pj是否具有亲戚关系。

输出

P行，每行一个'Yes'或'No'。表示第i个询问的答案为“具有”或“不具有”亲戚关系。

样例

输入

6 5 3

1 2

1 5

3 4

5 2

1 3

1 4

2 3

5 6

输出

Yes

Yes

No

#include<bits/stdc++.h>

using namespace std;

const intN=5010;

int fa[N];//存储每个元素的父

int n,m,q;

//2查询:查找元素x的根

int find(int x){

//如果某元素的父是自己，找到了根

//如果不是就继续找其父的根

if(fa[x] ==x) return x;

else return fa[x]=find(fa[x]);

//路径压缩:找到x的根之后，让x的父直接指向x的根

}

//3.合并函数:将x和v合并到一个集合前提:x和y不在一个集合，才能合并

void merge(int x,int y){

int fx=find(x);

//找x的根

int fy=find(y);

//如果根不同，说明不在一个集合

if(fx!= fy){

fa[fx] =fy;

}

}

int main(){

cin>>n>>m>>q;

//1.初始化fa，让每个元素的父指向自己，也就是初始状态每个元素是一个独立的集合           for(int i =1;i <= n;i++){

fa[i] =i;

}

//读入m对关系

int x,y;

for(int i = 1;i <= m;i++){

cin>>x>>y;

merge(x,y);//合并

}

//读入q次查询

for(int i =1;i <= q;i++){

cin>>x>>y;

//如果x和y根相同，说明在一个集合

if(find(x)== find(y)){

cout<<"Yes"<<endl;

}else{

cout<<"No"<<endl;

}

return0;

}

修路

题目描述

某市调查城镇交通状况，得到现有城镇道路统计表。表中列出了每条道路直接连通的城镇。市政府 "村村通工程" 的目标是使全市任何两个城镇间都可以实现交通（但不一定有直接的道路相连，只要相互之间可达即可）。请你计算出最少还需要建设多少条道路？

输入

输入包含若干组测试数据，每组测试数据的第一行给出两个用空格隔开的正整数，分别是城镇数目n和道路数目m（输入n=0表示测试数据结束）；随后的m行对应m条道路，每行给出一对用空格隔开的正整数，分别是该条道路直接相连的两个城镇的编号。简单起见，城镇从1到n编号。

注意：两个城市间可以有多条道路相通。

对于 100% 的数据，保证 1≤n<1000 。

输出

对于每组数据，对应一行一个整数。表示最少还需要建设的道路数目。

样例

输入

4 2

1 3

4 3

3 3

1 2

1 3

2 3

5 2

1 2

3 5

999 0

0

输出

1

0

2

998

#include <bits/stdc++.h>

using namespace std;

/*

本题求解的关键点:

求出有几个集合，修道路的最少数量=集合数量-1

求有几个集合:求有几个根(f[i]==i)

*/

int fa[1010];

 int n,m,c;

//查询

int find(int x){

if(x==fa[x]) return x;

else return fa[x]=find(fa[x]);

}

//合并

void merge(int x,int y){

int fx=find(x);

int fy=find(y);

if(fx!= fy){

fa[fx] =fy;

}

}

int main(){

//读入，指导n=0

while(true){

cin>>n;//n个城镇

if(n== 0) break;

cin>>m;//m条道路

//初始化fa数组

for(int i =1;i<= n;i++) fa[i] =i;

//读入m条道路

int x,y;

for(int i=1;i <= m;i++){

cin>>x>>y;

merge(x,y);

}

//计算有多少个集合(有多少个根)

c= 0;

//计算n个点中，有几个根

for(int i =1;i <= n;i++){

if(fa[i] == i) c++;

}

cout<<c -1<<endl;

}

return 0;

}

躲避拥堵的最佳路线

题目描述

小明所在的城镇有m条路连接了n个区（n个区的编号在1~n的范围内），每条大道将两个区相连接，每条大道有一个拥挤度。小明想要开车从s区去t区，请你帮他规划一条路线，使得经过道路的拥挤度的最大值最小。

输入

第一行有四个用空格隔开的n，m，s，t，其含义见题目描述。

接下来m行，每行三个整数u,v,w，表示有一条大道连接区u和区v，且拥挤度为w，道路为双向道路，两个方向都可以走。

两个区之间可能存在多条大道。

数据规模与约定
对于 30% 的数据，保证n≤10。
对于 60% 的数据，保证n≤100。
对于 100% 的数据，保证1≤n≤10^4，1≤m≤2×10^4, w≤10^4,1≤s,t≤n。且从 s 出发一定能到达 t 区。

输出

输出一行一个整数，代表最大的拥挤度。

样例

输入

3 3 1 3

1 2 2

2 3 1

1 3 3

输出

2

看到求最大值的最小判断要用二分解决。我们可以二分这个拥挤度，在判断这个拥挤度是否可行时，把所有拥挤度大于mid的边都去掉，最后并查集判断s点与t点是否联通即可。

#include <bits/stdc++.h>

using namespace std;

/*

经过道路的拥挤度的最大值最小(二分答案)

解题思路:

1二分最大拥挤度，1=min(拥挤度)，r=max(拥挤度)

2.check(mid):检验如果最大拥挤度为mid，能否从s区到t区

检验方法:

1. 将所有道路中，拥挤度值<=mid的道路修起来(合并)

(2)查询s和t是否在一个集合

3.求二分的左边界

*/

int n,m,s,t;

int fa[10010];

int l = INT_MAX,r = INT_MIN,mid;

//存储从x区到y区有道路，道路的拥挤度为

struct city{

int x,y,len;

};

city a[20010];

//查询

int find(int x){

if(x==fa[x]) return x;

else return fa[x]=find(fa[x]);

}

//合并

void merge(int x,int y){

int fx= find(x);

int fy=find(y);

if(fx != fy) fa[fx]=fy;

}

//检验:如果最大拥挤度为mid，能否从s区到t区

bool check(int mid){

//初始化

for(inti=1;i <= n;i++){

fa[i] =i;

}

//将所有道路中拥挤度的值<=mid的道路修起来(合并道路相连的区)

for(int i=1;i <= m;i++){

if(a[i].len<= mid){

merge(a[i].x,a[i]·y);

}

}

//判断s能否去 t:如果在一个集合就能去

return find(s)== find(t);

}

int main(){

cin>>n>>m>>s>>t;

//读入m条道路的数据

for(int i =1;i <= m;i++){

cin>>a[i].x>>a[i].y>>a[i].len;

//求拥挤度的最大最小值作为二分的边界

l=min(l,a[i].len);

r=max(r,a[i].len);

}

//二分答案

while(l<= r){

//mid=l+r>>1;

mid=(l+r)/2;

//检验如果最大拥挤度为mid，能从s区到t区

if(check(mid)) r=mid-1;

 else l=mid +1;

}

//表示拥挤度最大值的最小

cout<<l;

 return 0;

}

团队数量

题目描述

芝加哥组织了一场激烈的军事竞赛，很多国家的军人慕名而来，他们要么是队友，要么是敌人。

现建立如下规则：

我的队友的队友，是我的队友；

我的敌人的敌人也是我的队友；

两个人只要是队友，就认为他们属于同一团队，现给你若干参赛军人之间的关系，请问：最多有多少个团队？

输入

第一行是一个整数N(2<=N<=1000)，表示参赛的人数（从1编号到N）。 第二行M(1<=M<=5000)，表示关于参赛者的关系信息的条数。 以下M行，每行可能是F p q或是E p q（1<=p q<=N），F表示p和q是队友，E表示p和q是敌人。输入数据保证不会产生信息的矛盾。

输出

输出文件只有一行，表示最大可能的团队数。

样例

输入

6

4

E 1 4

F 3 5

F 4 6

E 1 2

输出

3

说明

样例结束：[3,5]是一个团队，[4,6]是一个团队，由于1和4、1和2都是敌人，2和4自然成为队友，因此[2,4,6]成为团队，1单独为1个团队，最终有3个团队。

种类并查集;普通的并查集维护的是具有连通性、传递性的关系，例如亲戚的亲戚是亲戚。

种类并查集是在此基础上再进行一些“分类”，类似“敌人的敌人是朋友”的分类。

1、种类并查集常规思路:扩大并查集规模。

2、比如:要维护朋友和敌人这两个关系，则将普通并查集的规模扩大两倍，原来的1~n

还是存放朋友关系，但是n+1~2n则是存放敌人关系，然后每次操作都分别维护。

1. 种类并查集加强版:上面举的例子是针对两种对立关系，但是有些题目会涉及三种循环关系，怎么做呢?其实就是将扩大两倍规模变为扩大三倍规模。

题目的两种关系已经说得很明确了，我们将朋友关系的两个人合并。对于是敌人关系的两个人，由于敌人的敌人是我的朋友，所以我们可以建立一个自己虚拟的敌人(比如:认为 x和x+n是敌人，那么如果x和v是敌人的话，v和x+n就是朋友)再与对方形成朋友关系。

三目运算符:判断表达式?值 1:值 2;

如果表达式成立，获得值1，否则获得值2;

例子:

int a=1,b=2;

cout<<(a > b?a:b);

#include<bits/stdc++.h>

using namespace std;

Int f[2010];//表示关系

int n,m;

//查询

int find(int x){

// if(x==f[x]) return x;

// else return f[x]=find(f[x]);

return x==f[x]?x:f[x]=find(f[x]);

}

//合并

void merge(int x,int y){

int fx= find(x);

int fy= find(y);

if(fx!= fy) f[fx]=fy;

}

int main(){

cin>>n>>m;

//初始化f数组

for(int i =1;i <= 2 * n;i++){

f[i]=i;

}

//读入关系

char c; int x,y;

for(int i =1;i <= m;i++){

cin>>c>>x>>y;

if(c=='F') merge(x,y);

 else{

merge(y+n,x);

merge(x+n,y);

}

}

//求有几个根

int r = 0;

for(int i=1;i <= n;i++){

if(f[i] == i) r++;

}

cout<<r;

return 0;

}

观押罪犯

题目描述

S城现有两座监狱，一共关押着N名罪犯，编号分别为1−N。他们之间的关系自然也极不和谐。很多罪犯之间甚至积怨已久，如果客观条件具备则随时可能爆发冲突。我们用“怨气值”（一个正整数值）来表示某两名罪犯之间的仇恨程度，怨气值越大，则这两名罪犯之间的积怨越多。如果两名怨气值为c的罪犯被关押在同一监狱，他们俩之间会发生摩擦，并造成影响力为c的冲突事件。

每年年末，警察局会将本年内监狱中的所有冲突事件按影响力从大到小排成一个列表，然后上报到S城Z市长那里。公务繁忙的Z市长只会去看列表中的第一个事件的影响力，如果影响很坏，他就会考虑撤换警察局长。

在详细考察了N名罪犯间的矛盾关系后，警察局长觉得压力巨大。他准备将罪犯们在两座监狱内重新分配，以求产生的冲突事件影响力都较小，从而保住自己的乌纱帽。假设只要处于同一监狱内的某两个罪犯间有仇恨，那么他们一定会在每年的某个时候发生摩擦。

那么，应如何分配罪犯，才能使 Z 市长看到的那个冲突事件的影响力最小？这个最小值是多少？

输入

输入数据的每行中两个数之间用一个空格隔开。

第一行为两个正整数N和M，分别表示罪犯的数目以及存在仇恨的罪犯对数。

接下来的M行每行为三个正整数aj，bj，cj，表示aj号和bj号罪犯之间存在仇恨，其怨气值为cj。

数据保证1<=aj<=bj<=N,0<=cj<=109,且每对罪犯组合只出现一次。

【数据范围】
对于30%的数据有N≤15。
对于70%的数据有N≤2000，M≤50000。
对于100%的数据有N≤20000，M≤100000。

输出

输出数据共1行，为Z市长看到的那个冲突事件的影响力。如果本年内监狱中未发生任何冲突事件，请输出0。

样例

输入

4 6

1 4 2534

2 3 3512

1 2 28351

1 3 6618

2 4 1805

3 4 12884

输出

3512

说明

【输入输出样例说明】罪犯之间的怨气值如下面左图所示，右图所示为罪犯的分配方法，市长看到的冲突事件影响力是3512（由2号和3号罪犯引发）。其他任何分法都不会比这个分法更优。

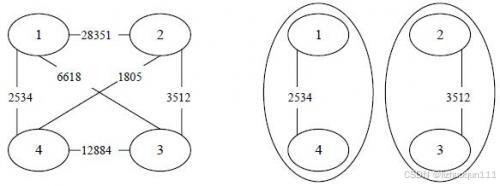
要尽可能大的将危害大的罪犯放到两个集合，那么将怨气值降序排序，逐个讨论每对罪犯，如果发现有两对罪犯在一个集合，那么计算结束，输出这个怨气值。如果不在一个集合，那么该罪犯要和对方的敌人在一个集合，对方的敌人要和该罪犯在一个集合。

#include<bits/stdc++.h>

using namespace std;

/*

1.将怨气值大的罪犯，尽可能拆到不同的监狱

2.维护种类并查集

将每个人和其敌人的敌人合并到一个集合 x，y+n 合并，y，x+n 合并

1. 直到出现第一组两个人已经在一个监狱的情况此时的怨气值就是最大的怨气值

*/

int f[40010];

int n,m;

//x和y是敌人，怨气值为v

struct node{

int x,y,v;

};

node a[100010];

//按怨气值降序

bool cmp(node n1，node n2){

return n1.v>n2.v;

}

//查询

int find(int x){

return x==f[x]?x:f[x]=find(f[x]);

}

//合并

void merge(int x,int y){

int fx = find(x);

int fy=find(y);

if(fx!= fy) f[fx] = fy;

}

int main(){

cin>>n>>m;//读入关系

for(int i =1;i <= m;i++){

cin>>a[i].x>>a[i].y>>a[i].v;

}

//将怨气值降序排序，从最大的开始拆分

sort(a+1,a+m+1,cmp);

//初始化

for(int i=1;i <= n * 2;i++){

f[i]=i;

}

//处理关系

for(int i =1;i <= m;i++){

//如果发现2个人已经在一座监狱，必定有冲突

if(find(a[i].x)== find(a[i]·y)){

cout<<a[i].v;

return 0;

}else{

//将每个人和其假想的好友合并

merge(a[i].x+n,a[i]·y);

merge(a[i]·y+n,a[i].x);

}

cout<<0;

return 0;

}

二、并查集的应用一-最小生成树

在含有n个顶点的连通网中选择n-1条边，构成一棵极小连通子图，并使该连通子图中 n-1 条边上权值之和达到最小，则称其为连通网的最小生成树。例如，对于如右图所示的连通网可以有多棵权值总和不相同的生成树。

应用场景:

例如:要在n个城市之间建设道路，主要目标是要使这n个城市的任意两个之间都可

以通行，但建设道路的费用很高，且各个城市之间建设道路的费用不同，因此另一个目标是

要使建设道路的总费用最低。这就需要找到带权的最小生成树。

Kruskal算法

基本思想:按照权值从小到大的顺序选择 n-1 条边，并保证这 n-1 条边不构成回路。

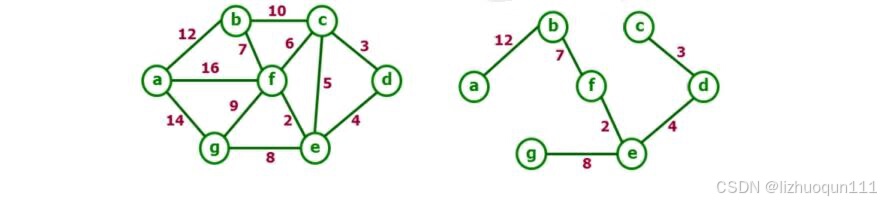
具体做法:首先构造一个只含n个顶点的森林，然后依权值从小到大从连通网中选择边

加入到森林中，并使森林中不产生回路，直至森林变成一棵树为止。

最短网络 Agri-Net（USACO3.1）

题目描述

Farmer John 被选为他们镇的镇长！他其中一个竞选承诺就是在镇上建立起互联网，并连接到所有的农场。当然，他需要你的帮助。

FJ 已经给他的农场安排了一条高速的网络线路，他想把这条线路共享给其他农场。为了用最小的消费，他想铺设最短的光纤去连接所有的农场。

你将得到一份各农场之间连接费用的列表，你必须找出能连接所有农场并所用光纤最短的方案。每两个农场间的距离不会超过 10^5。

输入

第一行农场的个数N（3≤N≤100）。
接下来是一个N×N 的矩阵，表示每个农场之间的距离。理论上，他们是N行，每行由N个用空格分隔的数组成，实际上，由于每行80个字符的限制，因此，某些行会紧接着另一些行。当然，对角线将会是0，因为不会有线路从第i个农场到它本身。

输出

只有一个输出，其中包含连接到每个农场的光纤的最小长度。

样例

输入

4

0 4 9 21

4 0 8 17

9 8 0 16

21 17 16 0

输出

28

最小生成树:克鲁斯卡尔(Kruskal)算法，基本思想:按照权值从小到大的顺序选择n-1条边，并保证这n-1条边不构成回路。

具体做法;首先构造一个只含n个顶点的森林，然后依权值从小到大从连通网中选择边加入到森林中，并使森林中不产生回路，直至森林变成一棵树为止。

#include <bits/stdc++.h>

using namespace std;

/*

1.读入数据，将数据存入结构体数组;

2.对结构体数组按照建网络的长度，从小到大排序;

3.选出n-1条边，不能构成回路，长度的和就是最小长度;*/

int f[110];

//存储x到y号农场修网络需要长度为len的光纤

struct node{

int x,y,len;

};

node a[6000];

Int n,t,k=0;//k表示数组下标

//排序比较

bool cmp(node n1,node n2){

return n1.len<n2.len;}

//查询

int find(int x){

returnx==f[x]?x:f[x]=find(f[x]);

}

int main(){

cin>>n;

//读入数据，存入结构体数组

for(int i=1;i <= n;i++){

for(int j=1;j<= n;j++){

cin>>t;

if(i < j){

k++;

a[k].x=i;

a[k]·y=j;

a[k].len=t;

}

}

}

//排序

sort(a+1,a+k+1,cmp);

//初始化

for(int i=1;i <= n;i++){

f[i]=i;

}

//从所有的路线中选出n-1条路线

Int s=0;//最短路径的和

Int c=0;//修了几条路

for(int i = 1;i <= k;i++){

//如果两个点之间本身没有路，就可以修//否则不能修，会构成回路

int fx=find(a[i].x);

int fy=find(a[i].y);

if(fx!= fy){

f[fx] = fy;

 c++;

s=s+a[i].len;

}

//如果修路的数量足够了(n-1条)

if(c== n-1){

cout<<s;

break;

}

}

return 0;

}

三、带权并查集

带权并查集是结点存有权值信息的并查集。相比于一般的并查集，带权并查集需要开辟两个数组:一个是f[N]，用来判断集合关系;一个是value[N]，用来描述其与根节点的关系。

当两个元素之间的关系可以量化，并且关系可以合并时，可以使用带权并查集来维护元

素之间的关系。

带权并查集每个元素的权值通常描述其与并查集中祖先的关系，这种关系如何合并，路径压缩时就如何压缩。

基于路径压缩，带权并查集:

它的每一条边都记录了每个节点到根节点的一个权值，这个权值该设为什么由具体的问

题而定，一般都是两个节点之间的某一种相对的关系，但是考虑到权值就会有两个问题:

1.每个节点都记录的是与根节点之间的权值，那么在 find的路径压缩过程中，权值也

应该做相应的更新，因为在路径压缩之前，每个节点都是与其父节点链接着，value 自然也

是与其父节点之间的权值;

1. 在两个并查集做合并的时候,权值也要做相应的更新,因为两个并查集的根节点不同。

模板代码:

int find(int x){

if(f[x]==x) return x;

 else{

//更新路径的值

Int t=f[x];//记录当前父节点的编号

f[x]=find(f[x]);//路径压缩

dis[x]=dis[x]+dis[t];//回溯时，更新权值

return f[x];

}

}

可以看到更新权值只多了两行代码，先记录下原本父节点的编号，因为在路径压缩后父节点就变为根节点了，再将当前节点的权值加上原本父节点的权值，此时父节点的权值已经是父节点到根节点的权值了，因此加上这个权值就会得到当前节点到根节点的权值。

立方体积木Cube Stacking

题目描述

约翰和贝茜在玩一个方块游戏。编号为1…n的n(1≤n≤30000)个方块正放在地上，每个构成一个立方柱。
游戏开始后，约翰会给贝茜发出P(1≤P≤100000)个指令。指令有两种：
移动（M）：将包含 X 的立方柱移动到包含 Y 的立方柱上。
统计（C）：统计含 X 的立方柱中，在 X 下方的方块数目。
写个程序帮贝茜完成游戏。

输入

第1行输入P，之后P行每行输入一条指令，形式为 M X Y 或者 C X。
输入保证不会有将立方柱放在自己头上的指令。

输出

输出共P行，对于每个统计指令，输出其结果。

样例

输入

6

M 1 6

C 1

M 2 4

M 2 6

C 3

C 4

输出

1

0

2

#include<bits/stdc++.h>

using namespace std;

const int N=30010;

intf[N];//表示关系

int dis[N];//表示每个元素离根的距离

int len[N];//表示第i列有几个立方块

int p;//查询

int find(int x){

if(f[x] == x) return x;

else{

Int t=f[x];//记录当前父节点的编号

f[x]=find(f[x]);//递归找根

//回溯的时候，更新 dis的值

dis[x] =dis[x] +dis[t];

//cout<<x<<",parent:"<<f[x]<<",dis:"<<dis[x]<<endl;

return f[x];

}

}

//合并

void merge(int x,int y){

int fx=find(x);

int fy=find(y);

if(fx!= fy){

f[fx]=fy;//更新dis

dis[fx]=dis[fx]+len[fy];//更新该列中方块的数量

len[fy]=len[fy] +len[fx];

len[fx] = 0;

}

}

int main() {

cin>>p;

//初始化

for(int i =1;i <= 30000;i++){

f[i]=i;

len[i]=1;//默认每一列有1个元素

}

//读入指令

char c;

int x,y;

for(int i =1;i <= p;i++){

cin>>c>>x;

//如果是查询

if(c == 'C'){

find(x);//更新dis的值，做路径压缩

cout<<dis[x]<<endl;

}else{

//移动

cin>>y;

merge(x,y);

}

return 0;

}