小白都能看懂的Transformer详解和形象化解释

Transformer已经大火了很久了，但是一直也没有机会详细学习一下，刚好最近需要用到Transformer，借此机会详细学习一下吧！以下是我在各个地方学到的知识综合的笔记，主要是方便自己以后阅读，个人觉得挺详细的，希望在我记笔记的同时也能帮到大家。

什么是Transformer？

Transformer网络提出于2017年，它处理的任务类型是和RNN所擅长的内容相似的序列信息，但是Transformer却更快更强。短短三年间依托于这个网络模型诞生了非常多的强大算法，这些算法是如此强大，以至于这个模型和大规模预训练的潮流一起让很多人第一次开始想象思考通用人工智能的到来。

Transformer类似一个CNN，可以在同一时间计算所有输入单词，并得到这些单词各自的表征向量。重要的是，这一次性的处理中得到的每一个表征向量都是在考虑到整句话语境信息以后的结果！这使得Transformer不再需要像RNN一样按照序列顺序处理信息，一来解决了长期依赖问题，而来也使得训练速度加快。

而这一切的基础正是Self-Attention。接下来我们就将从Self-Attention机制开始，详细的介绍如何构建一个transformer网络。

Self-Attention机制讲解

在这一部分，将以总分的形式介绍Attention机制，先介绍核心机制，再依次讲解各个步骤。耐心跟着看下去，相信你一定能懂！

Attention机制核心公式

注意力Attention机制的最核心的公式为：

这个公式中的Q、K和V分别代表Query、Key和Value。在这个公式中涉及到了向量点乘，因此我们从向量点乘开始看起。

向量点乘

首先复习一下向量点乘的概念，对于两个行向量X和Y，其中：
$$\begin{gathered} X=[x0,x1,x2,x3,\dots \dots ,xn] \\ Y=[y0,y1,y2,y3,\dots \dots ,yn] \\ X\cdot Y=x0y0+x1y1+\dots \dots +xnyn \end{gathered}$$

向量点乘的几何意义是：向量 X 在向量 Y 方向上的投影再与向量 Y 的乘积，能够反应两个向量的相似度。向量点乘结果大，两个向量越相似。

Attention机制中的Q、K、V从何而来？

在上述Attention核心机制中，我们看到Attention的关键就是对Q、K、V进行一系列的计算，那么这三个字母到底表示什么呢？他们的数据又是从何而来呢？

接着看：
$Q、K、V$其实都是基于输入矩阵$X$线性变换而来的。用公式表示则是：
$$\begin{gathered} Q=X{W}^Q \\ K=X{W}^K \\ V=X{W}^V \end{gathered}$$

用图片表示就是：

其中，$W^Q，W^K和W^V$是三个可训练的参数矩阵。输入矩阵 $X$分别与$W^Q，W^K和W^V$相乘，生成矩阵$Q、K$和$V$，相当于经历了一次线性变换。

为什么Attention不直接使用X呢？
因为使用经过矩阵乘法生成的这三个可训练的参数矩阵，可增强模型的拟合能力。

上述介绍可能有点空洞，不容易理解，下面通过实际例子讲解一下上述过程：
假设现在输入‘Thinking Machine’，共两个单词。
首先，我们需要将Thinking 和Machine进行Embedding词向量转化，假设每个单词转化为一个由4个数值表示的行向量。此时$X$矩阵的维度为（2，4）。

接下来，我们随机初始化三个维度为（4，3）的参数矩阵$W^Q，W^K和W^V$，用于生成矩阵$Q、K、V$。

则，矩阵$Q、K、V$的计算过程如下：

这一步得到了对应的$Q、K$和$V$。这三个矩阵的维度为（2，3）。
其中，每个矩阵的第一行分别对应单词thinking的查询向量$q1$、键向量$k1$和值向量$v1$。第二行分别对应单词machine的查询向量$q2$、键向量$k2$和值向量$v2$。

也就是说，每个单词分别有自己对应的三个向量：$qi$、$ki$和$vi$

此时，我们已经得到了三个矩阵$Q、K、V$，那么，接下来做什么呢？

得到$Q、K、V$后该怎么办？

计算自注意力的第一步：计算$Q、K、V$，上述已经实现。
计算自注意力的第二步：计算得分。
第三步和第四步：将分数除以8并Softmax
第五步：将每个值向量乘以softmax分数
第六步：对加权值向量求和

即，得到矩阵$Q、K、V$后，我们首先该计算相应得分。

那么问题来了，什么是得分呢？怎么获得得分呢？
请带着问题继续往下看：

假设我们以输入的第一个词“Thinking”为例，我们需要做的是：拿输入句子中的每个单词（也就是Thinking和Machine）对“Thinking”进行打分。

这些分数是通过输入句子的所有单词的键向量（$k1、k2$）与“Thinking”的查询向量（$q1$）点积来计算的。具体步骤如下：

这里便对应了Attention核心机制中的 $Q{K}^T$，这里相当于两个向量进行点乘，结果是一个具体的数值，表示两个向量的相似程度。

接下来：
第三步和第四步：将分数除以8并Softmax
注意，这里的8是论文中使用的键向量的维数64的平方根，这会让梯度更稳定。这里也可以使用其它值，8只是默认值，这样做是为了防止内积过大。然后通过softmax传递结果。softmax的作用是使所有单词的分数归一化，得到的分数都是正值且和为1。

这个softmax分数决定了每个单词对编码当下位置（“Thinking”）的贡献。

接下来：
第五步：将每个值向量乘以softmax分数
即$0.88\ast v1$， $0.12\ast v2$
这是为了准备之后将它们求和。这里的直觉是希望关注语义上相关的单词，并弱化不相关的单词(例如，让它们乘以0.001这样的小数)。

接下来：
第六步：对加权值向量求和，然后即得到自注意力层在该位置的输出$z1$ (在我们的例子中是对于第一个单词)。

即$0.88\ast v1+0.12\ast v2=z1$，最终结果是一个与$v1$维度相同的向量$z1$。

整体的计算图如图所示（下图包含了两个单词的计算Thinking和Machine）：

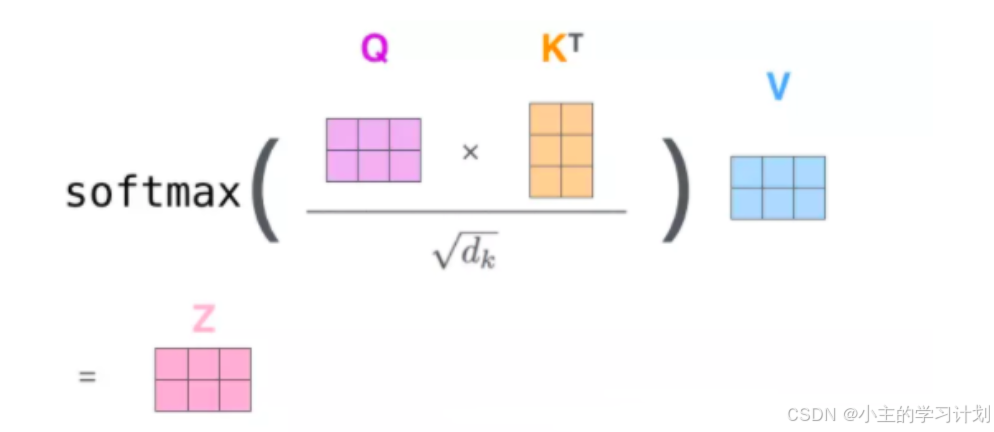
Self-Attention核心流程概括

上面讲了那么多，可能看到这里对Attention的具体流程还是有点模糊，接下来我将再举一个具体例子介绍Attention的整体流程：
(这里图片摘自文章Attention机制详解)

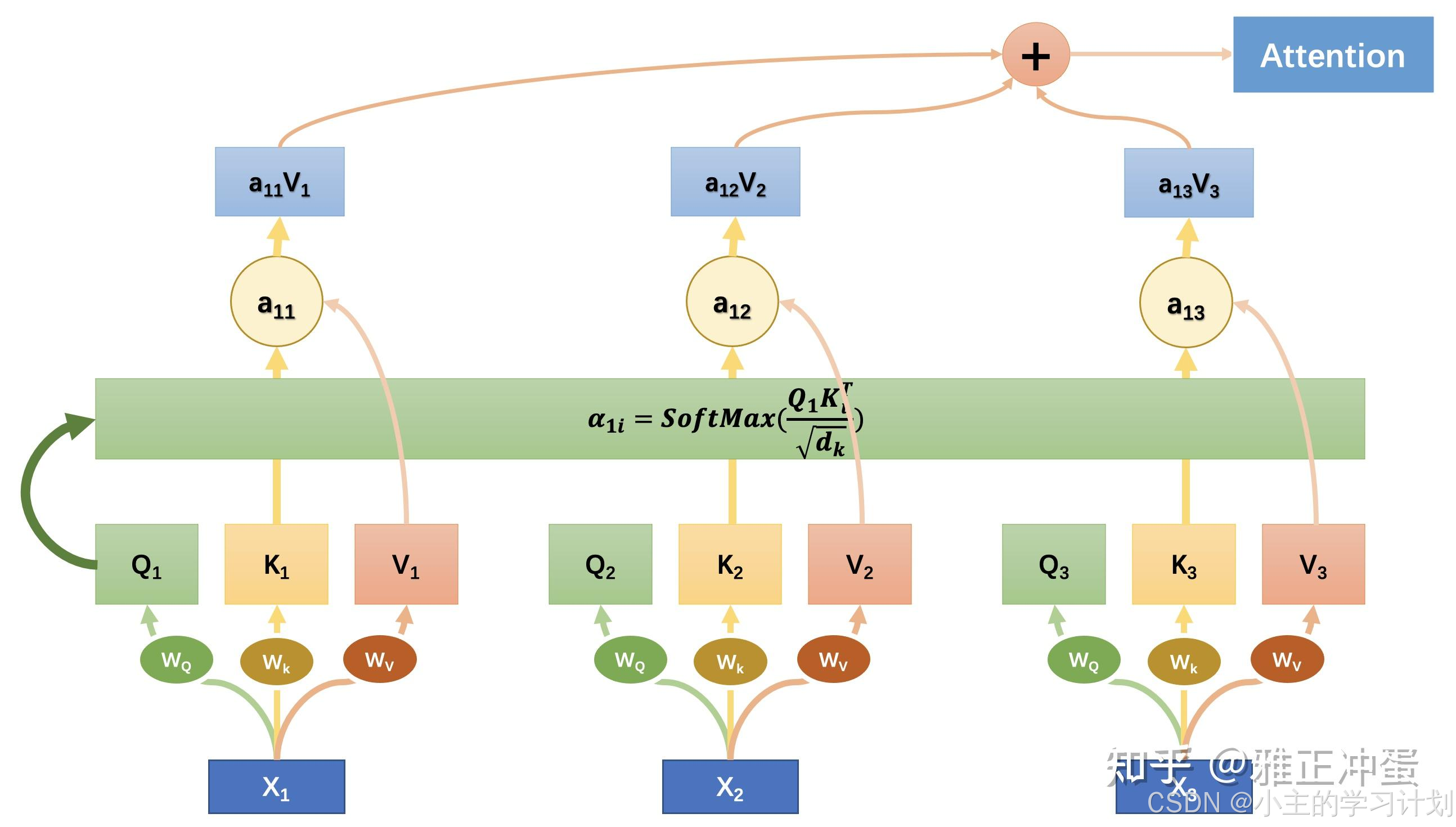
在上图中，输入的是一个句子$W$，这个句子由三个单词组成，分别是$x_1，x_2$，和$x_3$。

1. 首先对每个单词$x_i$进行词向量转化，转化后的每个$x_i$为一个$n$维的行向量。

2. 用三个矩阵$W_Q,W_K,W_V$分别乘以每个词向量$x_i$，得到三组表征$Q_i,K_i,V_i$，其中，$Q_i=x_i{W}_Q,K_i=x_i{W}_K,V_i=x_i{W}_V$

3. 接下来我们分别对三个词计算全局对齐权重，这张图中只演示计算了$x_1$ 眼中其他词的权重：
   首先我们取出 $x_1$的查询 $Q_1$，对所有的其他$K$计算，其中$\sqrt{d_k}$代表Key的长度， $e_{ij},{\alpha }_{ij}$都是标量:
   
   其中${\alpha }_{ij}$代表了在第 $i$个单词的眼中，应该给第$j$个单词分配多少权重。
   $1/\sqrt{d_k}$把计算出来的分数缩小一定倍数，防止SoftMax产生的梯度过小。

4. 最后我们把所有单词对应的$V_j$按照权重${\alpha }_{ij}$求和，就得到了第$i$个单词的Attention值$A_i$了。
   

多头（Multi-Head）Attention机制

前面我们详细介绍了self-Attention机制的整个流程，然而在Transformer中主要用到的是多头Attention机制，因此，接下来我将详细介绍多头Attention的流程：

下图精彩地展示了Multi-Head Attention的计算过程：
（这里图片摘自文章Transformer详解）

如上图我们现在有了不只一层的Attention层（上图共展示了三层，也就是三头注意力机制）。

注意，上面这张图只展示了第一个词语$X_1$在三个不同的head中对应的输出，我们还需要把这个模型在其他词语（$X_2,X_3,\dots \dots$）上都运行一遍，才能得到最终输出。

单看上图其实并不明了，接下来我们用文字详细描述一下多头注意力机制的全部过程，请耐心看完哦，相信你一定能看懂！

1. 首先，假设我们现在有一个句子有 $T$ 个单词。
2. 我们把每个单词带入词嵌入模型，计算出每个单词对应的词向量 $x_i$ ，假设得到的每个词向量的维度为 $[1,512]$。即每个单词被表示为一个行向量，该行向量由512个数值组成。
3. 接下来，我们把所有词向量叠在一起得到一个句子矩阵 $X$ ，则矩阵 $X$ 的大小就是 $[T,512]$。矩阵中的每一行表示句子中的一个单词。
4. 重点来了！！！接下来，我们开始计算第一层注意力。
   假设第一层的三个参数矩阵为$W_1^Q,W_1^K,W_1^V\in R^{[512,64]}$，这三个参数矩阵用来构造第一层所有的$Q,K,V$。
   ①构造查询矩阵 $Q$：$Q=X{W}_1^Q$，则矩阵 $Q$ 的维度为$[T,64]$。在矩阵 $Q$ 中，每一行 $q_t\in R^{[1,64]}$ 表示第 $t$ 个单词对应的查询Query。
   ②构造矩阵 $K$：$K=X{W}_1^K$，则矩阵 $K$ 的维度为$[T,64]$。在矩阵 $K$ 中，每一行 $k_t\in R^{[1,64]}$ 表示第 $t$ 个单词对应的Key。
   ③构造矩阵 $V$：$V=X{W}_1^V$，则矩阵 $V$ 的维度为$[T,64]$。在矩阵 $V$ 中，每一行 $v_t\in R^{[1,64]}$ 表示第 $t$ 个单词对应的Value。
   ④接下来，基于上述矩阵$Q、K、V$构造对齐权重${\alpha }_1$ ，${\alpha }_1=Softmax(\frac{Q_1{K}_1^T}{\sqrt{d_k}})$，由于$Q、K\in R^{[T,64]}$，则${\alpha }_1\in R^{[T,T]}$。
   现在 ${\alpha }_1$ 的第 $t$ 行${\alpha }_1^{<t>}$就代表着在第 $t$ 个词的眼中，所有的词向量的权重应该是怎样的。${\alpha }_1^{<t>}\in R^{[1,T]}$。
   ⑤接下来我们计算$A_1={\alpha }_1{V}_1$，我们就得到了所有的词向量在第一层自注意力中的Attention值。这里，$A\in R^{[T,64]}$，每一行的 $a_t\in R^{[1,64]}$ 表示第 $t$ 个词语对应的注意力值。
5. 接下来，基于参数矩阵$W_2^Q,W_2^K,W_2^V$计算出第二层的注意力矩阵$A_2$，同理依次计算其他层注意力矩阵$A_3,A_4,\dots \dots ,A_8$。
6. 接着，将$A_1$到$A_8$横向堆叠得到矩阵$A\in R[T,512]$，(64*8=512)，其中$A$的每一行 $a_t\in R^{[1,512]}$ 就代表了第 $t$ 个词语对应的所有层的注意力值叠加在一起的结果。

最终我们的模块就是这样的：输入一个大小为$[T,512]$的句子矩阵$X$，输出一个大小相同的注意力矩阵$A$。

构建一个Transformer Encoder层

上述过程距离Transformer里的一个Encoder Layer已经非常接近了，我们还差最后两样东西就可以造出一个Encoder了——残差连接和Layer Norm。

Layer Normalization

考虑到 Transformer 的深度，我们希望能够使用 Batch Normalization 来减少梯度爆炸和梯度消失问题。但是对于循环网络而言（虽然Transformer并不循环），使用一种类似的叫做 Layer Normalization 的方法也可以有效的促进网络学习。 一张图可以很好的解释 Layer Norm 到底 Norm 了啥：

（这里图片摘自文章Transformer详解）

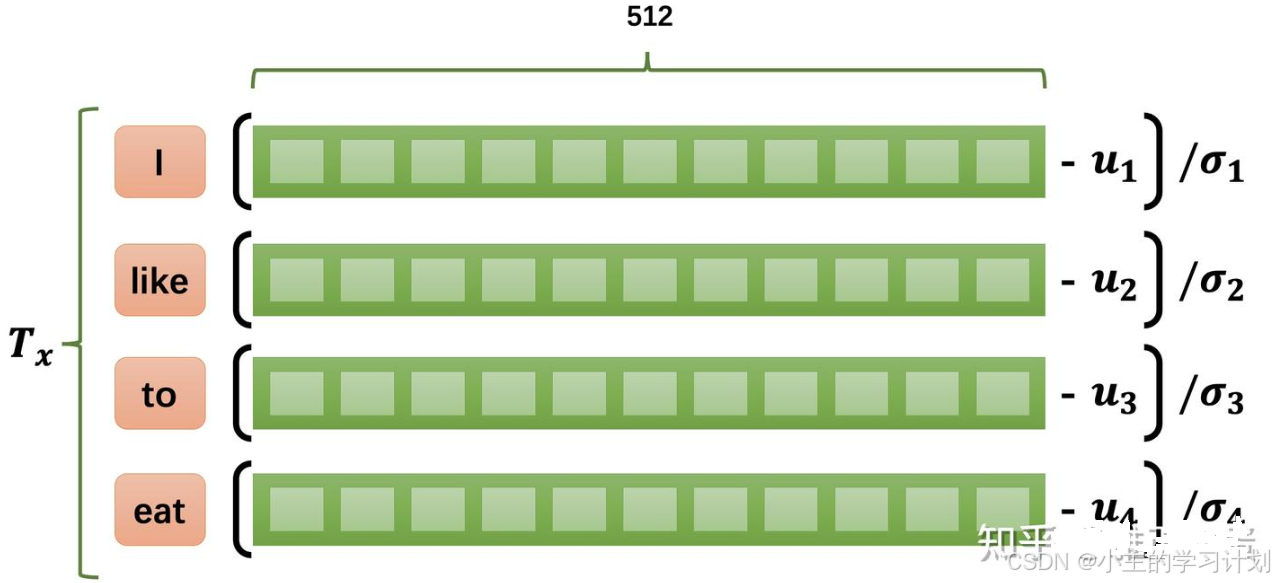
相对于Batch Normalization在mini-batch的不同训练数据之间计算方差和均值，Layer Norm在一个隐藏层的内部的不同值之间进行这个过程。对于层 $l$ ，假设这一层的隐藏单元数为 $H$，则 Layer Normalization 可以描述为：
$${\mu }^l=\frac{1}{H}\sum _{i=1}^H{a}_i^l$$
$${\sigma }^l=\sqrt{\frac{1}{H}\sum _{i=1}^H(a_i^l-{\mu }^l{)}^2}$$
当然，和Batch Normalization一样，我们不能缩放平移一下隐藏层就完事了，我们还得设置两个可学习参数 $g$ 和 $b$ 来允许网络重新设计隐藏层的方差和均值，在一个循环神经网络中，我们的加入了Layer Normalization的隐藏层变换就是下面这样。

而我们在Transformer中对我们的隐藏层 $A\in R^{[T,512]}$，也使用了Layer Normalization，记这一层为LayerNorm(A)：

全连接层

Transformer 中的一个 Encoder 结构可不只一层多头 Attention 层，在从多头Attention 层输出以后，Encoder 模块还要对它进行最后的加工——输入一个全连接层。

这里接着上面多头注意力机制输出的矩阵$A\in R^{[T,512]}$进行：

这个全连接层并不复杂，：
A i [ 1 ] = R e L U ( A i W 1 + b 1 ) = m a x { 0 , A i W 1 + b 1 } A_i^{[1]} = ReLU(A_iW_1+b_1) = max\{0, A_iW_1+b_1\} Ai[1]​=ReLU(Ai​W1​+b1​)=max{0,Ai​W1​+b1​}
在上述公式中，$W\in R^{[512,2048]}$。把每一个$A_i\in R^{[1,512]}$都带入运算得到对应的输出。我们输出的$A_i^{[1]}$的维度为$[T,2048]$。

之后我们再使用一层线性层（不带激活函数）把向量大小变回 $[T,512]$ 即可，因此我们的这个全连接层 $FFN$ 就写作：

F F N ( A ) = m a x { 0 , A i W 1 + b 1 } W 2 + b 2 FFN(A) = max\{0, A_iW_1+b_1\}W_2 + b_2 FFN(A)=max{0,Ai​W1​+b1​}W2​+b2​
其中，$W_2\in R^{[2048,512]}$。

残差链接

由上述介绍可以看出，Encoder模块有两个子模块：Multi-Head Self-Attention层和FFN层。这两个模块之间得到的输出还夹着残差连接和LayerNorm层，一张图很好的表明了这个模块是如何构建的。

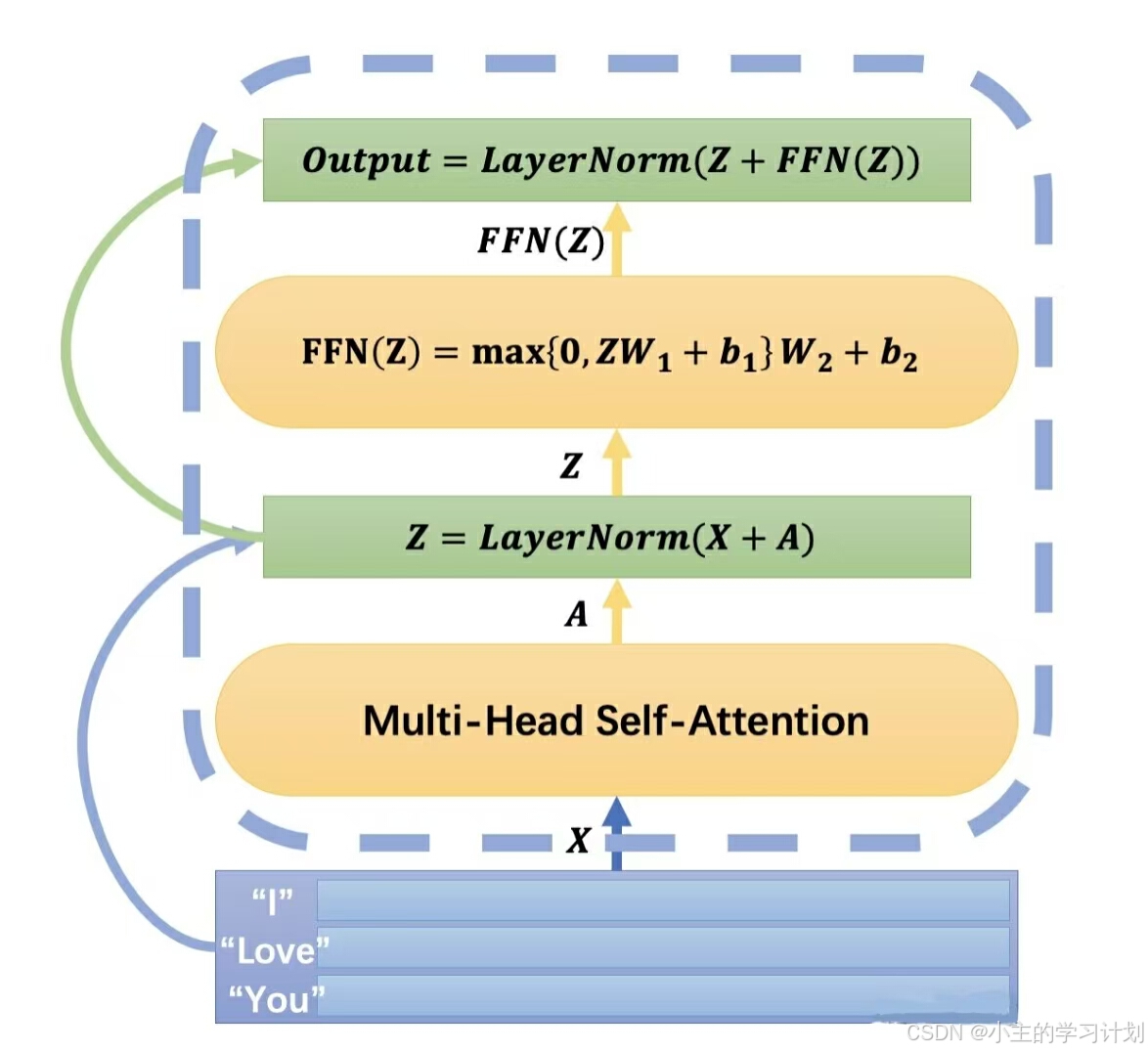
上图中，每个子模块的首位两段都添加了跳层连接和LayerNorm，两个这样的子模块相拼接，就得到了我们的一个Encoder模块。

注意，矩阵$X，A，Z$，以及 $FFN(Z)、Output$大小全都为$[T,512]$。这样的网络我们把它一层叠一层，总共叠加了6层。当然，这六层之间没有任何的参数共享，它们是各自被训练的6层。这6层就共同构成了一个Transformer结构中的Encoder部分，可以很好的解离出文本中的特征和理解文本。接下来我们就要开始设计Transformer的“嘴巴”——Decoder Transformer部分。

构建Decoder Transformer

加入Transformer的Decoder部分以后的整个结构就是下图这样的：

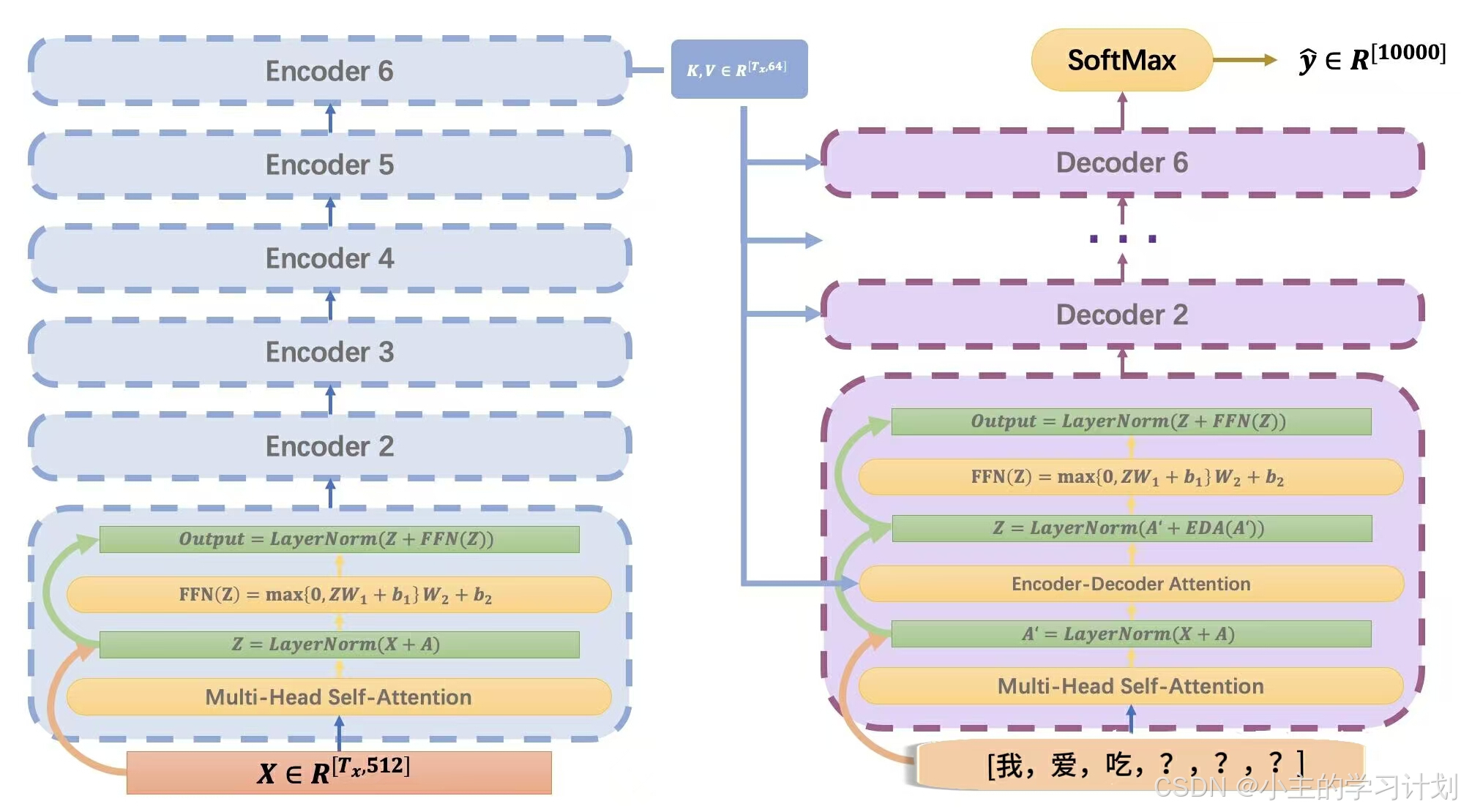
让我们仔细找找不同：看看上图右边的$Decoder$结构，熟悉的$LayerNorm$，熟悉的跳层连接，熟悉的叠加……这个$Encoder-decoderAttention$是什么？还有为什么左边的 $Encoder6$ 输出的是$K$和$V$？

当我们对输入序列经过6层$Self-Attention$的洗礼以后，第六层$Encoder$模块的输出 $A\in R[T,512]$中，每一个$Attention$值现在都对这句话有着相当高屋建瓴的理解。可能$A1$的意思是“这句话开头含有着一个雄性哺乳纲灵长目人科人属智人种的单数主语”，而$A2$的意思是“这句话中暗含着事件主体和事件客体之间微妙的互相包含关系”…总之如果现在$DecoderTransformer$想要知道译文的第 i 个词语该输出什么，直接去问问$Encoder6$再好不过了。

于是我们首先把Encoder 6输出的$A\in R[T,512]$乘以$W_k$和$W_v$得到矩阵$K、V\in R^{[T,64]}$。然这里的$W_k$和$W_v$ , 在$A$输入不同层的decoder时是不一样的。
那么问题来了，既然$K$ 和$V$ 已经通过计算得出，那么矩阵$Q$在哪呢？其实，Encoder-decoder Attention发出的问题 $Q$ 来自其本身Decoder模块中上一层的输出。

当然，$Encoder-decoderAttention$本身也是一个$MultiHead-Attention$。简单来说，这个模块就是一个$MultiHeadAttention$，只不过它的 $Q$ 是来自于上一层$Multi-HeadAttention$的输出， $K$ 和$V$ 则来自$Encoder6$的输出。

最后，我们把$Decoder6$的输出全部输入进一个全连接神经网络中，并使用$SoftMax$激活函数输出当前这句话（比如“我爱吃香？？？”）的下一个词应该是应该是什么，这里的概率通过一个 $\hat{y}\in R^{[10000]}$表示，10000是我们的词汇表的大小。（如果这是个训练良好的网络，它可能会在“蕉”这个字对应的位置上输出最大的概率）。

相信你现在就可以毫不费力地看懂原文中的这个复杂的模型示意图了:

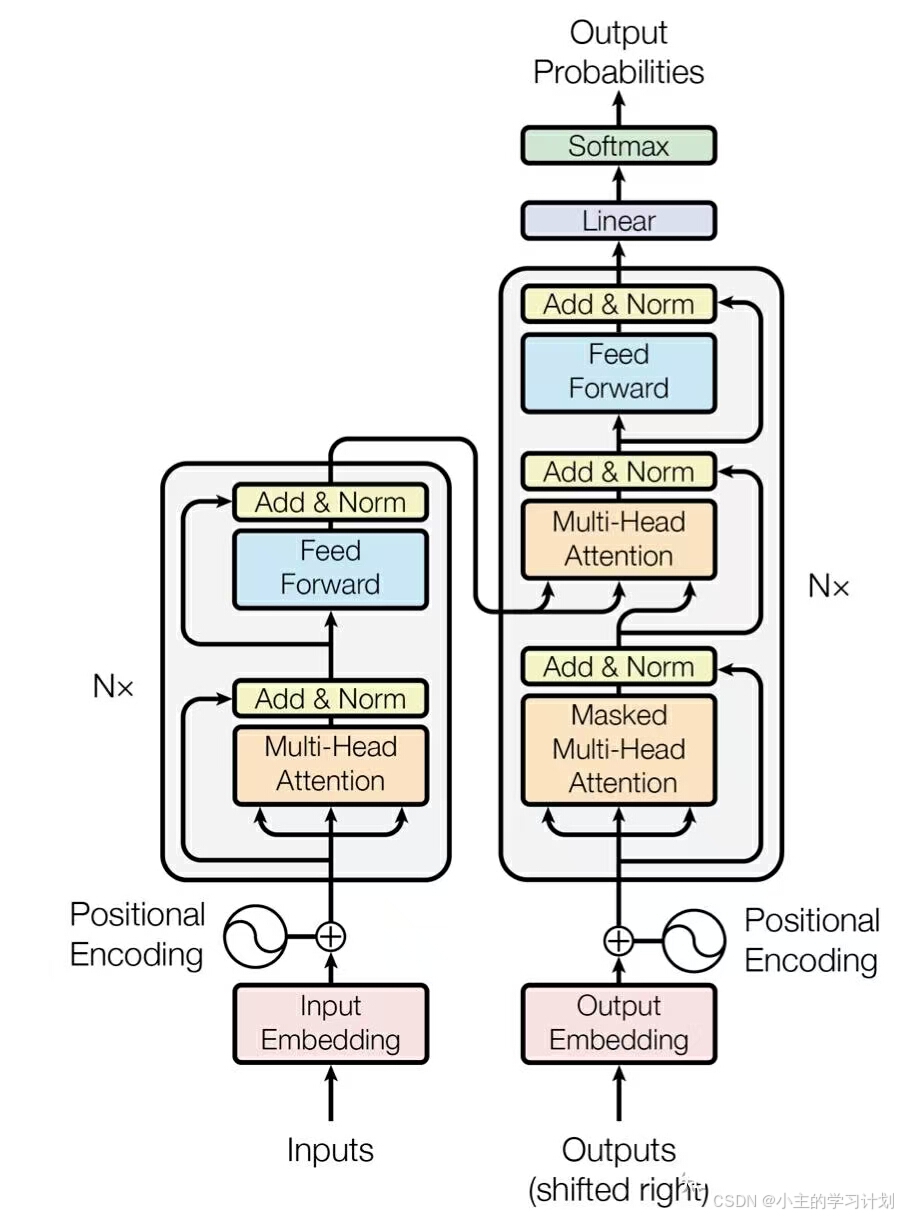
其他一些细节问题

我们已经知道了所有的模块是如何工作的，但是一个尚未解决的问题是：在最开始的时候，我们要往Decoder Transformer里输入什么？

答案是$？？？？？？？$

更准确来说，是$<SOS>？？？？？？？$

我们的网络还什么都不知道呢，输入任何东西都没什么意义，所以我们一开始就只能输入一个表示句子开始的Token让网络进行计算，网络这时候就需要输出第一个词的概率分布，也许它会输出一个"我"有着最大概率的概率分布。那么好，我们现在的输入就变成“我？？？？？”了。

接下来我们就把“$<SOS>$我？？？？？”再输入Decoder网络，得到新的下一个词的概率分布，也许“是”这个词此时有着最大的概率，那么我们的下一次输入给Decoder网络的内容就是“$<SOS>$我是$？？？？$”了。我们就一直这样循环下去，直到某一次输出中"$<EOS>$"（End of Sentence）有了最大的概率，我们就认为这段输出算是到头了。

值得注意的是，在不断向Decoder网络输入句子时，我们的Encoder网络就不需要再运行了，在处理一句话的过程中，Encoder网络只需要在最开始运行一次。

你可能会问：我们为什么不只输入“$<SOS>$我是”到网络中，而输入“$<SOS>$我是$？？？？$”到网络中呢？很遗憾，我们的Transformer不能处理任意长度的输入，对于Decoder网络和Encoder网络，我们都只能输入一个固定长度的句子，不同的句子长短不一，我们就向短的句子的末尾加入无意义的占位符延长到统一长度。

导师驱动（Teacher forcing）训练

相比于在传统的循环神经网络中输出一个单词需要上一个单元的隐藏层值，Transformer的每一个输出都只依赖于已经输出的序列和Encoder网络的隐藏层输出。如果想加速传统循环网络的训练，我们没什么好办法——因为上一个单元的隐藏层值可没什么投机取巧的算法，只能乖乖一个个算。但是Transformer不一样，我们可以不使用Decoder网络输出的前几个词语，而直接使用正确答案$y$中的对应词语，来计算第 $i$个输出词。

这个正确答案就像老师一样，在网络考虑如何输出第$i$个词时，老师保证前 $i-1$个词全都是完美的正确答案，这样网络就可以更好的学习如何输出这第$i$个词，而不用担心之前犯下的错误。当然，更重要的是，我们现在可以同时计算网络的每一个输出词，大大提高了训练速度，事实证明，这种导师驱动训练可以达到很好的效果。

位置编码

最后一步啦！！！

我们计算Self Attention的式子是：$A={\alpha }_1{V}_1+{\alpha }_2{V}_2+\dots \dots +{\alpha }_{Tx}{V}_{Tx}$。在$A$的眼里，$V_1,V_{10}$ 的地位是完全一样的，先后顺序无法体现在Transformer中。

但是在自然语言处理任务中，词语在句子中的位置是含有非常丰富的信息的。因此Transformer需要想个办法向模型中输入词语的位置信息。这里使用的方法就叫做位置编码（Positional Encoding）。

我们首先要知道位置编码往哪里输入，在transformer的实现中，如果我们的输入向量$X_{pos}$的大小为$[1,512]$，那么我们会根据$X$在这个句子中所处的位置计算出一个位置编码向量$P_{pos}\in R^{[1,512]}$。然后把它们直接相加，代替原来的$X_i$输入网络。

接下来我们要了解一下如何计算 $P_{pos}$：

现在假设我们的$X$是输入句子中的第$pos$个词语，而$X_k$表示向量$P_{pos}$的第$k$个元素，那么我们的位置编码就是按照如下规则产生的：

其中$d$代表$P$的总长度，在这里为512。这个公式在干什么？我们可以看到的是，对于一个单词的$P$，它的每一位的值就是在不同的周期的三角函数上取到的函数值，我们可以这样取出每一个单词的位置编码：

这张图可能没有那么好理解，但它确实很好的反映了我们的位置编码的取值方式。如果我们把所有的位置编码都放在一张图上我们可以看到如下效果：

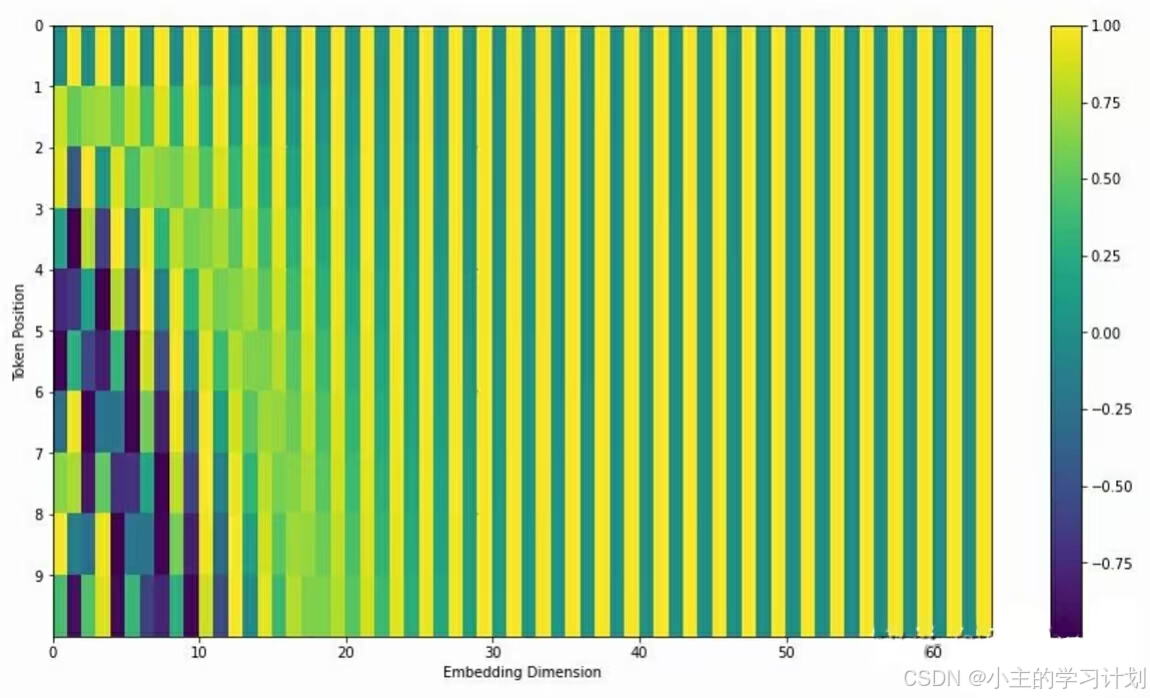
这里的每一行都代表着某一个词语的位置编码的可视化结果。可以看到，不同位置的词语有着独特的编码纹理规律，这使得网络能够区分出不同的词语位置。

那么为什么位置编码好使呢？
假设逆正在阅读"The animal didn’t cross the street because it was too tired"的第一层Self-Attention层。现在你读到了"it"，你很好奇这个“it”指代什么，于是你生成了一个 $Q$，尝试去找到答案。

你现在需要使这个$Q$和名词性的$E$更加相似，因为这样你的$Q$才更可能和正确答案$K$产生更大的乘积 $Q{K}^T$。

结果“Street”和“Animal”都找上你了，你很困惑，到底哪个才是“it”所代表的呢？丰富的经验再次告诉你：一般来说句首的那个名词会有更大的概率在后面的内容中以“it”指代。于是你翻开了一本“PE”字典：

这本字典上很清楚写着句子中的第一个词有着怎样的激活规律，于是你把Q根据第一条PE的纹理移动了一些，由于：

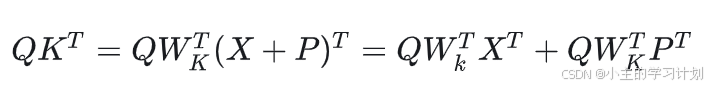
于是句首词语现在能够有更大的$Q{W}_K^T{P}^T$，你再次询问所有的$K$，现在只有“The Animal”脱颖而出了。你非常的快乐，把“Animal”赋予一个较高的权重上交给FFN了。