Good Key, Bad Key（CF1703G）题解

题面

时间限制 $1s$ | 空间限制 $256M$

链接在这里

题目描述：

你有 $n$ 个箱子。第 $i$ 个箱子中有 $a_i$ 个硬币。你需要按照从箱子 $1$ 号到箱子 $n$ 号的顺序打开所有 $n$ 个箱子。
你可以用以下两种钥匙之一打开一个箱子：

• 好钥匙：使用一次消耗 $k$ 个硬币。
• 坏钥匙：使用时不消耗硬币，但会使所有未打开的箱子中的硬币数减半（包括正要打开的这个箱子）。硬币减半时向下取整。比如，用坏钥匙打开箱子 $i$ 号时，$a_i=a_i/2$，$a_{i+1}=a_{i+1}/2$，$......$，$a_n=a_n/2$。
  所有钥匙用过一次就会断掉（别想着买一把好钥匙开完所有箱子了），好钥匙需要重复付费，坏钥匙效果会重复计算。
  也就是说，你总共需要使用 $n$ 把钥匙，每个箱子用一把。开始时，你没有硬币和钥匙，如果想用好钥匙，你就得去买。值得注意的是，在这个过程中你可以赊账买钥匙；例如，如果你只有 $1$ 个硬币，你也可以购买价值 $k=3$ 个硬币的好钥匙，你的余额会变成 $-2$ 个硬币。
  你需要求出开完所有箱子之后你能获得的最大硬币数量（显然大于等于 $0$ ）。

输入格式：

第一行包含一个整数 $t$（$1\le t\le 10^4$），表示测试数据的组数。

• 每组测试数据的第一行包含两个整数 $n$ 和 $k$（$1\le n\le 10^5$，$0\le k\le 10^9$），分别表示箱子的个数和每把好钥匙的花费。
• 每组测试数据的第二行包含 $n$ 个整数 $a_i$（$0\le a_i\le 10^9$），表示每个箱子中硬币的数量。
  所有测试数据中 $n$ 的总和不超过 $10^5$ 。

输出格式：

对于每组测试数据，输出对应的可获得的最大硬币数量。
提示（题面中给出）：开 $long$ $long$

样例输入输出：

样例1输入	样例1输出
5 4 5 10 10 3 1 1 2 1 3 12 10 10 29 12 51 5 74 89 45 18 69 67 67 11 96 23 59 2 57 85 60	11 0 13 60 58

样例解释：

• Buy a good key for $5$ coins, and open chest $1$ , receiving $10$ coins. Your current balance is $0+10-5=5$ coins.
• Buy a good key for $5$ coins, and open chest $2$ , receiving $10$ coins. Your current balance is $5+10-5=10$ coins.
• Use a bad key and open chest $3$ . As a result of using a bad key, the number of coins in chest $3$ becomes $\lfloor \frac{3}{2}\rfloor =1$ , and the number of coins in chest $4$ becomes $\lfloor \frac{1}{2}\rfloor =0$ . Your current balance is $10+1=11$ .
• Use a bad key and open chest $4$ . As a result of using a bad key, the number of coins in chest $4$ becomes $\lfloor \frac{0}{2}\rfloor =0$ . Your current balance is $11+0=11$ .
  At the end of the process, you have $11$ coins, which can be proven to be maximal.

题解：

思路

本题可以使用贪心的思路

如果现在有 $i$ 把好钥匙，考虑怎样使用这些好钥匙。

因为原始箱子里硬币数量的和是固定的，使用坏钥匙会对后面所有的箱子产生影响，所以越先使用坏钥匙对箱子里硬币总数的影响越大。

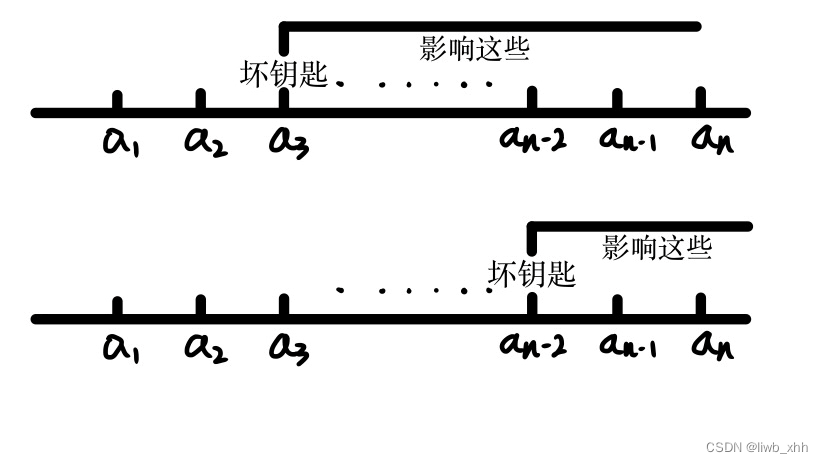
贪心想法：先使用 $i$ 把好钥匙，剩下的使用坏钥匙。

实现

• 发现好钥匙部分就是再求 $a_1+a_2+...+a_n$ 的值可以使用前缀和优化
• 坏钥匙部分的除数每次乘以$2$增加速度很快，暴力解决
• 记得开longlong（题目中有提示）

参考代码：

#include<bits/stdc++.h>
#define LL long long
using namespace std;

LL a[100010],sum[100010],n,k,t,ans,mx;

int main()
{
	cin >> t ;
	while(t--)
	{
		cin >> n >> k ;
		for(int i=1;i<=n;i++)
			cin >> a[i] ;
		ans=0;//ans存储结果
		mx=0;//mx存储最大硬币数
		sum[0]=0;//前缀和数组
		for(int i=1;i<=n;i++)
		{
			mx=max(a[i],mx);
			sum[i]=sum[i-1]+a[i];
		}
		for(int i=0;i<=n;i++)//枚举有i把好钥匙
		{
			LL cnt=1,anss=sum[i];
			for(int j=i+1;j<=n;j++)
			{
				cnt*=2;//cnt记录除数
				if(cnt>mx)
					break;//除数大于最大值时结果全部为 0，不用计算
				anss+=a[j]/cnt;
			}
			anss-=i*k;
			ans=max(ans,anss);
		}
		cout << ans << endl ;
	}
	return 0 ;
}