最大最小距离算法（Max-Min-distance）

基本思想：

对待分类模式样本集采取以最大距离原则选取新的聚类中心，以最小距离原则进行模式归类。

算法原理和步骤：

1.从$N$个样本集中的任选取一个样本，作为第一个聚类中心$z_1$；
2.选取距离第一个聚类中心$z_1$最远的样本作为第二个聚类中心$z_2$；
3.计算其余样本与$z_1、z_2$之间的距离，并求出它们中的最小值，即：
$$d_{ij}=\Vert x_i-z_j\Vert ,j=1,2$$
$$d_i=min[d_{i1},d_{i2}],i=1,2,...N$$
4.若：($\theta 为选定的比例系数$)
$$d_l=\underset{i}{\max }[min[d_{i1},d_{i2}]]>\theta \ast \Vert z_1-z_2\Vert$$
则相应的样本$x_l$作为第三个聚类中心$z_3$,转至下一步继续判断是否存在新的聚类中心，否则转至第六步；
5.假设存在$k$个聚类中心，计算各样本到各个聚类中心的距离$d_{ij}$，并算出：
$$d_l=\underset{i}{\max }[min[d_{i1},d_{i2},...,d_{ik}]]>\theta \ast \Vert z_1-z_2\Vert$$
若成立，则$z_{k+1}=x_l$,并循环此步骤，继续判断是否有新的聚类中心存在，否则转至第六步；
6.当判断不再有新的聚类中心存在时，将样本集按最小距离原则分到各类中去，即计算：
$$d_{ij}=\Vert x_i-z_j\Vert ,j=1,2,...,k,i=1,2,...,N$$

MATLAB代码实现：

clear all
close all
clc
%坐标点，初始化选定比例系数
num = 10;eta = 0.5;
axis([0 10 0 10]);
hold on
%c = zeros(10,1);z = zeros(10,2);
x1 = [0,0];x2 = [3,8];x3 = [2,2];x4 = [1,1];
x5 = [5,3];x6 = [4,8];x7 = [6,3];x8 = [5,4];
x9 = [6,4];x10 = [7,5];
W = [x1;x2;x3;x4;x5;x6;x7;x8;x9;x10];
%% step1 任选一个坐标点作为第一个聚类中心z1
R= randperm(num);
c(1) = R(1);
z(1,:) = W(c(1),:);
%% step2 从数据中选取一个距离z1最远的坐标点，作为第二个聚类中心z2
d = zeros(num,1);
for i = 1:num
    d(i) = norm(z(1,:)-W(i,:));
end
[~,c(2)] = max(d);%距离，位置
z(2,:)= W(c(2),:);
%% step3 计算剩余数据与z1,z2之间的距离，并求其最小距离
d =zeros(num,2);
for i = 1:num
    d(i,1) = norm(z(1,:)-W(i,:));
    d(i,2) = norm(z(2,:)-W(i,:));
end
D = zeros(num,1);
for i = 1:num
    D(i) = min(d(i,:));
end
%% step4 确定是否存在第三个聚类中心
[m,n] = max(D);%最大值，位置
if m>eta*norm(z(2,:)-z(1,:));
    c(3) = n;
    z(3,:) = W(c(3),:);
    jump = 1;%转至step5
else
    jump = 2;
end

switch (jump)
    case 1
        k = 4;
        %% step5 继续确定是否存在聚类中心
        for p = 1:num
            d =zeros(num,length(c));
            for i = 1:length(c)
                for j = 1:num
                    d(j,i) = norm(z(i,:)-W(j,:));
                end
            end
            for i = 1:num
                D(i) = min(d(i,:));
            end
            [m,n] = max(D);%最大值，位置
            if m>eta*norm(z(2,:)-z(1,:));
                c(k) = n;
                z(k,:) = W(c(k),:);
                k = k+1;
            else
                break  %没有新的聚类中心
            end
        end
        
    case 2
        break
end
%% step6 最小距离法进行分类
%首先计算数据到每个聚类中心的距离
D =zeros(num,length(c));
for i = 1:length(c)
    for j = 1:num
        D(j,i) = norm(z(i,:)-W(j,:));
    end
end
%归类，判断坐标点属于的类别
k = zeros(length(c),1);
for i = 1:num
    [m,n] = min(D(i,:));
    k(i,1) = n;%归类标识
end

%设置颜色
colour = zeros(length(c),3);
for i = 1:length(c)
    colour(i,:) = rand(1,3);
end

for i = 1:length(c)
    v = find(k == i);%位置
    u = length(v);%个数
    M = zeros(u,2);%用来存储所属同一类的点
    for j = 1:u
        M(j,:) = W(v(j),:);
    end
    P = plot(M(:,1),M(:,2),'<');
    set(P,'color',colour(i,:));
end

结果：

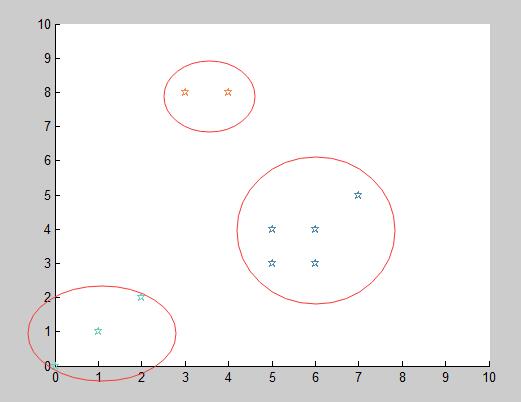
分析：

这种算法聚类结果与选取的第一个聚类中心以及选定的比例系数 $\theta$ 有关。这会导致聚类结果不理想，所以个人认为要尽可能避免聚类结果不理想的问题，首先可以找到距离原点最近的一点作为初始的聚类中心，同时 $\theta$ 大小根据样本的分布及 $\Vert z_1-z_2\Vert$ 的大小进行综合确定。